Today I Learn📖
- 큐 (강의)
- 해시 테이블 (강의)
- 그래프 (강의)
큐 (Queue)
=> 선입선출, 빼는 것(DeQueue), 맨 앞(Front), 맨 뒤(Rear), 넣는 것(EnQueue)
종류는 선형 큐(Linear Queue) / 환형 큐(Circular Queue)
선형 큐 (Linear Queue)
- 선형 큐 구현 방법
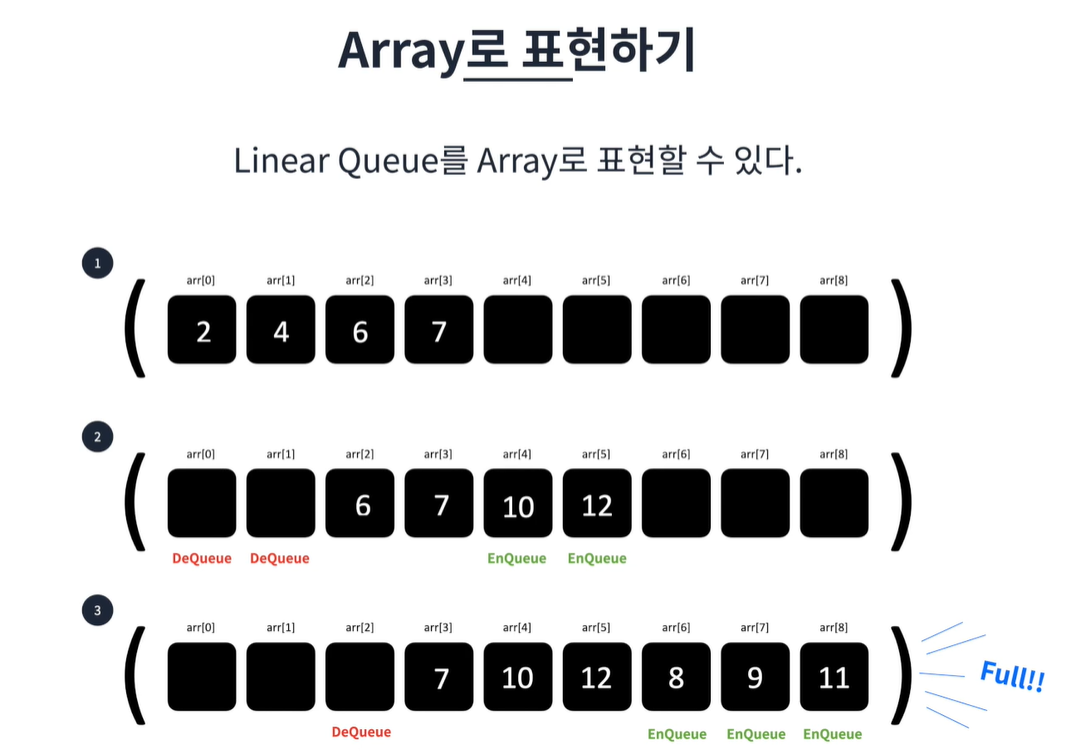
- 배열: 앞에서부터 뒤로 계속 추가하면 됨 (뺄 때는 앞에서부터 빼지만 빈 공간은 생김)
=> 방법이 간단해서 코테에서 풀 때 추천 !
js는 배열 증감이 유동적이라 배열이 꽉 차진 않지만, 빈 공간이 있으면 프론트 & 리어 인덱스 값이 무한정 커짐 -> 빈 공간을 앞당기면 선형시간 소요됨 ㅠㅠ
=> peek: 맨 앞 값 알아내는 함수
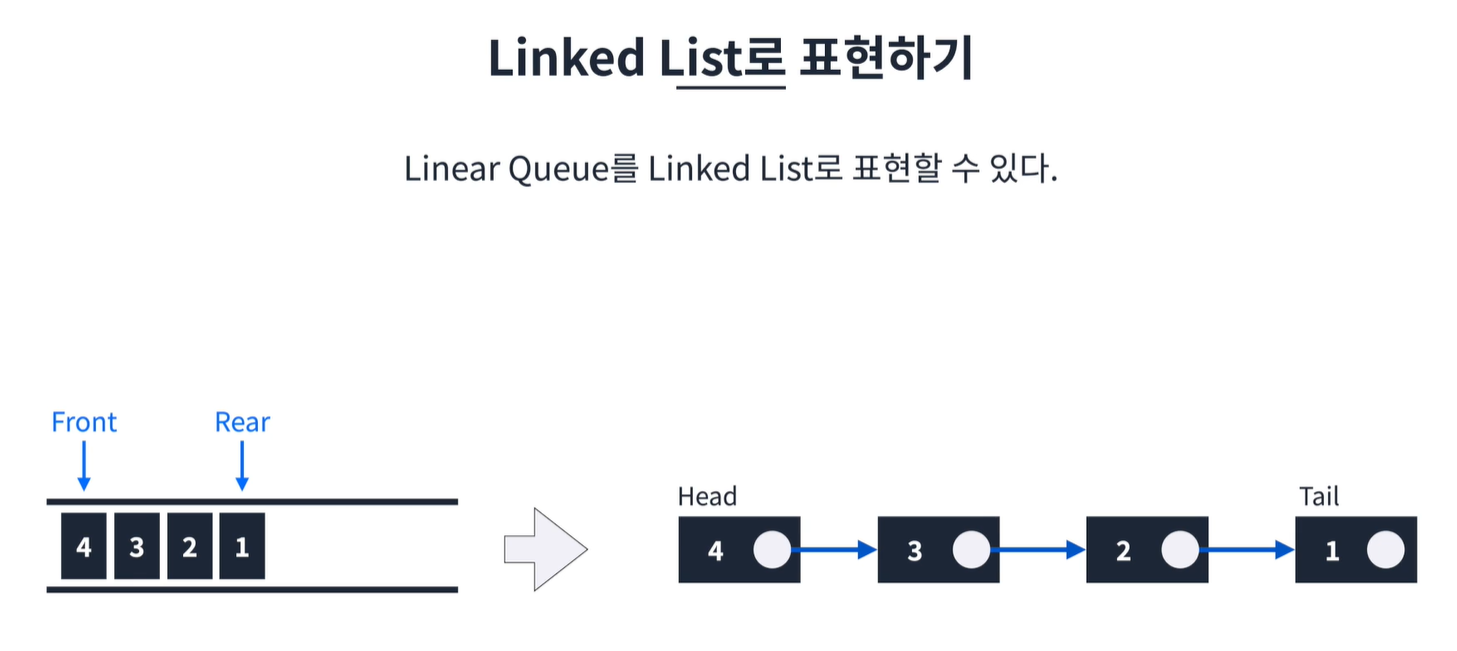
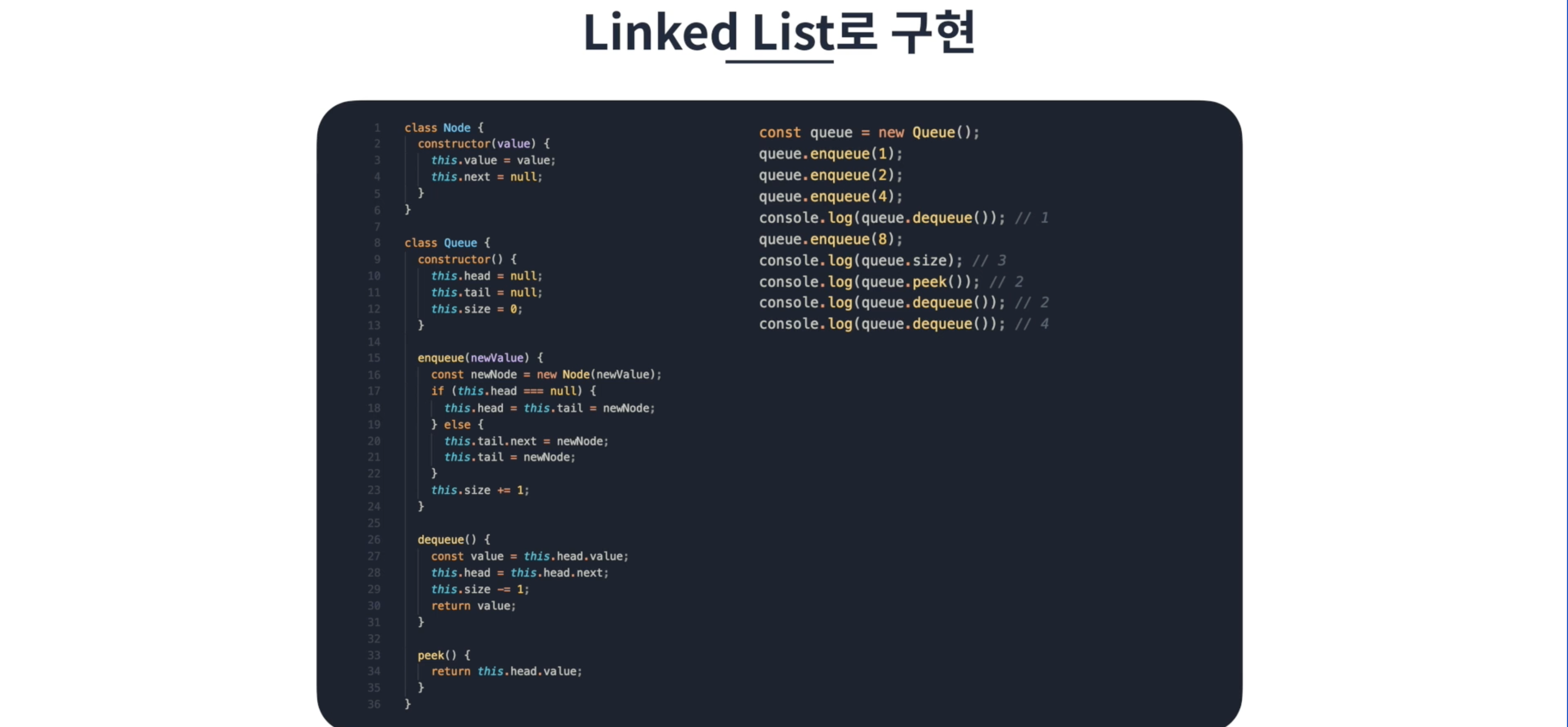
- 연결 리스트: 헤드 = 프론트, 테일 = 리어 역할. 인덱스 고민 없어짐
- 큐 구현 할 때 shift 쓰지 말기!! (선형시간 걸려서 수행시간 오래걸림 ㅠㅠ)
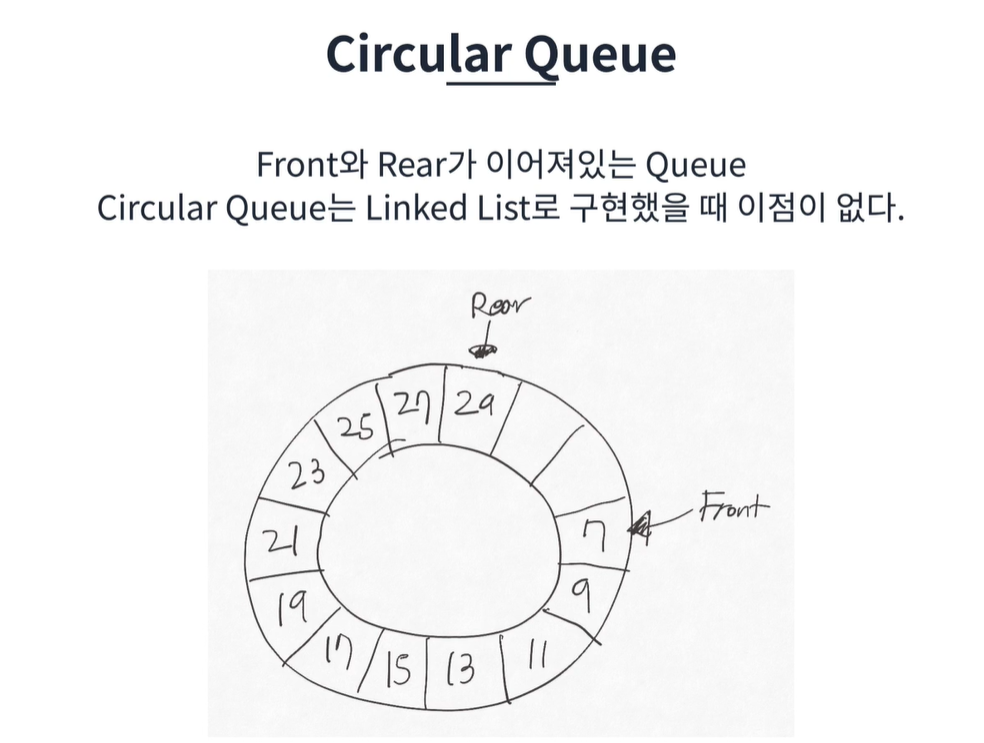
환형 큐 (Circular Queue)
=> 한정된 공간을 효율적으로 이용하는 것이기 때문 !
- 환형 큐 구현 방법
-> js에서 굳이 환형큐를 사용해야하는 상황은 많지 않으므로 외울 필요는 없음
- 배열
선형큐 코드와 비슷하지만 차이는 존재함 !
1. maxSize 받아서 큐 크기 제한
2. 리어/프론트가 크기를 벗어나면 다시 0번 인덱스부터 시작!
3. isFull 함수 생성해서 무한정 엔큐 되는 것 막기
해시 테이블
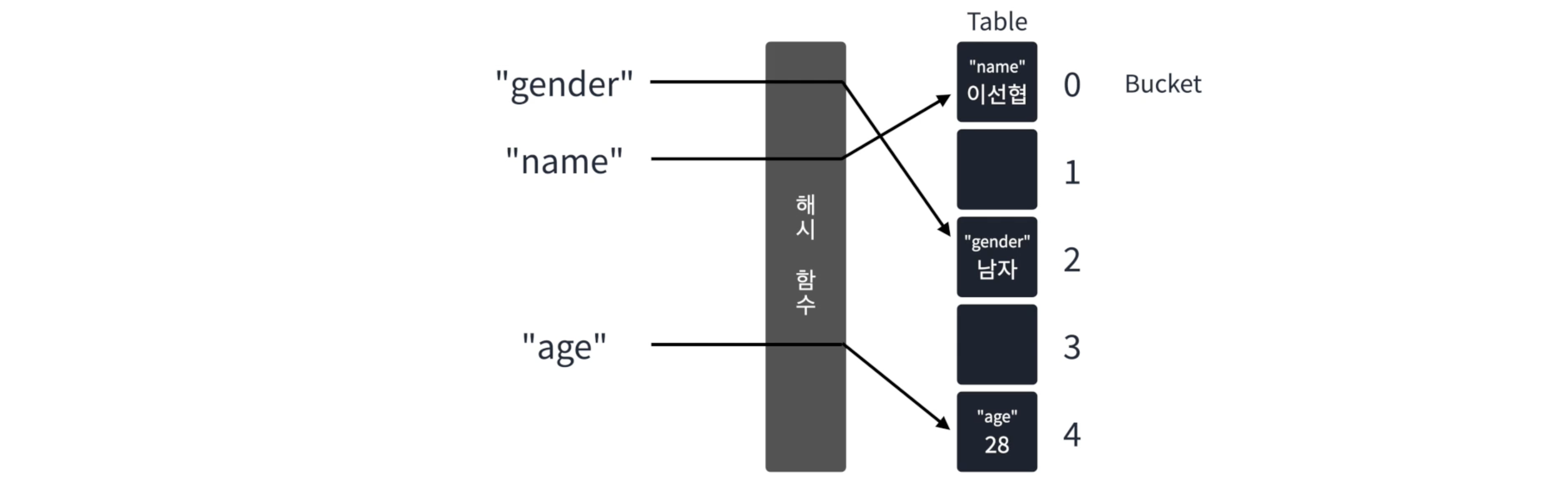
키와 값을 받아, 키를 Hashing(해싱)하여 나온 idx에 값을 저장하는 자료구조
-> key를 idx로 변환해 값을 넣는 것 => 마치 학교 사물함~
=> 삽입은 상수시간 소요, 키를 알고 있을 경우에는 삭제 & 탐색도 상수시간 소요
Table의 각 요소에는 키, 값을 모두 저장하고 있어야함- 각 테이블에 해당하는 idx를
Bucket이라고 부름
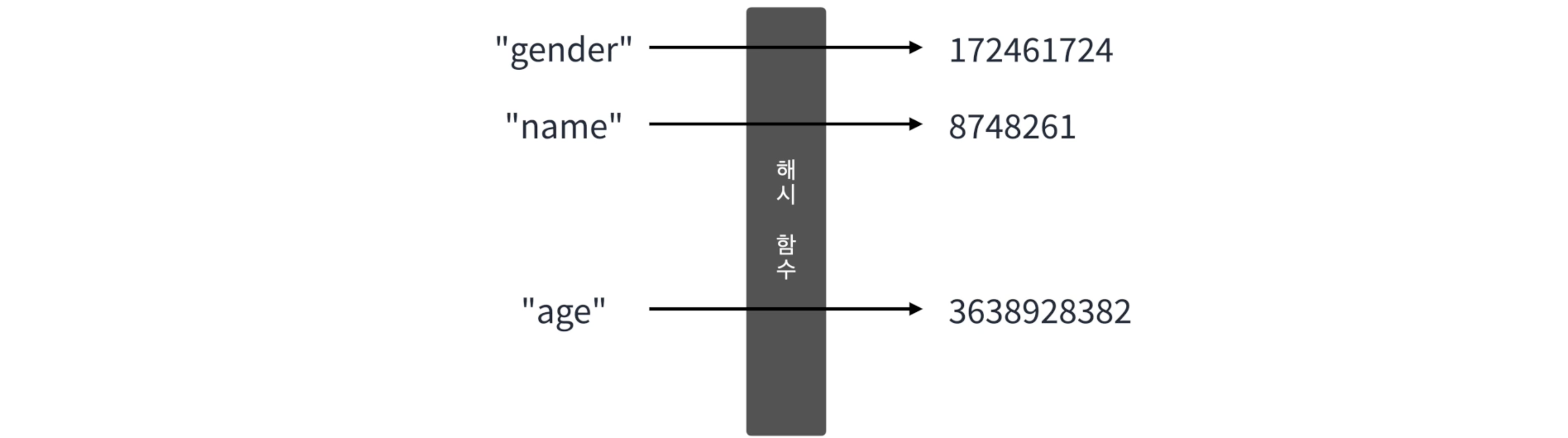
- Hash(해시): 입력받은 키를 잘게 잘라 숫자로 만드는 것
- Hashing: 데이터를 고정된 길이의 유일한 값으로 변환하는 과정, 해시 함수를 통해 진행함
- 해시 함수: 입력받은 값을 특정 범위 내 숫자로 변경하는 함수
-> 해시 함수는 특정한 구현 방식 존재 x
=> 해시 값은 마음대로 정하는 것 ! (문자열의 아스키 코드 값 모두 더하기 등, ...)
해시 테이블의 문제점 & 해결법
-
문제점: 해시 충돌(Hash Collision) 발생 가능
=> 해시 함수의 결과 값이 동일한 경우가 발생하는 것 (유일하지 않은 경우) -
해시 충돌 해결 방법 (4가지)
- 선형 탐사법: 충돌이 발생하면 idx를 옆으로 한 칸 이동시키기
-> 단순하지만 특정 영역에 데이터 몰릴 수 있음
-> 이동한 idx에서 또 충돌이 발생하면 충돌 안 할 때까지 계속 옆으로 가야함 => 최악의 경우 탐색에 선형시간 소요됨
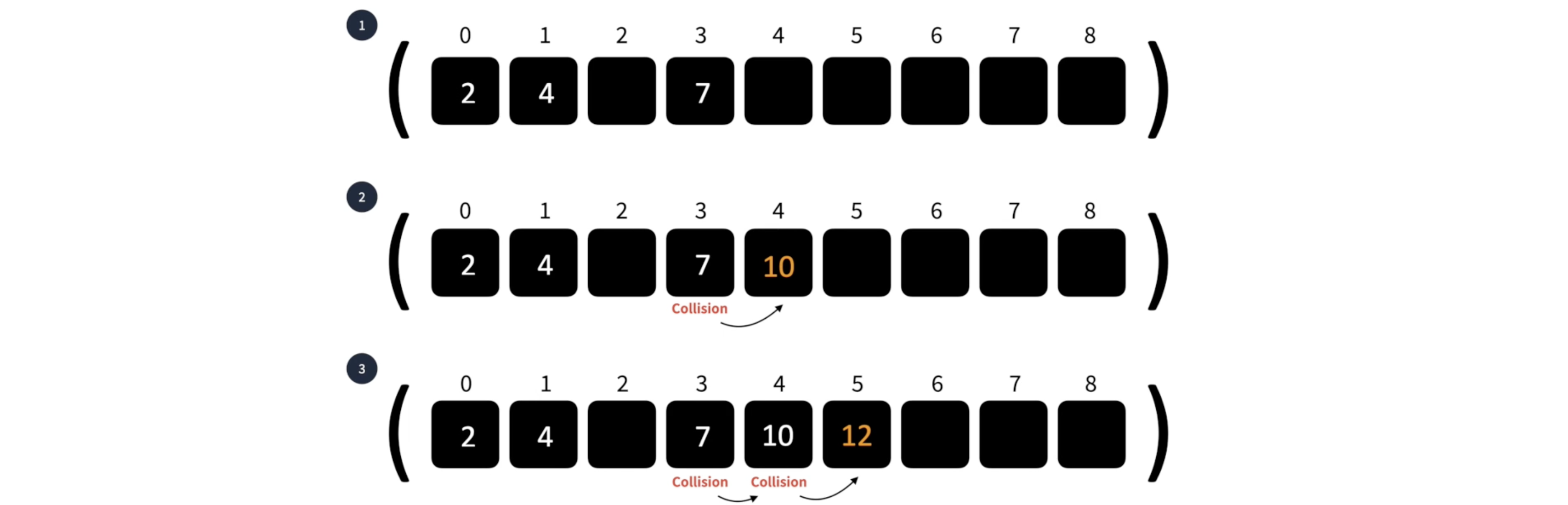
- 제곱탐사법: 충돌이 발생하면, 충돌 발생 지점에서 충돌 발생 횟수의 제곱만큼 idx 옆으로 이동
=> 제곱만큼씩 이동함(1번째 충돌은 1칸, 2번째 충돌은 4칸, ...)
-> 선형 탐사법보다는 특정 영역에 데이터 몰리는 것 방지
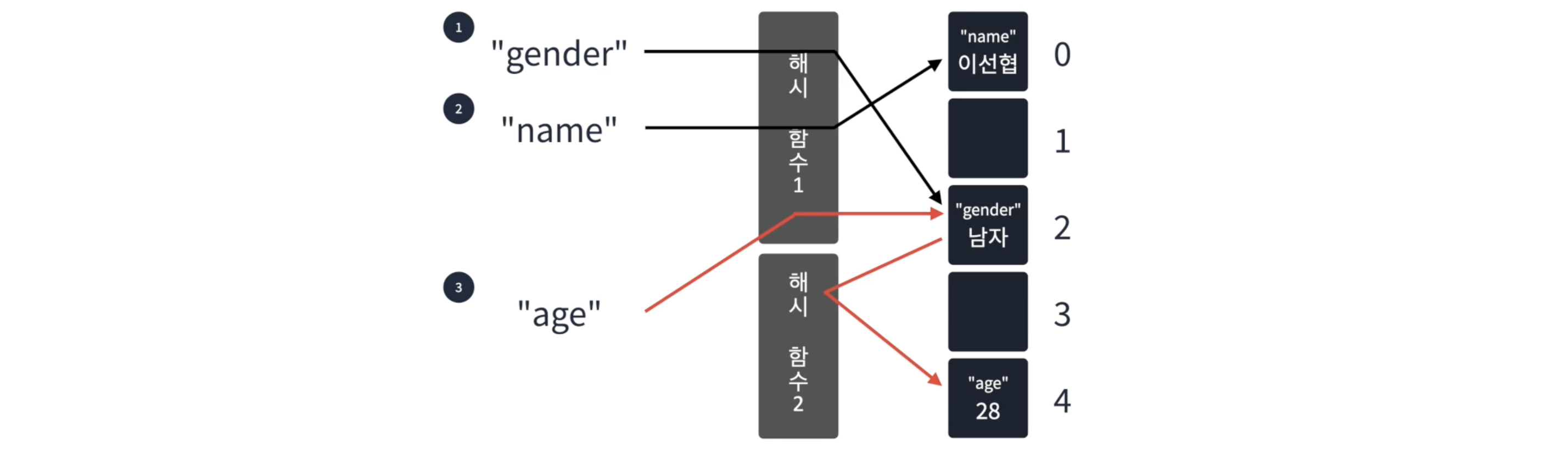
- 이중 해시: 충돌이 발생하면 기존 해시 함수 말고 2번째 해시 함수를 이용하는 것
-> 충돌이 발생하지 않을 때까지 만들어진 idx에서 2번째 해시 함수를 이용해 새로운 idx 계속 생성
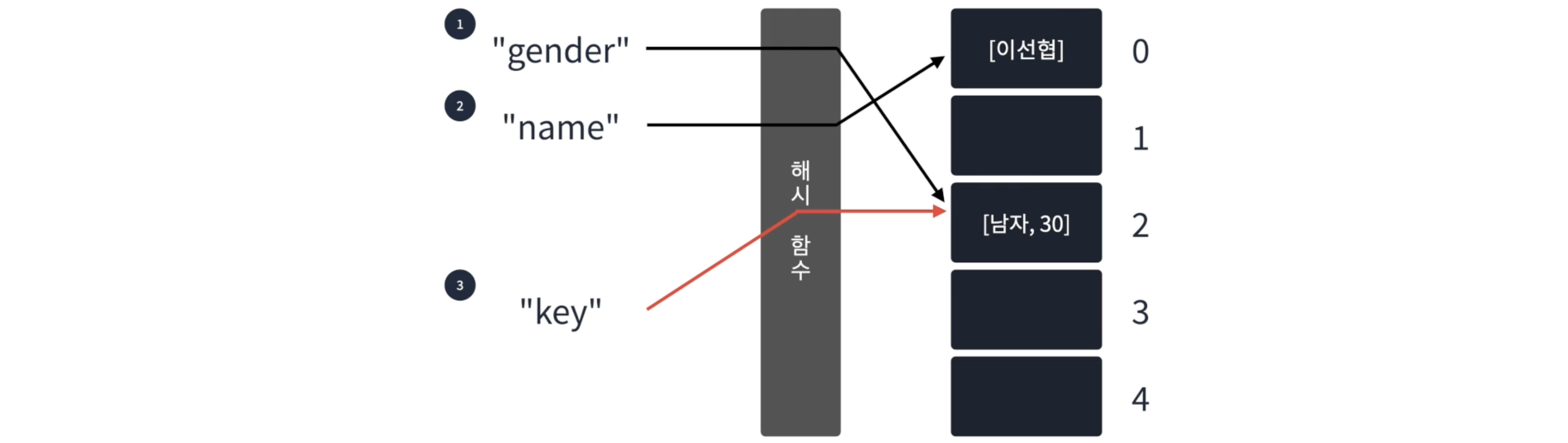
- 분리 연결법: 버킷의 값을 연결 리스트로 사용하며, 충돌이 발생하면 리스트에 값을 추가함
-> 충돌이 발생해도 다른 idx로 이동 안 함
-> idx를 리스트로 활용하여 그 뒤에 계속 값 추가하는 것 => 최악의 경우 하나의 버킷이 무한정 늘어날 수 있음
- 선형 탐사법: 충돌이 발생하면 idx를 옆으로 한 칸 이동시키기
-
해시 테이블은 값을 찾고 싶을 때 사용 !! (탐색)
-> 연결 리스트를 사용하면 선형 시간 소요되고, 배열도 idx를 모를 경우, 역시 선형시간 소요됨
=> 해시 테이블은 이름을 키로 사용하기 때문에 탐색, 삽입, 삭제가 상수 시간만에 끝남 (최악의 경우는 선형 시간 걸리지만 위에 2개 보다는 안정적임 ㅎ.ㅎ) -
js에서의 사용법
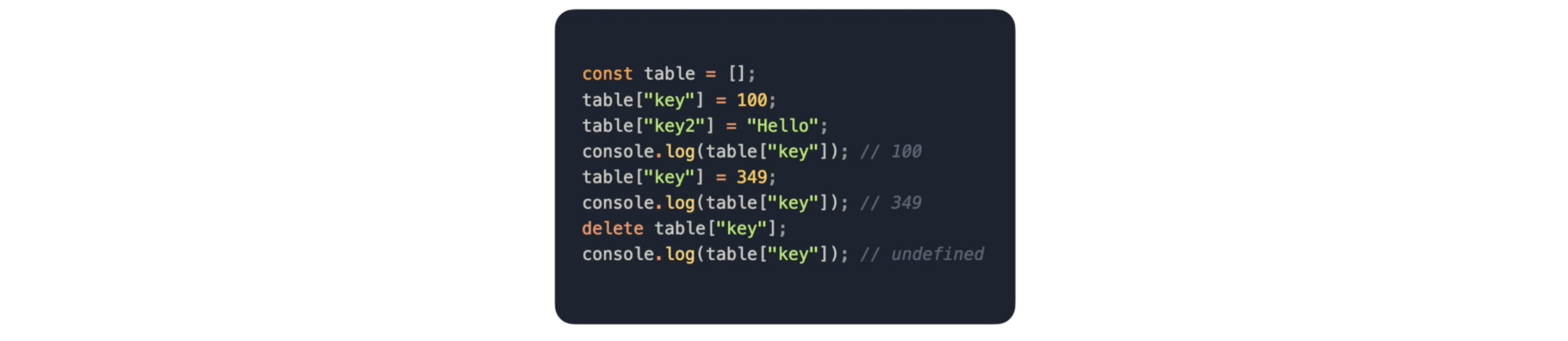
1. 배열을 직접 이용하기: js의 배열은 사실 객체라, 해시 테이블로도 쓸 수 있음
-> 올바른 사용방법이 아니기 때문에 비추천- 객체 사용: 가장 정석법
-> 들어오는 key값이 정수가 아니면 모두 문자열로 바꿔버림 (다양한 타입 사용 불가)
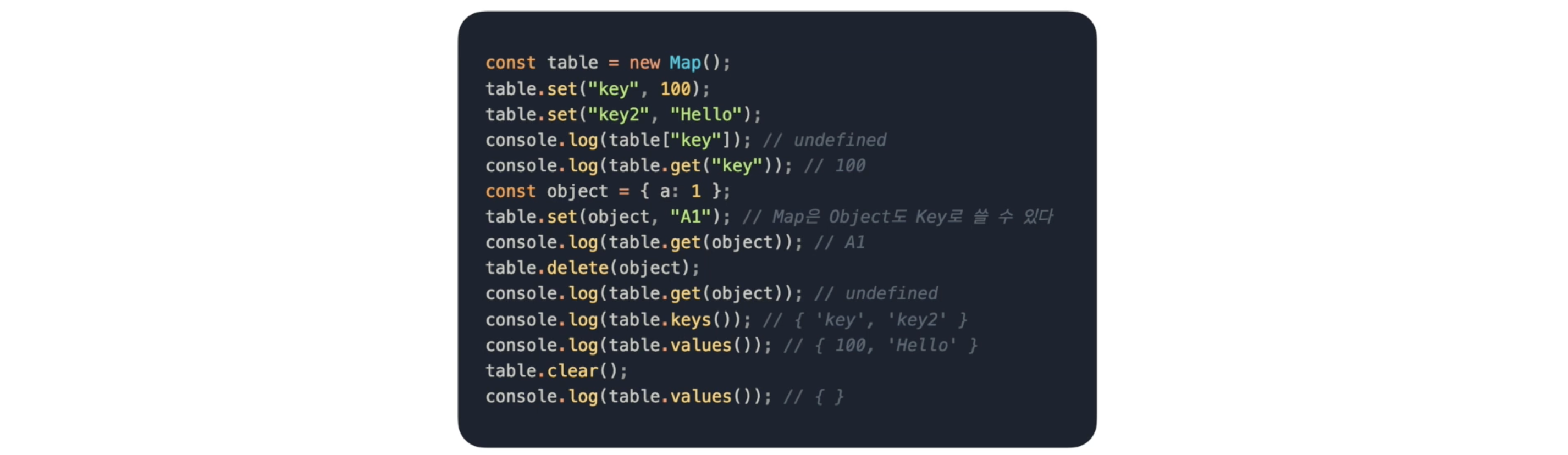
- Map
-> set, get 등 여러 메서드 제공 & 사용 가능, 순회하기도 편함
-> key값에 다양한 타입을 넣을 수 있음(오브젝트, 배열 등)
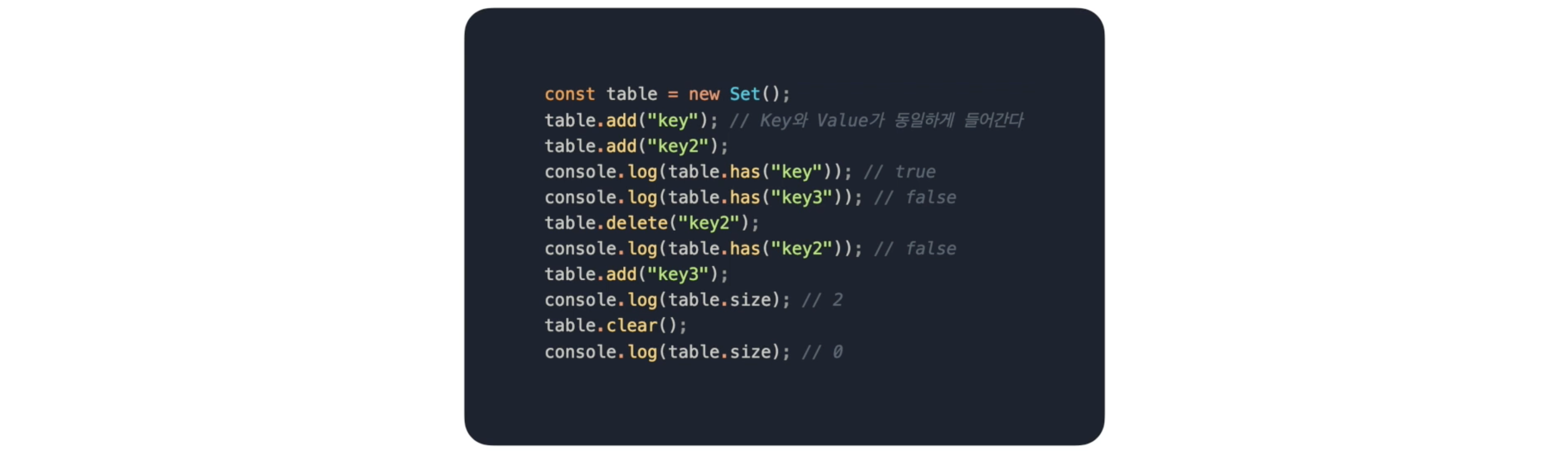
4.Set
-> 키 & 값이 동일하게 저장됨 (일종의 집합 연산)
-> 중복된 내용을 제거할 때 유용하게 사용 가능
- 객체 사용: 가장 정석법
그래프
정점 - 정점을 연결하는 간선으로 이루어진 비선형 자료구조
=> 정점(노드) 집합 + 간선(엣지) 집합으로 구성됨
- 특징
- 한 정점은 여러 개의 간선을 가질 수 있음
- 방향 그래프 / 무방향 그래프로 나누어짐
- 각 간선은 가중치를 가질 수 있음
- 사이클이 발생할 수 있음
- 사이클
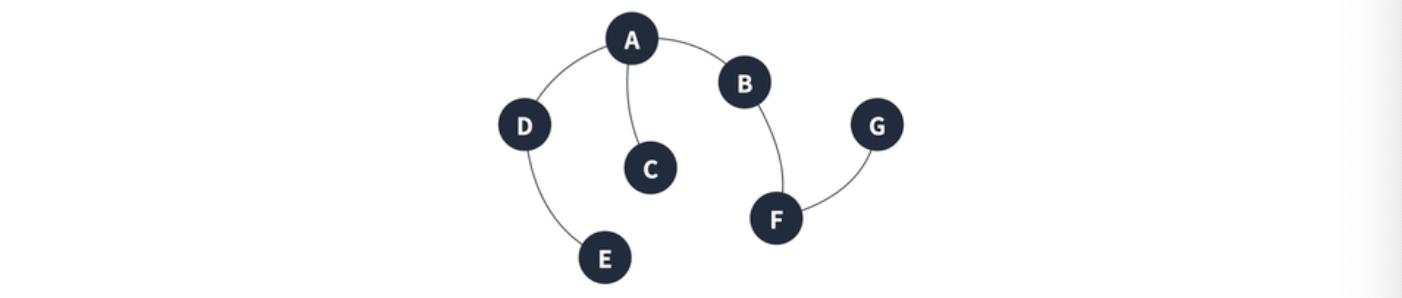
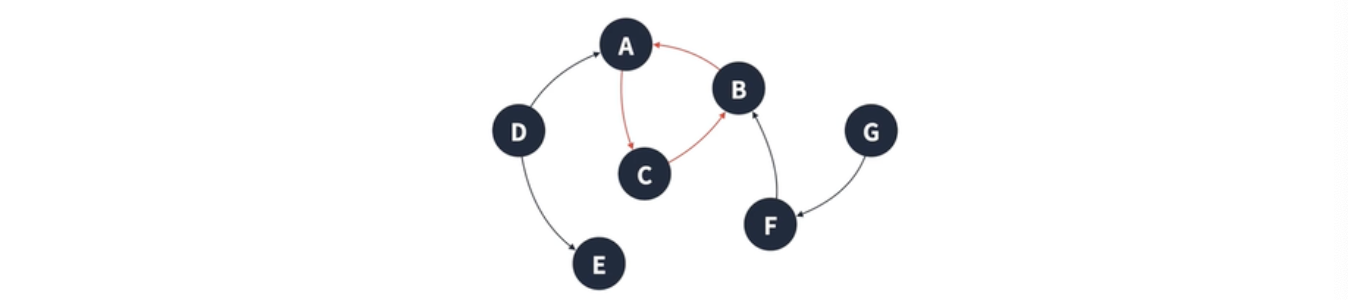
그래프의 정점과 간선의 부분 집합에서 순환이 되는 부분 (loop 도는 부분)
=> 다음 그림의<A, B, C>
방향성에 따른 그래프 분류
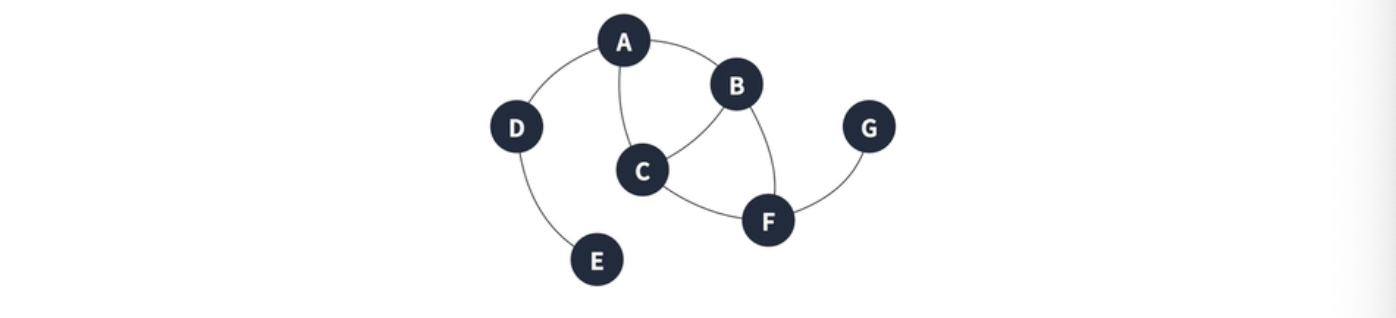
무방향 그래프
간선으로 이어진 정점끼리는 양방향 이동 가능 (간선에 방향 없음)
=>(A, B)와 (B, A)는 같은 간선
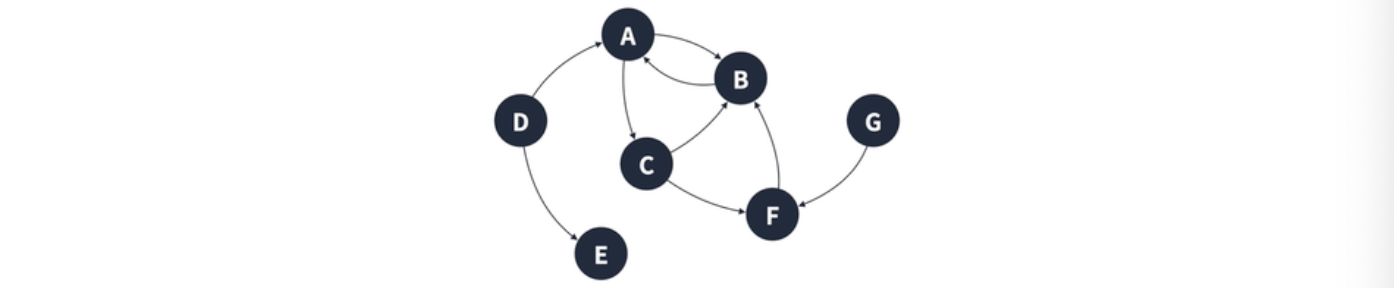
방향 그래프
간선에 방향성이 존재함
=><A, B>와 <B, A>는 다른 간선(서로 양방향 이동이 가능해도 다른 취급, 간선도 따로 있음)
연결성에 따른 그래프 분류
연결 그래프
모든 정점이 서로 이동 가능한 상태
비연결 그래프
특정 정점끼리는 간선이 없는 상태, 특정 정점은 하나의 간선도 없는 상태
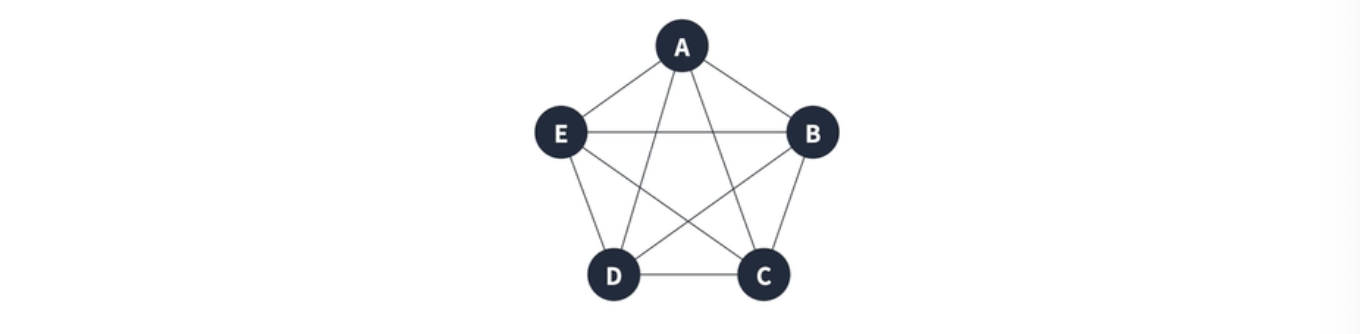
완전 그래프
모든 정점끼리 다 연결된 상태
=> 한 정점의 간선 수 = (정점 개수 - 1)
=> 모든 간선의 수 = (정점 개수 - 1) * 정점 개수
그래프 구현 방법
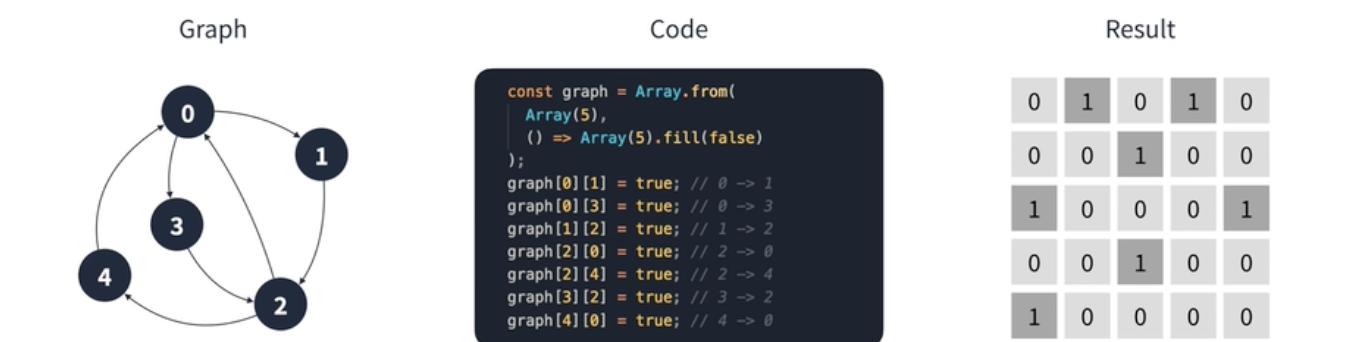
- 인접 행렬 => 2차원 배열
- 정점 수만큼 배열 만든 후, 연결 안 된 상태(false)로 초기화
- 행렬의
열 부분 = 시작 정점/행 부분 = 도착 정점으로 설정 -> true값을 주면 그 정점은 연결 된 것- 만약 간선에 가중치 주고 싶은 경우 => 불린값 대신
null & 가중치 값설정- 무방향 그래프인 경우, 모든 값을 대칭으로 넣기
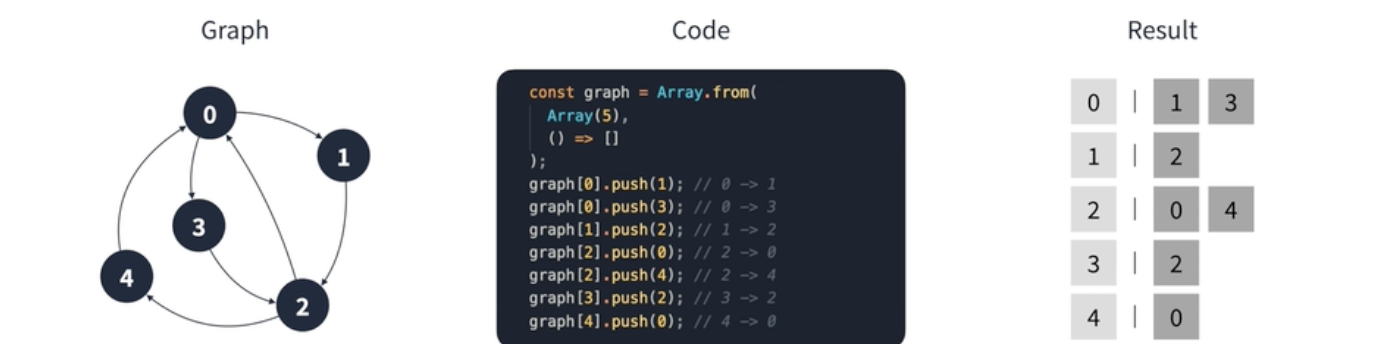
- 인접 리스트 => 연결 리스트
- 정점 수만큼 배열 만든 후, 연결할 정점을 배열에 추가하기
=> JS의 배열은 무한정 늘어날 수 있기 때문!
😊오늘의 느낀점😊
지금까지 큐 문제를 풀 때는 shift를 사용했는데, 이 방법이 선형시간을 소요해 효율성을 떨어뜨린다는 걸 배웠다.
사실 좀 충격이다.,, 다른 사람들 풀이에도 shift를 많이 썼길래 맞는 줄 알았다 ㅋㅋㅋㅋㅋ ㅠㅠ
이제부터 삭제가 필요할 땐 class로 구현하는 습관을 들여야겠다 !!
해시 문제는 정확하게 배운 적 없이 그저 Map, Set을 이용해 풀어왔는데 이번에 제대로 짚을 수 있어 좋았다 ㅎㅎ
dfs, bfs에서 사용되는 그래프는 어려워보여서 아직 시도해보지 않았었다. 이번과 다음번에 그래프를 학습해서 알고리즘에 적용해봐야겠다 !!