B+Tree Index

개발기록·2024년 7월 6일

CS

목록 보기

6/6

B+Tree Index File

데이터를 삽입 / 삭제 할 때 약간의 변경으로 데이터의 정렬을 보장한다 (주기적인 재정렬의 필요가 없다)
그러나, 삽입, 삭제 공간 오버헤드가 추가된다는 단점이 있다
하지만, B+트리의 장점이 단점을 극복할 정도로 좋기 때문에 많이 사용되는 구조이다

B+Tree는 몇가지 특성을 만족하는 Tree 이다

n은 B+Tree의 차수 즉, 각 노드의 포인터 개수를 의미한다
root 에서 모든 leaf 까지의 높이가 동일해야 한다
root와 leaf가 아닌 모든 노드는 n/2 ~ n 개의 child를 가져야 한다 (pointer)
leaf 노드는 (n-1)/2 ~ n-1 개의 값을 가져야 한다 (search-key)
특별 케이스
- 만약 root가 leaf가 아니라면 최소 2개의 children을 가져야 한다
- 만약 root가 leaf라면 0 ~ n-1개의 값을 가져야 한다

B+Tree Node 구조

$K_i$ 는 search-key 값이다
$P_i$ 는 children을 가리키는 pointer 혹은 레코드를 가리키는 pointer들 이다.
search-key는 작은 값 부터 오름차순으로 정렬되어 있다
Non-leaf 노드에서는 각 key를 가리키는 pointer는 오른쪽에 위치한다 (가장 왼쪽 포인터를 고립)
leaf 노드에서는 각 key를 가리키는 pointer는 왼쪽에 위치한다 (가장 오른쪽 포인터를 고립)
key에 해당하는 값보다 크면 오른쪽 key로 이동하여 자신 보다 큰 key를 만나면 해당 key의 왼쪽 포인터로, 자신과 같거나 작은 포인터를 만나면 오른쪽 포인터로 이동한다
n = 6인 B+Tree
leaf 노드의 key 개수는 3~5 사이어야 한다
root와 leaf가 아닌 노드는 3~6개의 child를 가진다
root는 최소 2개의 children을 가진다

B+Tree Observation

non leaf 노드는 결국 sparse index를 형성하는 형태이다
B+tree는 높이가 매우 낮다
- root는 최소 2개의 자식을 가져야 한다
- 그 아래는 노드들으느 최소 (n/2)개의 자식을 가져야 하니 총 2*(n/2)개의 key
- 또 그 아래는 2*(n/2)*(n/2) ....
- 총 K개의 serach-key가 존재할 때, 높이는 $log_{(n/2)} K$ 를 넘지 않는다
- n 값을 100 이상의 큰 값을 사용하기 때문에 효율적이다
삽입 / 삭제 알고리즘 또한 로그 시간 내로 해결이 가능하다
Non-unique key를 사용하는 경우, bucket이 필요하다. 하지만, 이 방법은 구현이 어려워 보통 키를 unique하게 만들 수 있는 uniquifier를 사용한다

B+Tree Insertion

leaf node에서 serch-key가 들어갈 자리를 찾는다
2-1. 자리가 있는 경우 넣는다
2-2. 자리가 없는 경우 split (n/2개만 남기고 새로운 노드에 넣는다)
2-3. 새로운 노드의 parent를 추가해 준다 (가장 왼쪽의 key값)

Leaf Node Split

Leaf Node Split의 경우 처음 n/2개의 key를 기존 노드에 남기고 나머지 key값을 새로운 node에 넣는다
새로운 노드의 가장 왼쪽 key를 parent 노드로 사용한다
이때 parent 노드에도 자리가 없으면 non leaf node split이 필요하다
worst case는 모든 노드를 split하는 경우로 높이가 1 증가한다
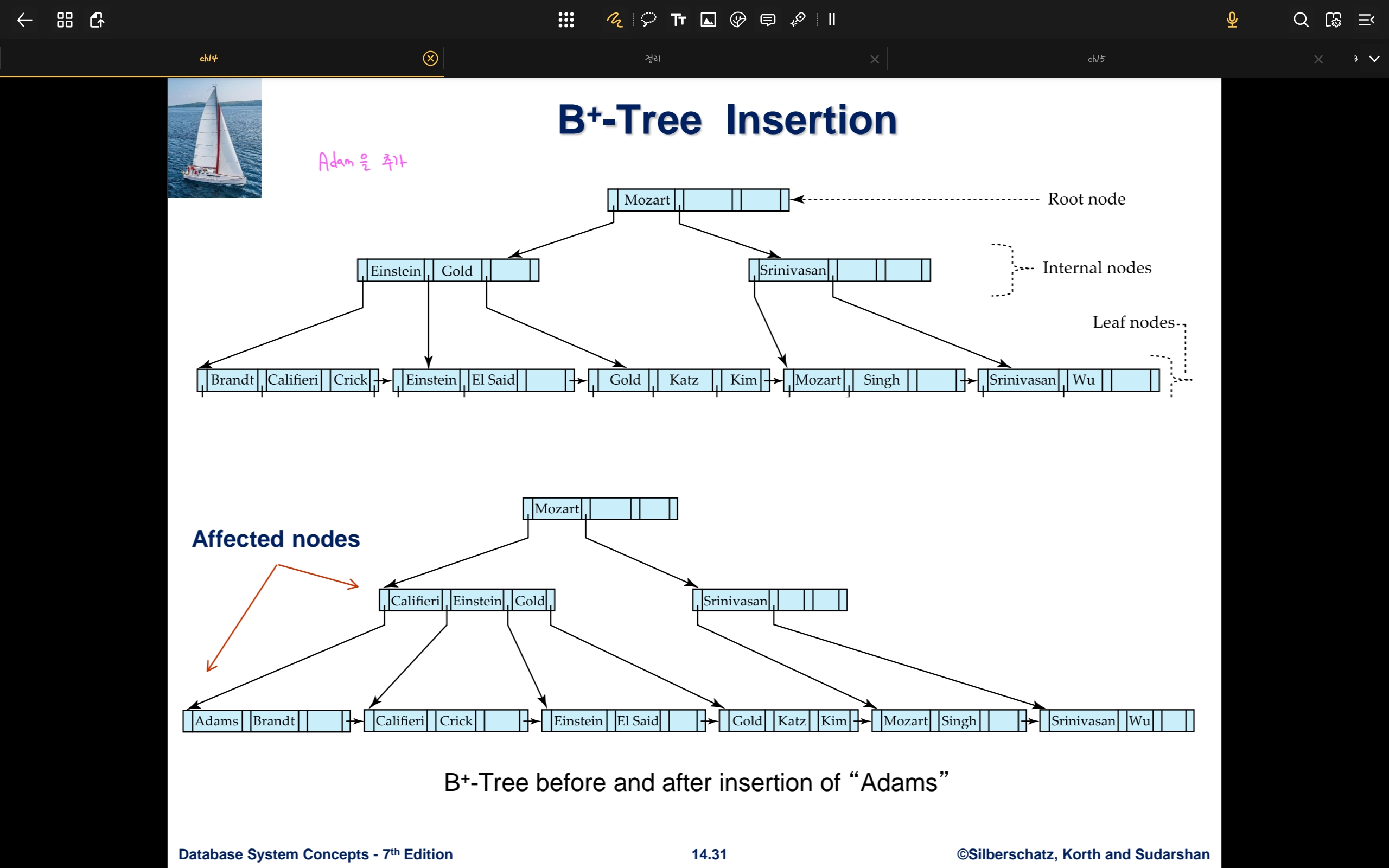
위의 B+Tree에서 Adam을 추가하는 상황

Adam이 들어갈 Leaf Node의 위치를 탐색
- 가장 왼쪽 노드에 위치해야 하는데 해당 노드에 자리가 없으므로 Leaf Node를 Split해야 한다
- Adam, Brandt, Califieri, Crick 순이므로 Califieri, Crick를 새로운 노드로 분리한다
- 새로운 노드의 가장 왼쪽 값인 Califieri를 parent 노드로 보낸다. 따라서 parent 노드는 Califieri, Einstein, Gold가 된다

Non Leaf Node Split

overflow된 노드를 저장할 임시 노드 M을 생성하여 key값을 모두 저장한다
해당 노드의 앞 절반을 기존 노드에 저장하고 뒤 절반은 새로운 노드에 저장한다
이 때 역시 새로운 노드의 가장 앞에 키가 parent노드로 사용되는데 이 경우에는 키 값을 새로운 노드에 삽입하지 않고 parent 노드에만 삽입하게 된다
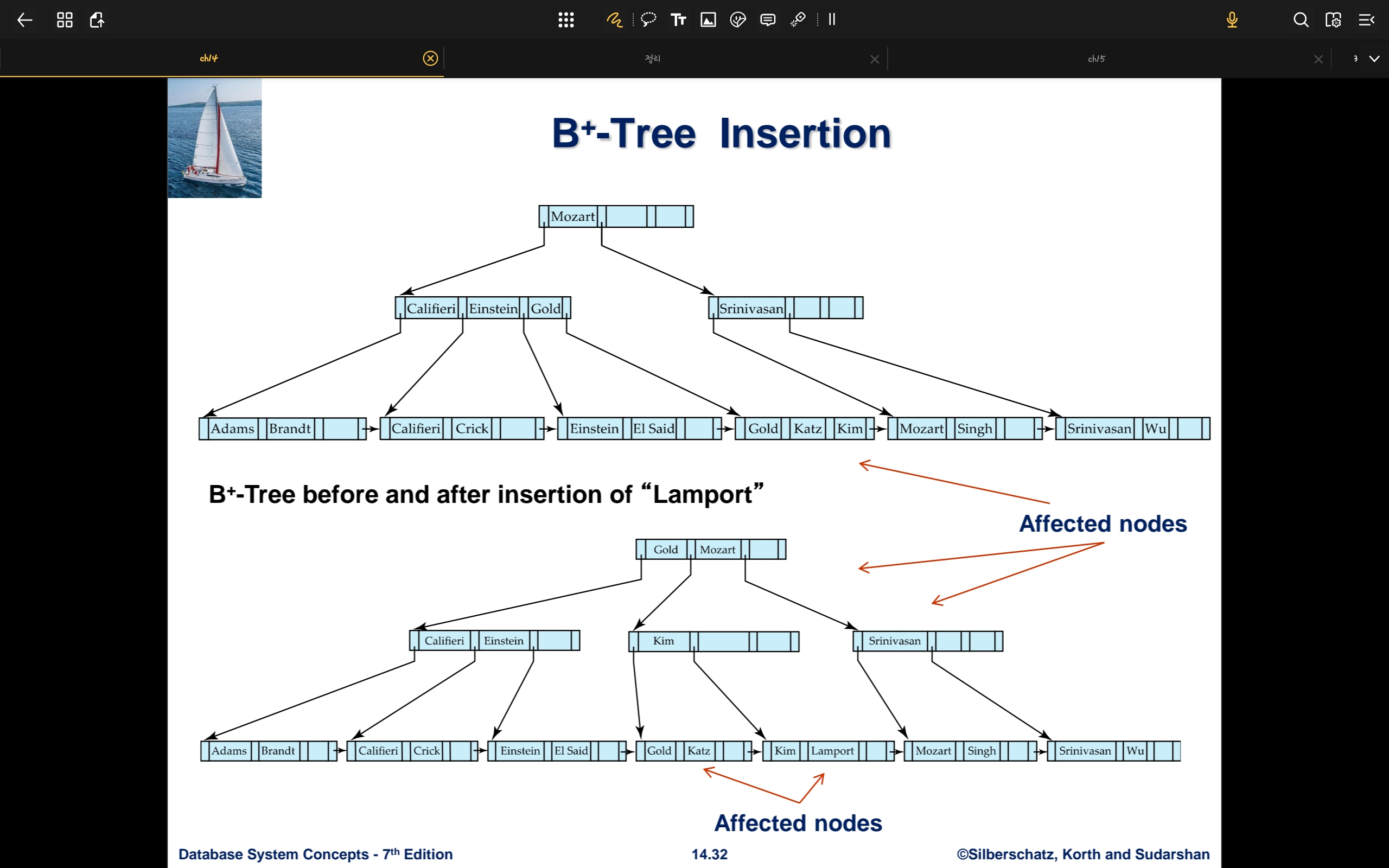
Lamport를 추가하는 상황

Lamport가 들어갈 Leaf Node의 위치를 탐색
- 왼쪽에서 4번째 노드에 들어가야하는데 overflow가 발생
- 해당 노드의 앞 절반, 뒤 절반으로 분할 뒤 새로운 노드의 가장 앞에 값인 Kim이 parent 노드로 올라간다
Kim을 parent 노드에 추가해야하는데 overflow 발생
- 기존 노드 Califieri, Einstein
- 새로운 노드 Gold, Kim
- 새로운 노드에서 Gold가 parent로 올라가고 삭제한다
- root 노드에서 Gold, Mozart가 된다

B+Tree Deletion

해당 search-key를 삭제한다 (leaf node)
underflow가 발생한다면
2-1. merge가 가능하다면 merge (항상 왼쪽 노드로 오른쪽 노드를 merge)
- 빈 노드 삭제, 빈 노드의 부모 노드의 ey 삭제
- 이 때 부모 노드가 underflow 된다면 반복
2-2. merge 불가능하다면
- Key 재분배
parent key를 update한다 (child 노드의 가장 왼쪽의 key로)
root가 child가 한개 이하이면 root를 삭제한다

leaf 노드 키 재분배

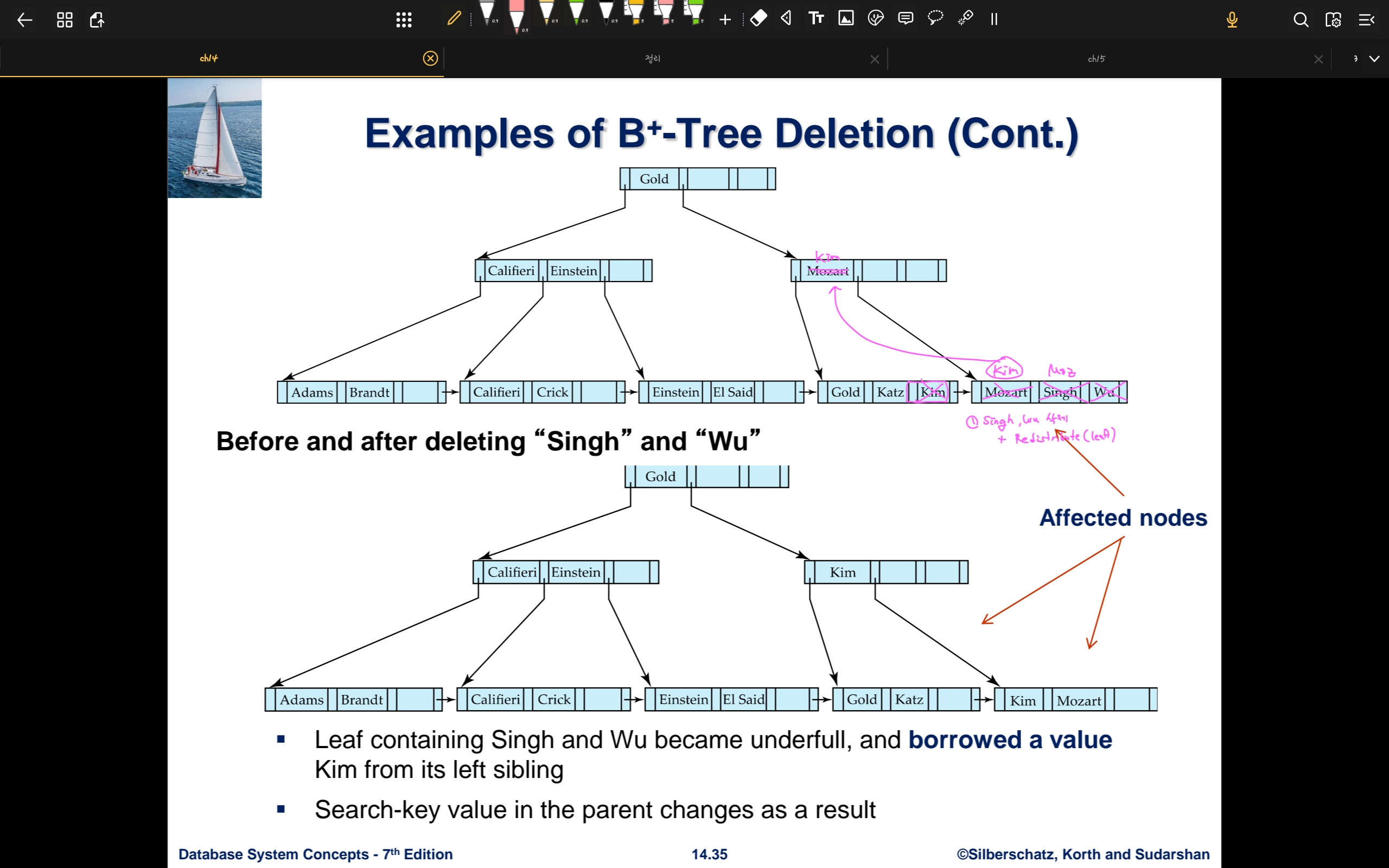
Singh, Wu를 삭제하는 경우
Wu 삭제 시점에 underflow가 발생
병합을 시도하나 실패 (항상 왼쪽 노드로 병합)
Leaf 노드에서의 키 재분배 진행
- 왼쪽 노드의 가장 오른쪽 key, pointer 를 오른쪽 노드로 넘긴다
- Parent의 key를 가장 왼쪽 key로 update한다

Non leaf 노드 키 재분배

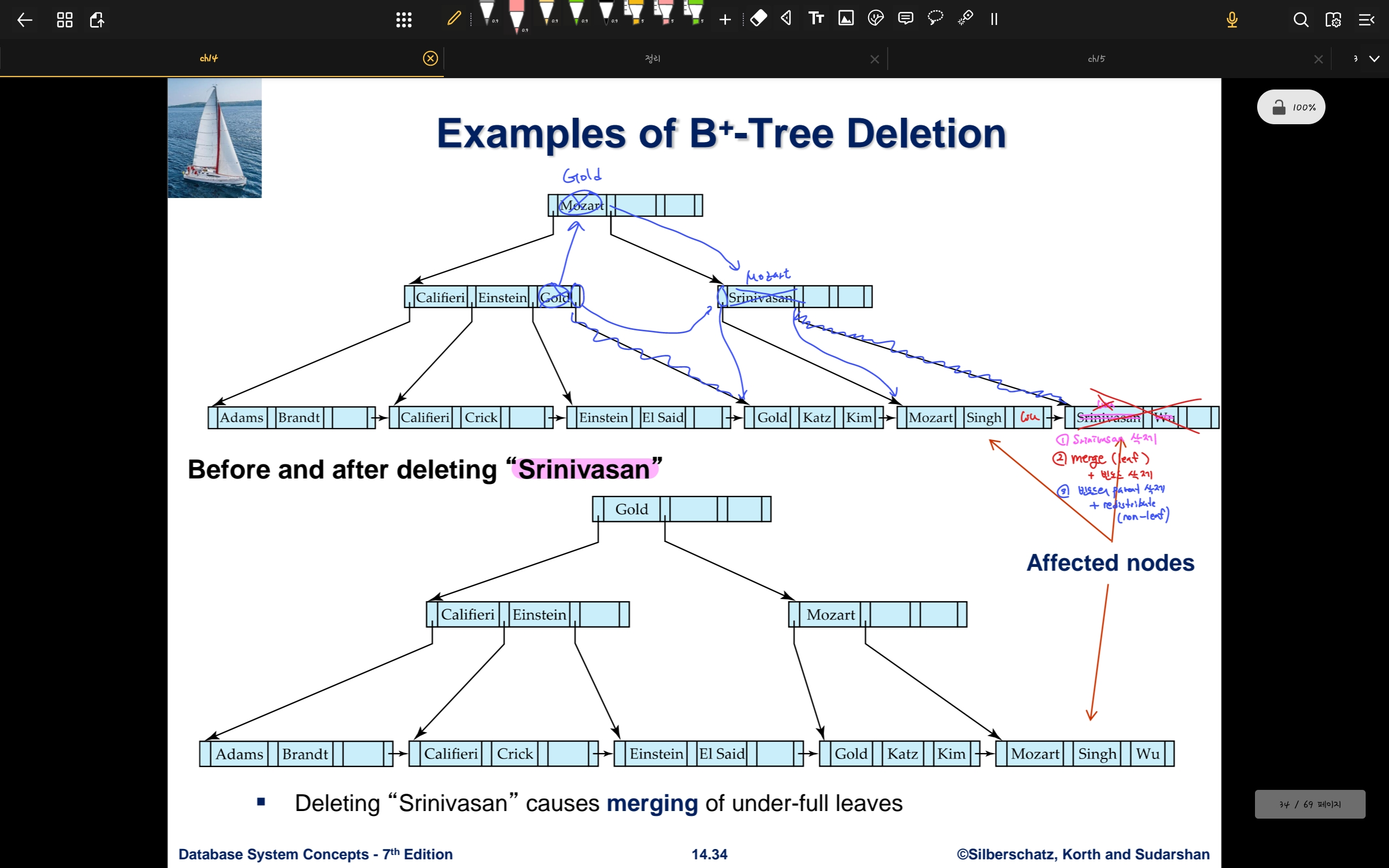
Srinivasan을 삭제하는 경우
오른쪽 노드에서 Wu를 가져와 merge
오른쪽 노드가 삭제됨으로 parent 노드의 키,포인터 삭제 -> parent 노드의 underflow
parent 노드도 merge를 시도하지만 실패 -> non leaf 노드 키 재분배
먼저 왼쪽 노드의 가장 오른쪽 key는 상위 노드로, pointer는 형제노드로 이동
그리고 기존의 상위노드의 key가 형제노드로 내려간다

root 제거

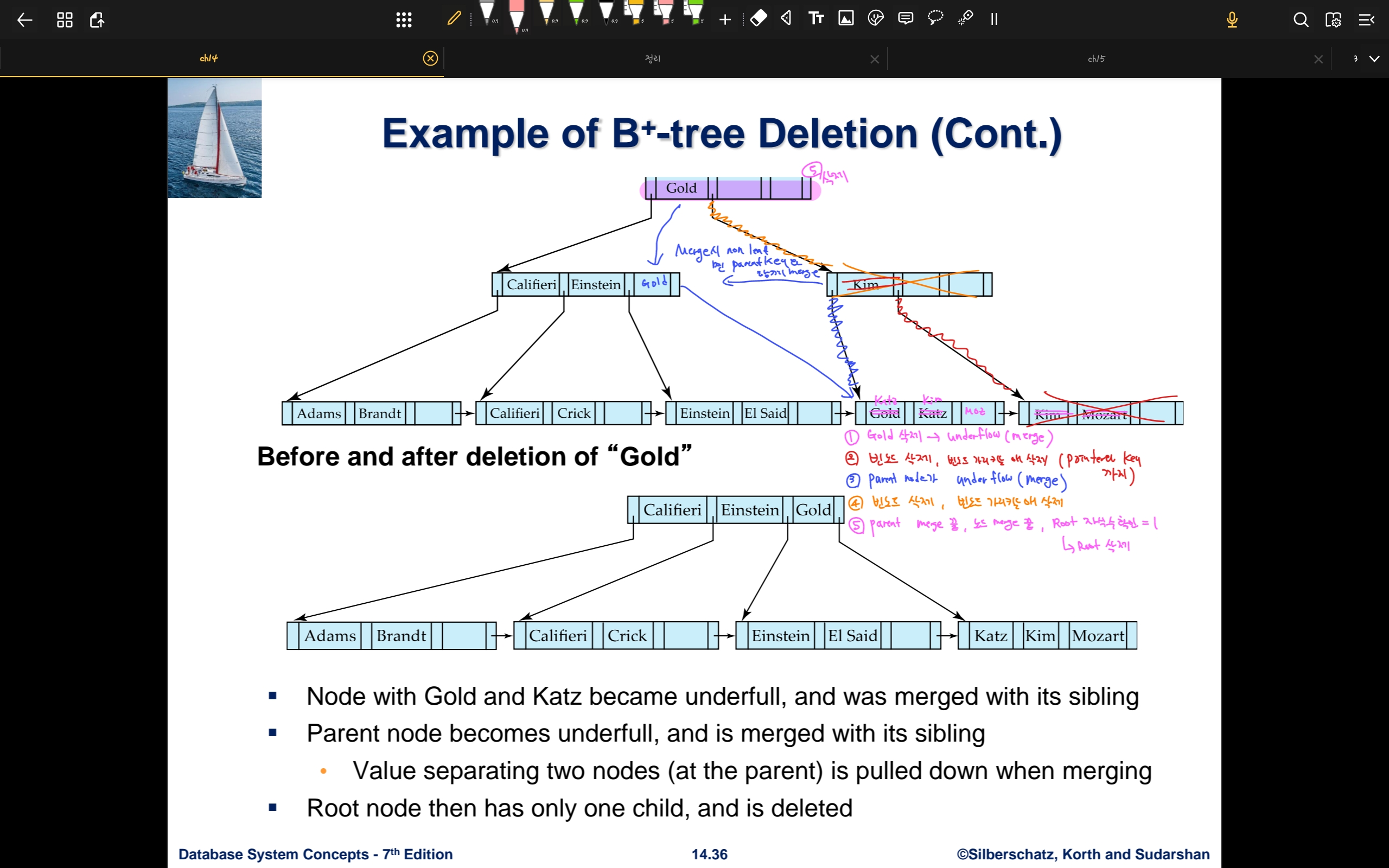
Gold를 제거하는 상황
merge를 진행하고 오른쪽 노드를 제거한다
parent 노드 또한 underflow가 발생하여 merge
parent merge를 진행할 때 non leaf의 경우 상위노드의 키 Gold와 pointer가 함께 merge된다
빈노드가 삭제되면서 parent인 Gold의 pointer, key를 삭제한다
root의 자식 수가 확인 했을 때 1이기 때문에 root를 삭제 한다

정리
leaf node merge : 왼쪽으로 합체 후 빈 노드 제거, 빈노드의 parent key,pointer 모두 제거
non leaf node merge : pointer를 왼쪽 노드로 합체, 상위노드의 key를 왼쪽 노드에 추가, 빈 노드 제거
leaf key distribution : 왼쪽 노드의 가장 오른쪽 key는 상위 노드로 보내고 key, pointer는 오른쪽 노드로 보낸다, 기존 parent key는 제거
non leaf key distribution : 왼쪽 노드의 가장 오른쪽 key는 상위 노드로, pointer는 오른쪽 노드로 보낸다, parent key는 오른쪽 노드로 이동

Cost

삽입 / 삭제의 비용의 worst case는 tree의 높이이다.
실제로 merge, split은 자주 발생하지 않기 때문에 대부분의 경우 더 빠르다고 한다
또한 internal node는 이미 버퍼에 있을 가능성이 높다

B+Tree File Organization

B+Tree의 형태로 레코드 전체를 저장하는 방식이다
B+Tree를 사용하기 때문에 동일한 장점을 가진다
하지만, 레코드 전체를 저장해야하기 때문에 노드에 들어갈 수 있는 요소의 개수가 더 작아진다
즉, B+Tree의 차수가 더 작아지고 높이가 더 높아지기 때문에 더 느려진다

B+Tree Issues

만약 레코드의 위치가 변경된다면, index의 pointer도 변경되어야 한다
만약 B+Tree File Organization을 사용하는 경우, index의 pointer가 주소 값 대신 B+Tree File Organization의 key값을 가지도록 하면 변경 할 필요가 없다
이 경우에 index를 2번 타야하기 때문에 비용이 더 커지지만
Split 비용을 줄일 수 있다

B Tree

B+Tree와 비슷한 구조 이지만 B+Tree와 다르게 internal-node 역시 search-key를 가진다
즉, 모든 노드가 search-key인 형태이다. (B+Tree는 leaf 노드만 search key)
따라서 노드 수가 더 작고, 리프 노드 도달전에 레코드를 찾을 수 있다는 장점이 있다
그러나, 다음과 같은 단점이 있다
- 대부분의 값은 노드에 존재하기 때문에 결국 leaf 노드까지 탐색하는 경우가 많다
- 노드가 다음 노드 포인터, 레코드 포인터, 키를 포함하기 때문에 크기가 더 크다 (차수가 더 낮아진다)
- insert, delete가 더 복잡하다
- 가장 큰 단점은 B+Tree 처럼 Range 쿼리 시에 쭉 할 수가 없다