출처: DSBA 연구실 유튜브 와 DSBA 연구실 강의자료 를 참고하면서 스터디를 진행하였습니다.

주제: Anomaly Detection_Isolation Forest

---

1. Motivation: Few and Different

• 소수 범주, 훨씬 적은 객체들로 구성되어 있을 것임

• normal 범주에 속하는 객체들과는 다른 속성값을 가지고 있을 것임

• 특정 객체 하나를 고립시킬 수 있는 tree를 만들 수 있다면, abnormal data는 isolation이 쉬울 것임
  📌 쉽다 = 몇 번의 split을 하지 않아도 isolation이 될 수 있다는 의미

• 반대로 normal data는 isolation이 어려울 것임
  📌 어렵다 = 생각보다 isolation이 하기 위해 split을 많이 해야 한다는 의미

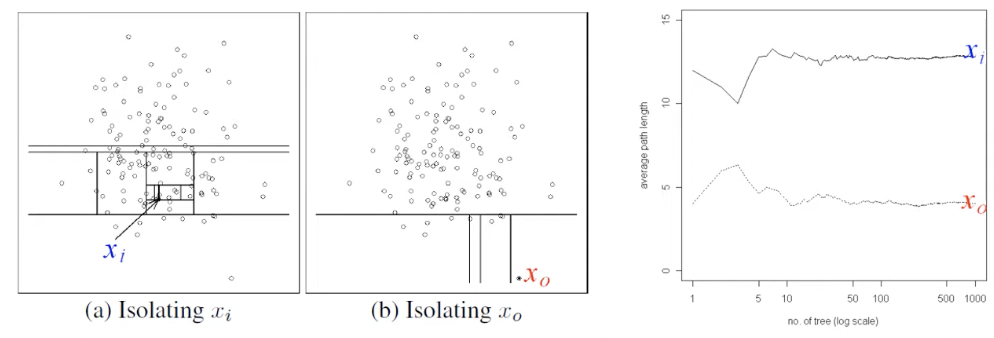
• 기존 의사결정 나무의 경우 Information gain이 크게 되는 변수와 기준점을 찾아서 기준점을 가지고 영역을 분리 함

• 고립시키는 tree 알고리즘 = "막" 함
  📌 임의의 변수를 선택하고 임의의 값을 사용함
  📌 random 변수 & random value을 가지고 isolation이 될 때까지 split 진행
  📌 한번 split 후 isolation 시키고 싶은 변수가 어느 쪽에 있는지 판단을 하고 isolation 시키고자 하는 객체가 존재하지 않는 부분을 버리게 됨

---

2. Methodology

2.1. Idea

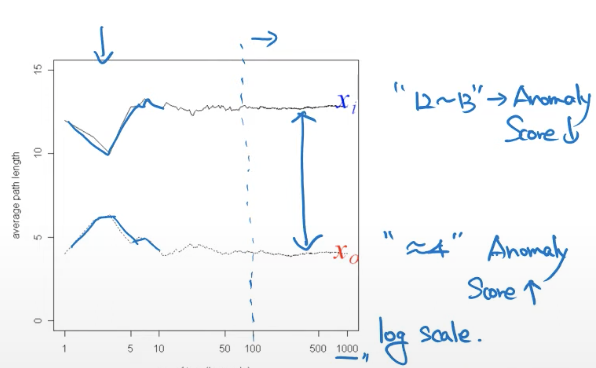
• split이 적게 되면 anomaly score을 크게 만들어주고 split을 많이 하게 되면 anomaly score을 낮게 만들어주자!

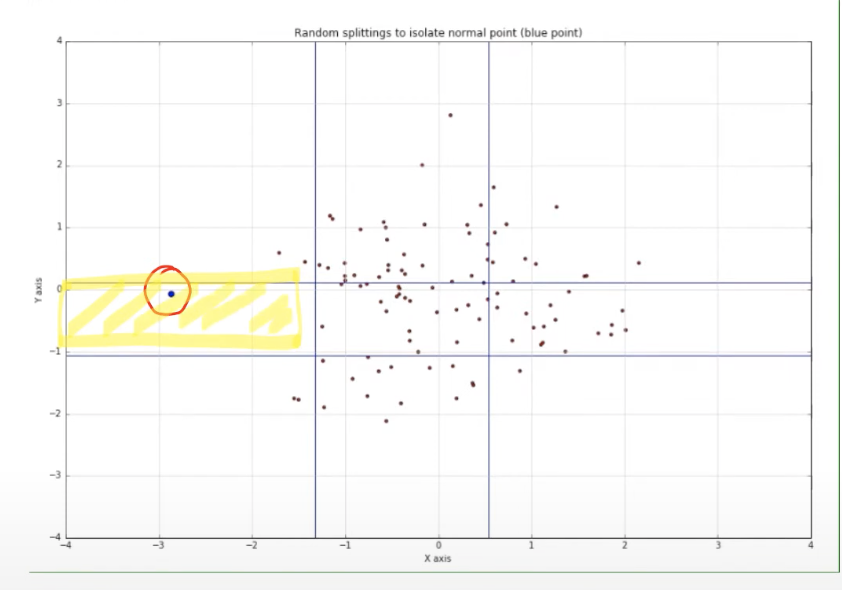
직관적으로 한번 생각해보자!

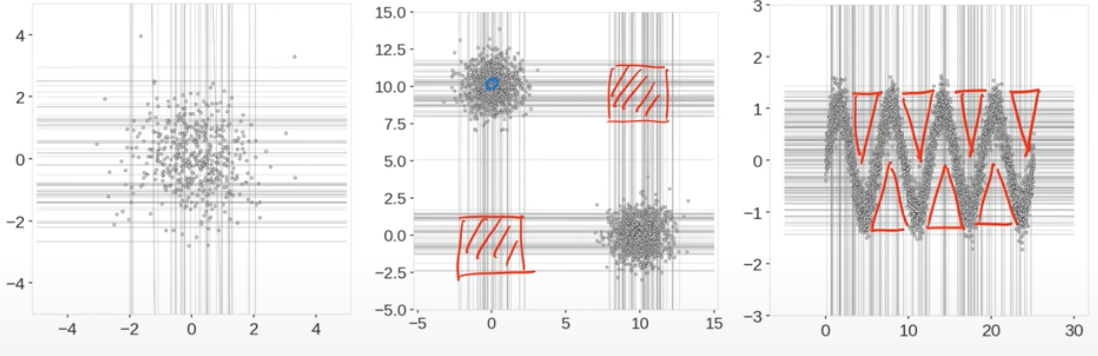
• 위의 그림의 빨간색 동그라미 안에 있는 점은 누가봐도 abnormal data인데, 이를 isolation 하기 위해서는 임의로 4번정도의 split을 거쳐야 했음.

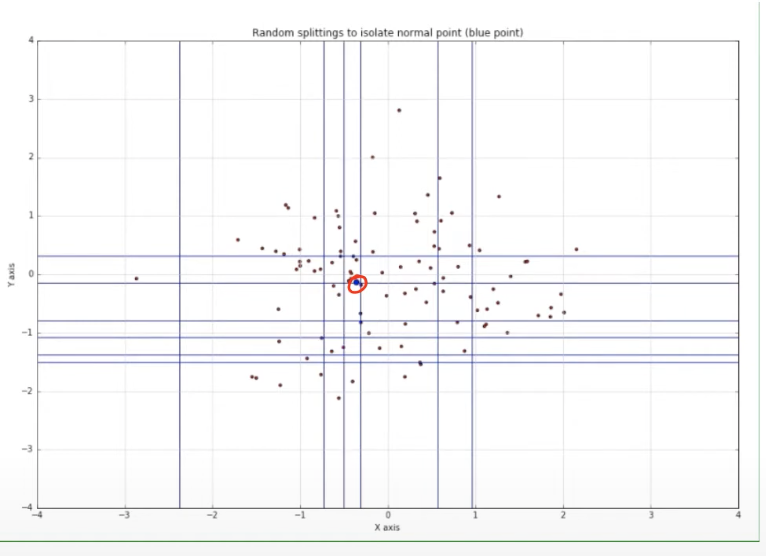
하지만!

• 위의 그림은 빨간색 동그라미 안에 있는 점은 normal data인데, isolation 하기 위해서는 약 12번정도의 split을 거쳐야 했음.

그래서 split이 적게 되면 Anomaly Score을 크게 만들어주자!

반대로 split이 많게 되면 Anomaly Score을 낮게 만들어주자!

라는 것이 Isolation Forest의 핵심 Idea임

---

2.2. Algorithm

(1) random한 변수를 선택해서 그 변수의 아무 값이나 사용을 해서 split을 하고, isolation 될 때까지 반복함.

(2) 충분히 많은 횟수를 덮어씌우게 되면, random의 random하게 되면 "경향성"이 나타날 수 있고 이를 통해 Anomaly Score을 산출할 수 있음.

---

2.2.1. Pseudo Code

---

2.3. Characteristics

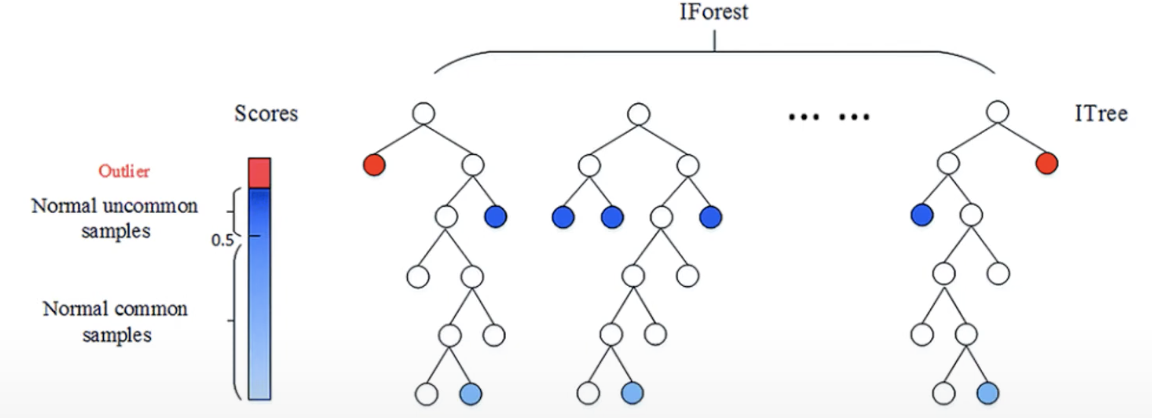
• Isolation이 얼마나 수월한가 어려운가를 가지고 이상치 score을 설계할 수 있음.

• Isolation Tree를 만들어서 해당하는 Tree를 충분히 많이 만들게 되면 이들이 가지고 있는 score의 집합체는 충분히 일반화된 성능과 높은 판별력을 가질 수 있음.

• 위의 그림을 확인해보면, 빨간색 노드일수록 이상치일 가능성이 높을 것이고 하늘색 노드일수록 이상치가 아닐 가능성이 높을 것임.

---

3. Definition

: sample data X가 주어졌을 때, atttribute q와 split value p를 랜덤하게 선택해서 재귀적으로 영역을 분할을 함.

📌 $|X|$ = $I$ = $Isolation$

아래 두 경우는 알고리즘의 효율성을 위해 사용됨

• The tree reaches a height limit

• All istances in X have the same value

Path Length

• x가 루트 노트로부터 터미널 노드까지 가는 데 걸리는 edge의 수를 의미함

• 즉, 몇 번 split 해서 갔는지?

split된 횟수는 평균적으로 어떻게 normalize 될 수 있을까?

Euler's constant (오일러 상수)

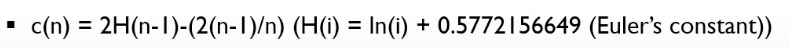
Novelty Score

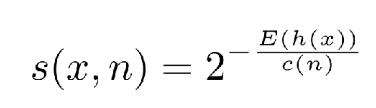
• $c(n)$: 평균 path length

• $E(h(x))$: 1개의 tree에 대해 x를 isolation 시키기 위한 path length

-- $E(h(x))$ -> $c(n)$, $s$ -> 0.5, 2^-1
-- $E(h(x))$ -> 0, $s$ -> 1, $2^0$
-- $E(h(x))$ -> $n-1$, $s$ -> 0, 0

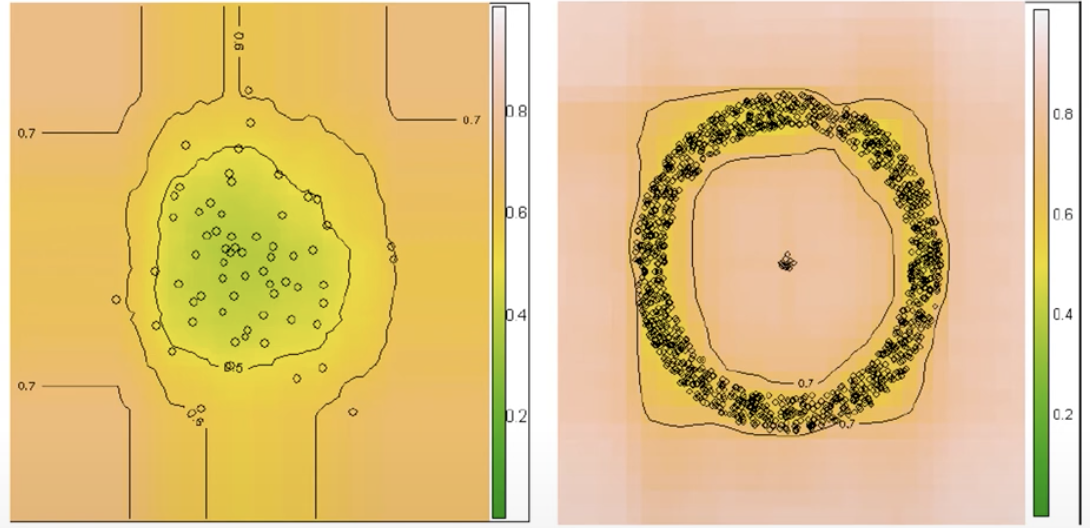
• 위의 등고선 그림을 확인해보면, 오른쪽 그림은 원형에 정상적인 데이터와 가운데에 비정상적인 데이터를 볼 수 있음

---

4. Empirical Evaluation

• Datasets
  

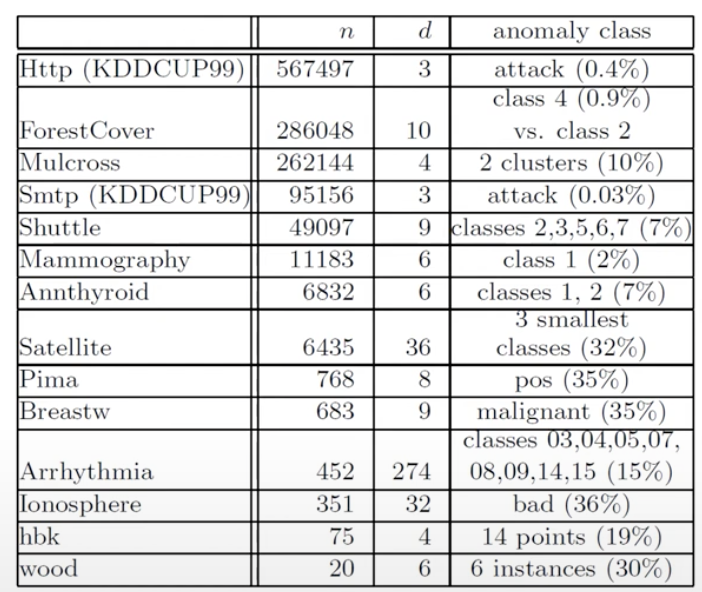
• Performance (in terms of AUROC)
  

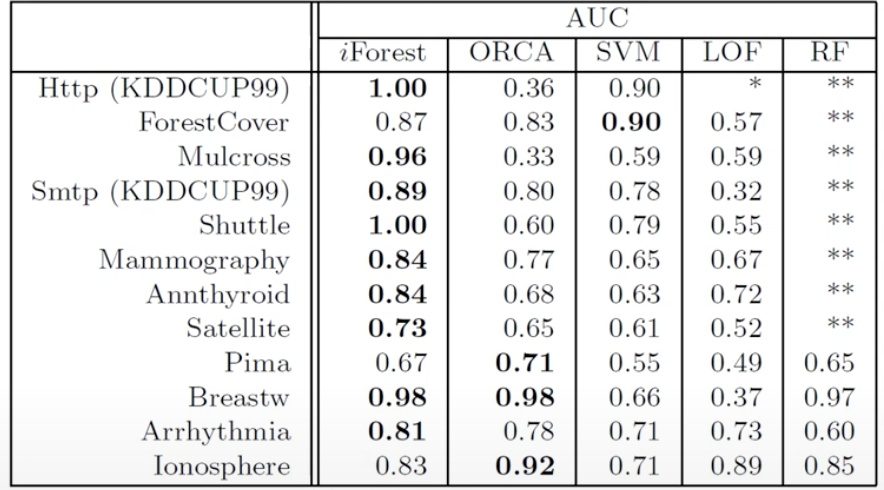
📌 Isolation Forest가 높은 탐지 성능을 보임

• Performance (in terms of computational complexity)
  

---

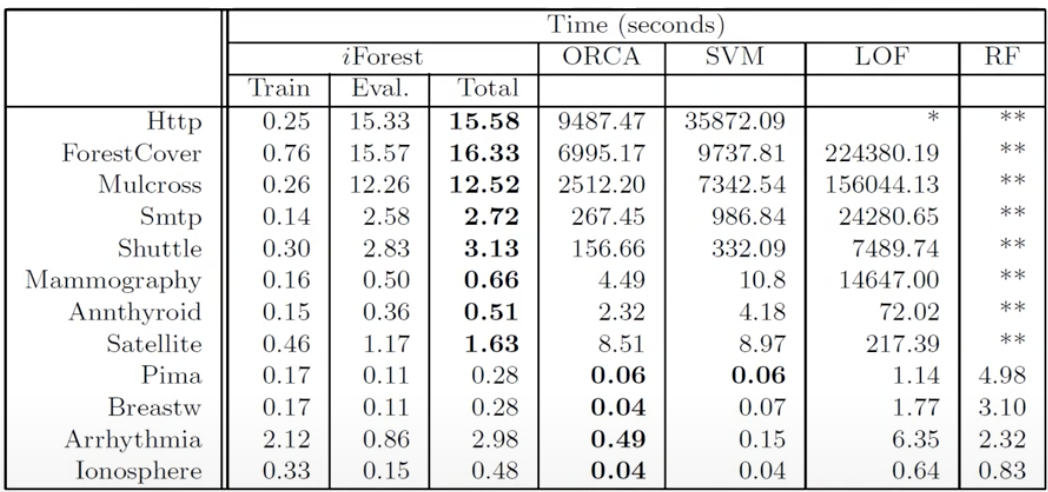
5. Extended Isolation Forests

5.1. Motivation

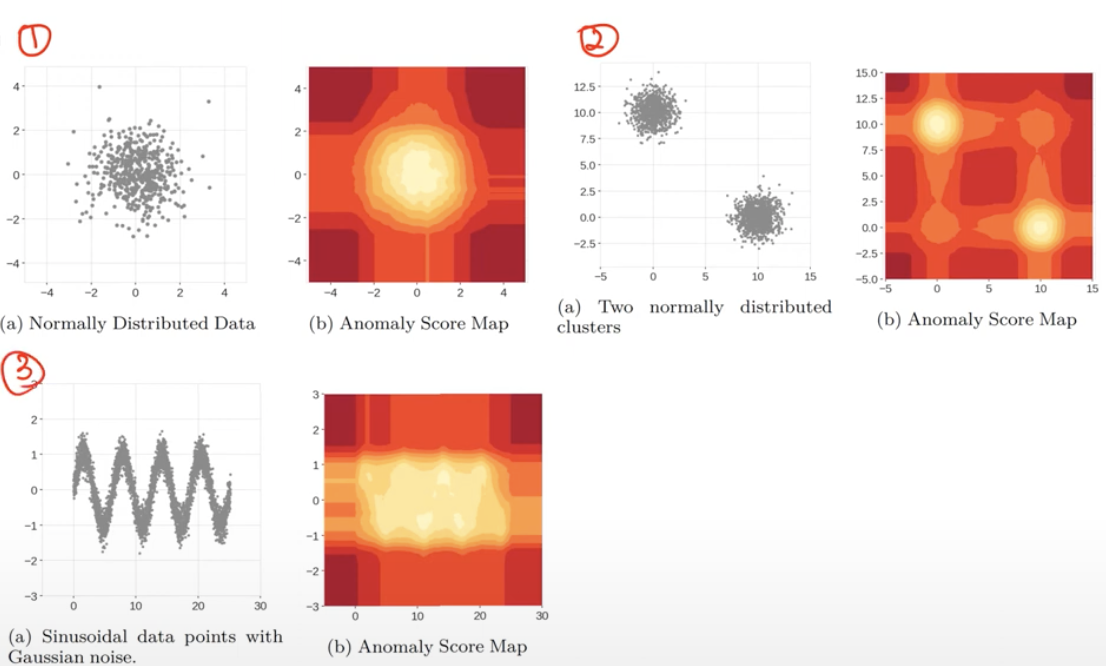
• Isolation Forests의 개념을 확장 시킨 Extended Isolation Forests 등장

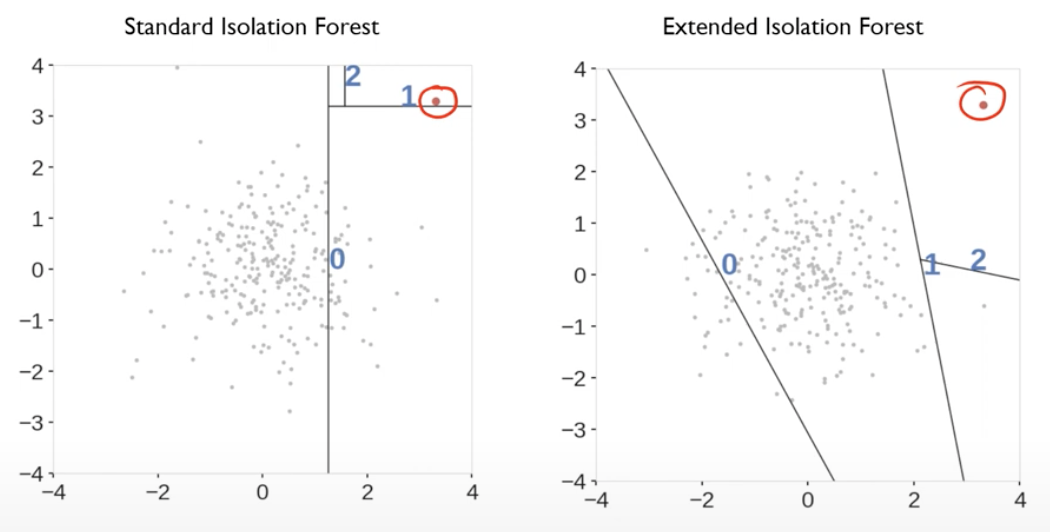
• 1번 부분은 잘 작동됨.

• 2번, 3번은 실제로는 이상치일 가능성이 높은데, Isolation Forest에서는 정상 가능성이 높음.

---

5.2. Contribution

• a branch cut that has a random "slope"

• 축에 수직이 아니라, 기울기가 있는 선으로 구분하는 것을 허용하는 것이 핵심임

---

5.3. Illustrative Example

---

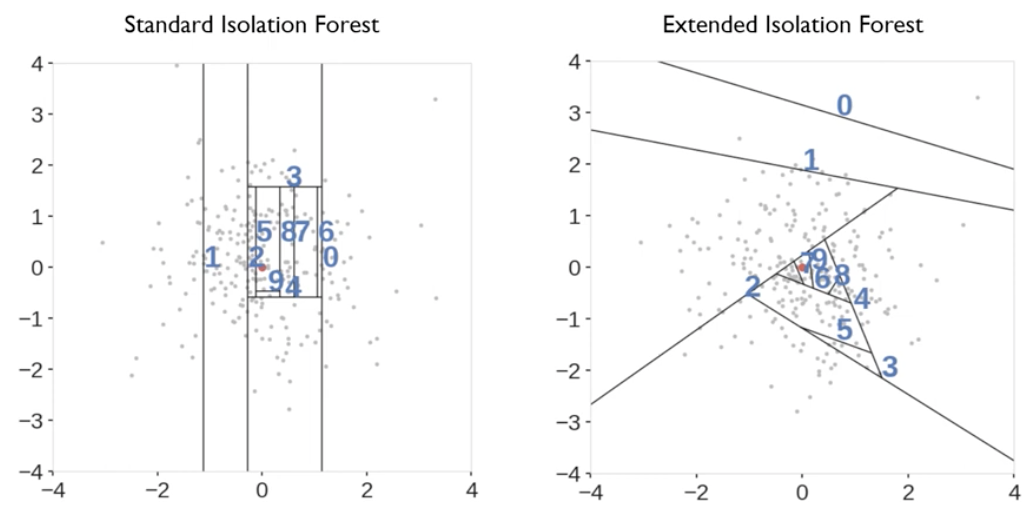
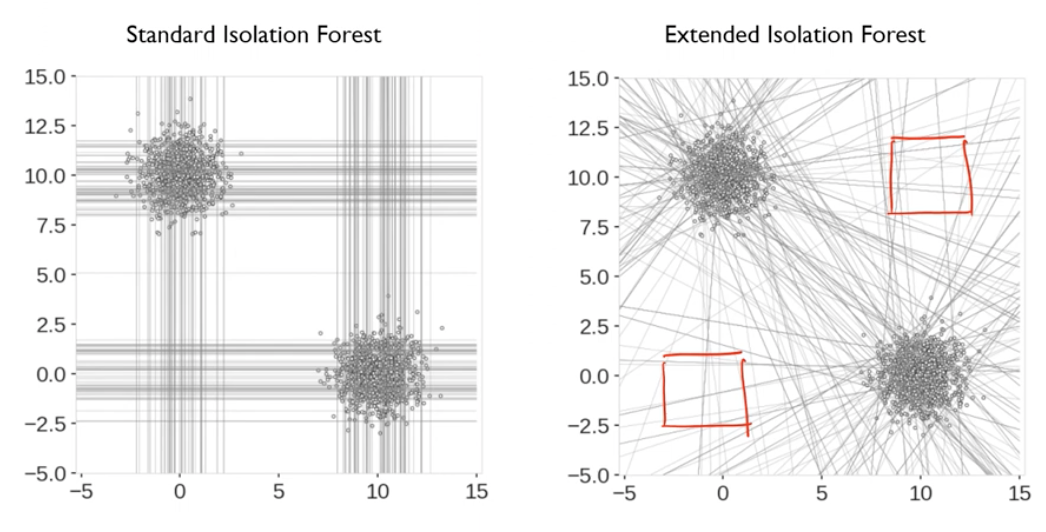
5.4. Pseudo Code

• 기울기와 y절편을 임의로 정해줌으로 인해서 split의 자유도를 높여줌

---

5.5. Anomaly score distribution

---

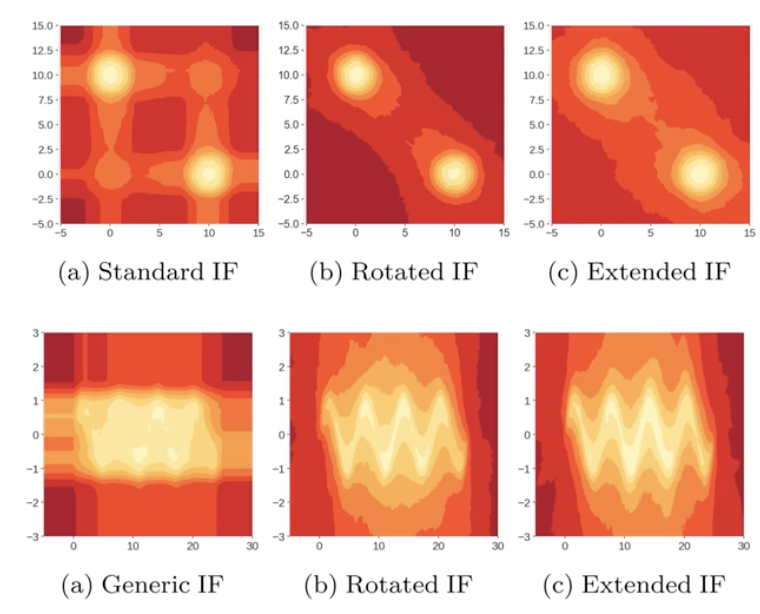
🎯 Summary

• Extended Isolation Forests에서 경이로웠음.

• 현존하는 알고리즘 중에 풀지 못하는 case를 하나의 그림, 시나리오, 결과물 위주로 비교하는 것이 중요한 방법론이라고 생각이 듬.

• 또한 논문 주제 search를 할 때 다양한 SoTA 모델을 뜯어보고 SoTA 모델이 특정 상황에서 작동하지 못한다면, 이것을 연구해보면 좋을 것 같다는 생각도 듬. 그러면 리뷰어들에게 설득하기 쉬울 거 같음.

• IF와 EIF 둘다 간단한 방법론이었지만 속도가 빠르고 설명 가능한 방법론이었음. 이 방법론을 좀 더 공부해봐야겠음!!

• 강의자료와 유튜브를 무료로 볼 수 있게 한 DSBA 연구실에 감사의 인사를 전합니다.

📚 References

• Youtube

• https://youtu.be/puVdwi5PjVA?si=z8ThHyaHUaqIpnGi, DSBA 연구실 유튜브

• 강의 자료

• https://github.com/pilsung-kang/Business-Analytics-IME654-/blob/master/03%20Anomaly%20Detection/03-7_Anomaly%20Detection_Isolation%20Forest.pdf, 강필성 교수님 github