단일 연결리스트와 이중 연결리스트
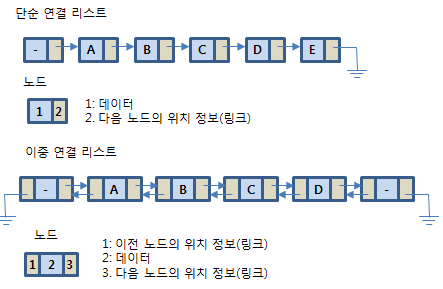
단일 연결리스트는 이전노드의 위치정보가 없지만,
이중 연결리스트는 이전노드의 위치정보가 있다.
때문에 단일 연결리스트의 삭제 시간복잡도는 O(n)이 되지만,
이중 연결리스트의 삭제 시간 복잡도는 O(1)이 된다.
연결리스트의 실제사례
연결리스트와 배열의 차이
연결리스트 (추가/삭제에 용이)
- 메모리 상에 원소들이 연속적으로 위치하지 않는다.
- 데이터 추가 삭제가 용이.
- 메모리 효율적 사용 가능. 링크로 이루어져 있어서 메모리가 동적으로 할당되기 때문.
- 테이터 검색할 때 별로임.
배열 (탐색/정렬에 용이)
- 메모리를 연속적으로 할당
- 탐색에 능함
- 중간에서 원소 넣고 빼기 얼려움
해싱이란 무엇인가?
해싱은 가변 크기의 입력값에서 고정된 크기의 출력값을 생성해내는 과정을 의미합니다.
해시 충돌 해결법
1) 체이닝: 버켓 내에 연결리스트를 할당하여, 버켓에 데이터를 삽입하다가 해시 충돌이 일어나면 연결 리스트로 데이터들을 연결
2) 오픈 어드레싱: 다른 빈 버켓에 데이터 삽입
2-1) 선형탐색: 다음, 혹은 몇 개 건너뛴 곳에 데이터 삽입
2-2) 제곱탐색: 제곱만큼 건너뛴 버켓에 데이터 삽입
2-3) 이중해시: 해시충돌시 다른 해시 함수를 적용
-
체이닝의 장점: 단순하다
-
체이닝의 단점: 해시테이블이 채워질수록 Lookup 성능저하가 Linear하게 발생한다. (원래 hashTable의 탐색 시간복잡도는 O(1)인데, 버켓 내의 연결리스트가 길어지면 결국 시간복잡도가 O(n)에 가까워지면서 해시테이블의 장점이 무색해짐)
-
오픈어드레싱 장점: 추가적인 저장공간이 필요없으며, 삽입이나 삭제 시 오버헤드가 적다. 근데 걍 계산이 복잡해짐...😖
해시함수의 특징
- 어떤 입력 값에도 항상 고정된 길이의 해시 값을 출력한다.
- 입력 값의 아주 일부만 변경되어도 전혀 다른 결과 값을 출력한다.(눈사태 효과)
- 출력된 결과 값을 토대로 입력 값을 유추할 수 없다.
- 입력 값은 항상 동일한 해시 값을 출력한다.
해시테이블 용어정리
1) storage: 해시테이블에서 자료를 저장하는 전체 공간
2) bucket: 각 해시테이블에 인덱스 별로 존재하는 슬롯
3) tuple: 해시 충돌시 버켓 내부에 자료들을 연결시켜 저장할ㄹ 때, 이 자료들이 저장되는 버킷의 내부 공간.
튜플과 배열의 차이: 튜플 내의 값은 수정 안됨. 추가, 삭제도 안 됨. 다른 것으로 재할당은 됨. 문자열과 유사.
비트연산자
컴퓨터에서 정보표현의 최소 단위인 '비트'.
- &: 양 쪽을 이진수로 바꾼 후 각 자리를 &연산
- |: 양 쪽을 이진수로 바꾼 후 각 자리를 |연산
- ~: 자리 수의 1과 0 반전 (참고사항: 32비트 운영체제에서는 전체 서른두 개의 비트 중 맨 상위가 부호비트임. 0양수 1음수. 1111 1101 = -3)
- <<: 왼쪽 수를 오른쪽 수 만큼 왼쪽으로 비트이동
예) 4 << 2 (4를 2비트 왼쪽으로 이동)
0000 0100 4
0000 1000 8 (1회 이동)
0001 0000 16 (2회 이동)
결론 - "4에 2를 두번 곱해라" 4 2 2
a << b: a를 2의 b제곱만큼 곱해라 >>: 왼쪽 수를 오른쪽 수 만큼 오른쪽으로 비트이동
예) 4 >> 2 (4를 2비트 오른쪽으로 이동)
0000 0100 // 4
0000 0010 // 2 (1회 이동)
0000 0001 // 1 (2회 이동)
결론 - "4를 2로 두 번 나눠라" 4 / 2 / 2
a >> b: a를 2의 b제곱만큼 나누어라
할당연산자
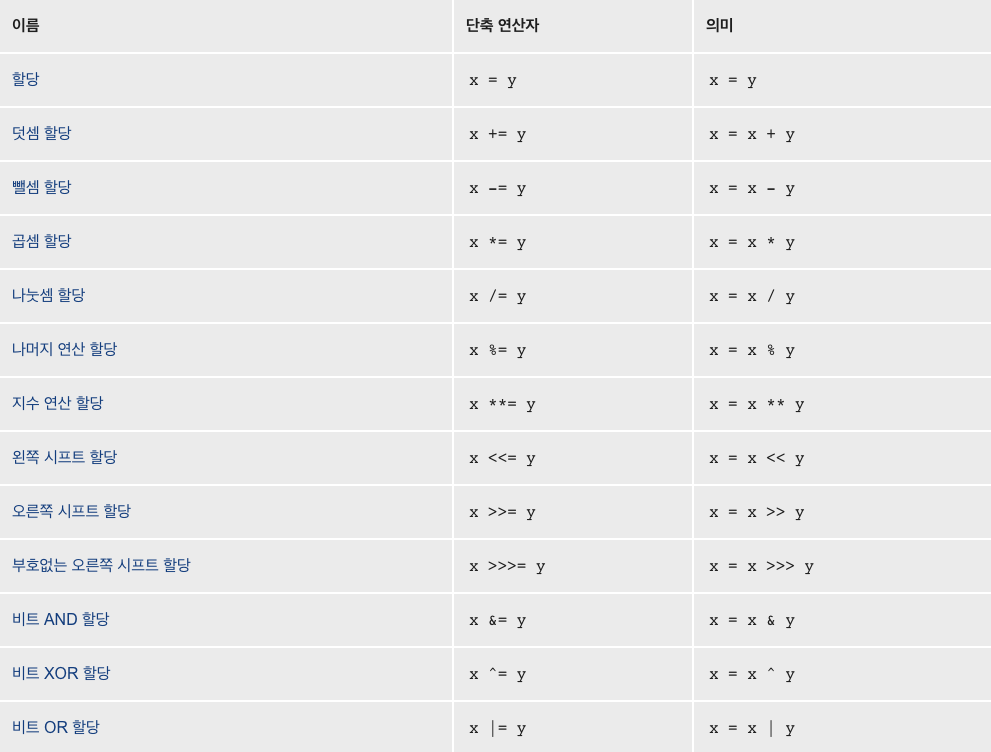
출처: MDN
