[3-2] CH7 L2 Control

Error Control

Error detection, Positive ACK, Negative ACK, Time Out

Error Detection

CRC를 확인해보고 Bit error 정도를 확인 할 수 있다. Error correction이 가능한 경우도 있다.

Automatic Repeat Request(ARQ)

1. Stop and Wait

Frame을 하나 받으면 그거에 대한 ACK이 올 때까지 기다렸다가 다음 frame을 전송하는 방식

2. Go-Back-N

수신측에서 에러난 frame이후에 받은 frame들은 다 버린다.
-> 송신측은 오류난 frame 이후에 보낸 frame도 다 다시 보내야 한다.

Ex) 1, 2, 3 frame을 받았지만 1번 frame이 깨졌다면 뒤에 온 2, 3번 frame을 저장하지 않고 버린다.
-> 송신측은 2, 3번 frame은 깨지지 않았지만 1, 2, 3번 모두 다시 보내야 한다.

3. Selective Reject

Go-Back-N에서 에러난 frame이후에 온 frame을 모두 버렸다면, 이 방식은 buffer에 저장해 둔다.
-> 송신측은 에러난 frame만 다시 보내면 된다.
하지만 구현이 어렵고, 불편해서 propagation delay가 긴 위성 전화 같은 서비스 정도에만 이용된다.

Window Size 결정

ACK이 모두 사라진 극단적인 경우를 고려해보면 다음과 같은 결과가 나온다.

sequence number가 2bit, 즉 k=2를 가정하면:

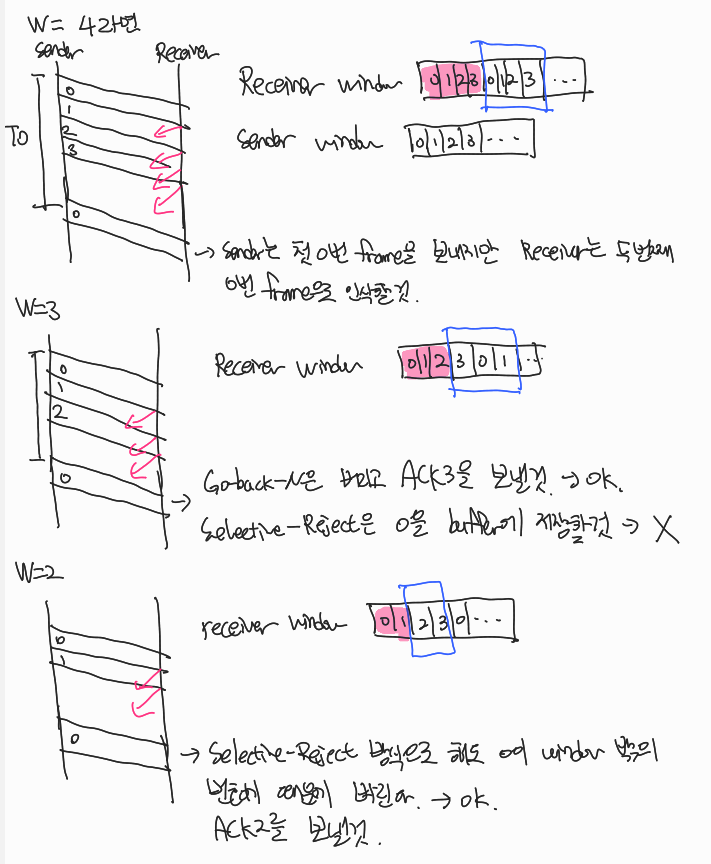
Go-Back-N

$W \leq 2^k-1$

Selective Reject

$W \leq 2^{k-1}$

Utilization; Efficiency

$U = \frac{한 frame 발송 소요시간}{한 frame 전송 완료 소요 시간}=\frac{T_f}{T_t}$

1. SAW

$\frac{ t_{frame} }{t_{frame}+2t_{prop}} = \frac{1}{1+2a}$

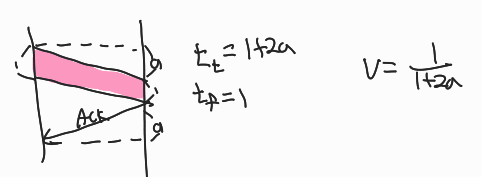
2. Sliding Window(둘 다)

$W<1+2a \rightarrow U=\frac{W}{1+2a}$

$W>1+2a \rightarrow U=\frac{1+2a}{1+2a}=1$

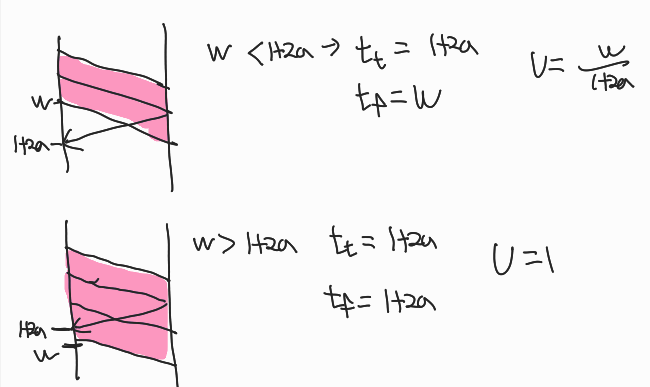
에러를 포함해서 계산해보자

$U = \frac{T_f}{T_t}=\frac{T_f}{N_r\times T_f}$ , $N_r$: 재전송 횟수 (에러가 안나면 1)

1. SAW

error rate를 p라 하면
$E(N_r)=(1-p)+p(1-p)\times2+p^2(1-p)\times3+ ...$

$=\sum_{i=1}^{\infin}i(1-p)p^{i-1}=\frac{1}{1-p}$

따라서 에러 없을 때 식에 대입해 주면
$U=\frac{1-p}{1+2a}$

이제 Sliding window방식인 두개를 보자
$N_r$값은 동일하게 $\frac{1}{1-p}$이다.

2. Selective Reject

$W<1+2a \rightarrow U=\frac{W(1-p)}{1+2a}$

$W>1+2a\rightarrow U=1-p$

3. Go-Back-N

$f(i)$를 i번 재전송할 때 다시 같이 보내야하는 frame 수 라고 해보자.
k를 매 재 전송마다 같이 보내야하는 frame 수라고 하면

$f(i)=1+(i-1)k$이 된다.

1번 재전송 해서 통과하면 끝이고, 2번 재전송 해야하면, 처음 재전송할 때, 에러난 frame과 그 이후에 보냈던 frame k개를 보내고, 두번째 재전송 때는 1번만 세어 주면 되기 때문에 이 식이 나왔다고 보면 된다.

$N(r)=\sum_{i=1}^{\infin}f(i)p^{i-1}(1-p)=\frac{1-p+kp}{1-p}$

$W<1+2a\rightarrow k\simeq W, U=\frac{w(1-p)}{(1+2a)(1-p+Wp)}$
Window 에 들어있는 모든 frame을 다 보내기 전 못받았다는 ACK을 받기 때문에 k는 1+2a와 비슷할 것이다.

$W>1+2a\rightarrow k\simeq 1+2a, U=\frac{1-p}{1+2ap}$
Window 에 들어있는 모든 frame을 다 보내고 나서야 못받았다는 ACK을 받기 때문에 k는 W와 비슷할 것이다.