What is Recursion?

📍 프롤로그

어떤 문제를 재귀적으로 풀어내는 것. 그게 나에게는 너무 어렵다.
계속 Iterative 하게 생각하게 된다. Recursive 하게 생각하는 방법으로 바꿔보자.

📍 재귀란 무엇일까?

함수가 자기 자신을 직접적으로(Directly) 또는 간접적(Indirectly)으로 호출할 때 우리는 재귀(Recursion)라고 한다. 그리고 그 함수를 재귀 함수(Recursive Function)라 부른다.

# An example of direct recursion
def directRecFun():
	# some code...
    directRecFun()
	# some code...

# An example of indirect recursion
def indirectRecFun1():
	# some code...
    indirectRecFun2()
	# some code...

def indirectRecFun2():
	# some code...
    indirectRecFun1()
	# some code...

📍 언제 재귀(Reclusion)을 사용할까?

"N번째 ... 를 계산하라", "첫 N를 나열하는 코드를 작성하라", "모든 ...를 나열하라" 등의 문제들은 재귀적으로 풀수 있는 경우가 많다. 그리고 가장 전통적인 문제로 하노이탑 문제가 있으며, 삼성 알고리즘 테스트에 단골로 출제되는 깊이우선 탐색(Depth-First Search) 문제들도 재귀적인 방법을 사용해서 푼다.

📍 재귀는 어떻게 구현할까?

재귀를 구현하기 위한 가장 보편적인 방법은 아래의 단계를 따르는 것이다.

• Step1: 종료 조건을 정의한다.
• Step2: 재귀적으로 호출하는 함수를 정의한다.(문제를 더 작은 하위문제로 나눈다.)
• Step3: 재귀가 종료되는지 확인한다.
• Step4: 하위 문제의 솔루션을 결합하여 문제를 해결한다.

이중 중요한 단계를 뽑자면 Step1 과 Step2라고 할 수 있는데,
종료조건(Step1)이 적절하지 않으면 무한루프에 빠게되고, 문제를 하위문제(Step2)로 나눌수 없으면 재귀가 성립하지 않는다. 그래서 구현할 때는 Step1 과 Step2 단계에 집중해야 한다.

📍 재귀 호출에서 메모리는 어떻게 할당될까?

모든 함수가 호출되면, 함수 정보(Local variable, return address, function pointer)가 스택에 저장되는데 이는 재귀 함수에서도 동일하게 적용된다. 스택의 특성에 따라 먼저 호출된 함수는 스택 아래, 나중에 호출된 함수는 스택 위에 위치한다. Base Case(종료조건) 에 이르면 return value를 Caller(호출한 함수)에게 전달하고 메모리는 해제된다.

예를 통해서 재귀함수가 어떻게 동작하는지 살펴보면,

def printFun(n):
    
    if(n < 1):
        return n
    else:
        print(n, end=" ")
        printFun(n-1)
        print(n, end=" ")
        return


n=3
printFun(3)

output

3 2 1 1 2 3

'

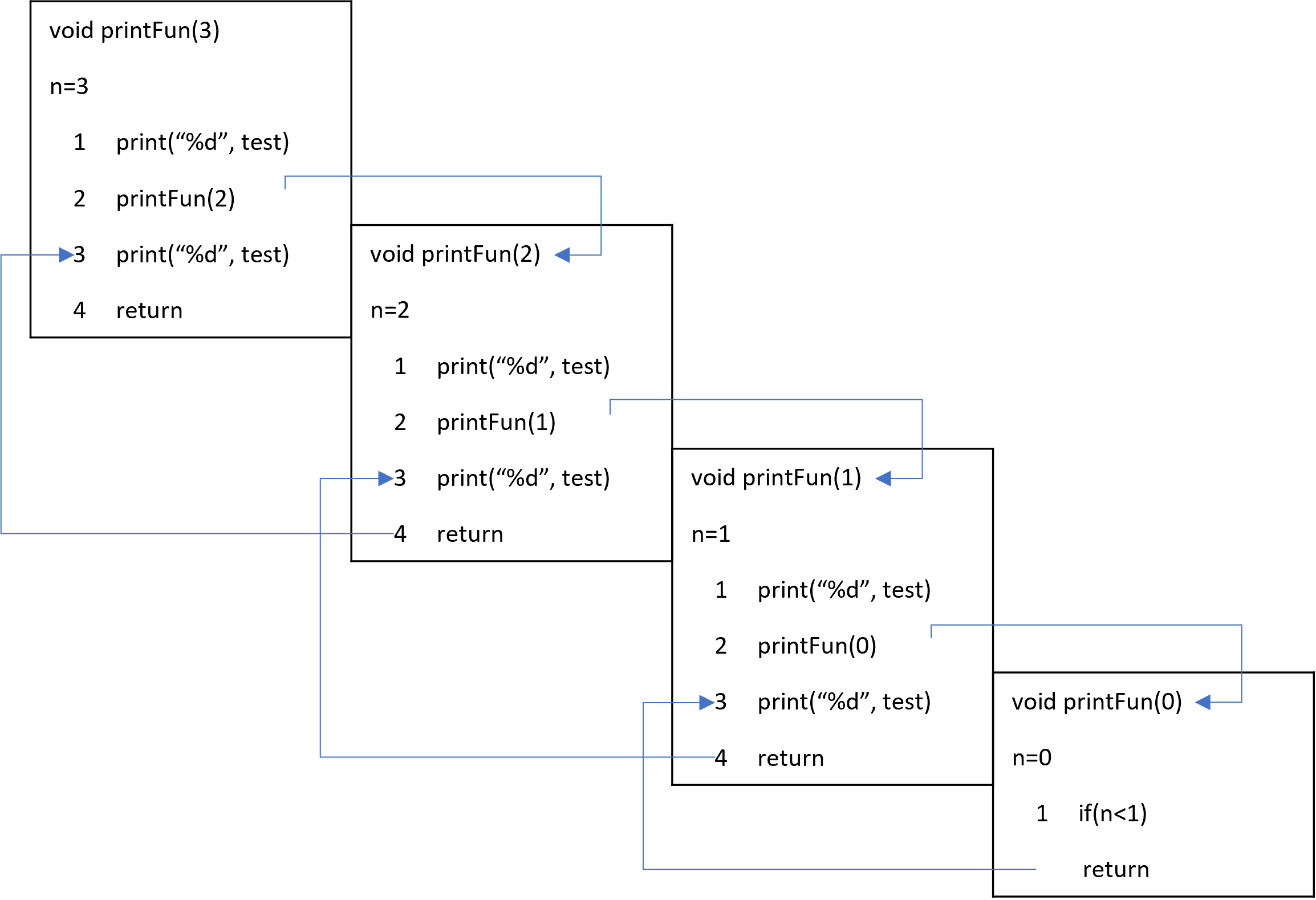
1. printFunc(3) 이 main()에 의해서 불려진다.
   n=3으로 초기화되고, 실행해야 할 구분이 다이어그램에서 보이는 것 처럼 Stack에 Push 된다.
2. printFunc(3)은 첫번째 구문을 실행하여 3을 출력 하고, printFunc(2)를 호출한다.
3. printFunc(2)는
   n=2으로 초기화되고, Statement 1부터 4를 Stack에 Push 한다.
4. printFunc(2)은 2를 출력하고, printFunc(1)를 호출한다.
5. printFunc(1)는
   n=1으로 초기화되고, Statement 1부터 4를 Stack에 Push 한다.
6. printFunc(1)은 1을 출력하고, printFunc(0)를 호출한다.
7. printFunc(0)은 if 문을지나 printFunc(1)로 리턴된다.
8. printFunc(1) 은 3번째 Statement 인 Print(n) 구문을 실행하고 printFunc(2)로 리턴된다.
9. printFunc(2)도 마찬가지로 Print(n) 구문을 실행하여 2를 출력하고 printFunc(3)으로 리턴된다.
10. printFunc(3)에서 Print(n) 구문을 실행하여 3을 출력하면 모든 함수가 종료된다.

이제 왜 함수의 실행 결과가 3 2 1 3 2 1 이 아니라 3 2 1 1 2 3 이렇게 출력되는지 이해할 수 있다. 이는 재귀적 호출이 Stack의 특성 사용하기 때문이다.

재귀를 이해하기 위해서는 Stack의 특성을 이해하는 것이 중요하다.
유명한 피보나치 수열을 구하는 재귀함수 F(n) = F(n-1) + F(n-2) 의 실행을 생각해 보면, 이 함수는 F(n-1)에서 파생된 모든 스택에 있는 함수와 구문을 처리한 다음, F(n-2) 에서 파생된 스택에 내용을 처리하게 된다.

📍 재귀를 이용한 문제해결

나의 경우, 이해하는 것과 직접해보는 것에 꽤 많은 차이를 느끼는데 그 차이를 줄이는 방법은 많이 해보는 것 밖에 없었다.

문제를 해결 절차는 앞서 설명한 재귀함수 구현 방법을 따르면서, 단순한 문제들을 의식적으로 Reclusion하게 풀어보자.

Problem 1. 1 부터 N까지 합을 구하는 함수를 재귀적으로 작성하시오.

• Step1 - Define a base case

if ( n == 0 ):
    return n

• Step2 - Define a recursive case

sum(n) = n + sum(n-1)

• Step3 - Ensure the recursion terminates

# if sum(0) is called, then recursion terminates

• Step4 - Combine the solution

def reclusiveSum(n):
  if (n == 0):
  	return n
  else:
  	return n + reclusiveSum(n-1)

Problem 2. 회문(Palindrome) 똑바로 읽으나 거꾸로 읽으나 동일한 단어인지 확인하는 함수를 재귀적으로 구현하시오.

• Step1 - Define a base case

# 단어의 길이가 1이거나 0이면 가장 짧은 회문이므로 True 반환
if (len(str) == 0 | len(str) == 1))
	return True
    
# 양 끝이 같지 않으면 회문이 아니므로 False 반환
if ( str[0] != str[-1] )
	return False

• Step2 - Define a recursive case

# 양 끝이 같으면 양 끝을 뺀 문자열로 다시 비교
# 만약, abba 이면 양 끝 a 를 빼고 bb 만 다시 비교
if(str[0] == str[-1]):
	return fun(str[1:-1])

• Step3 - Ensure the recursion terminates

# str = "a" 일때, fun(str) 이 호출되면 재귀함수는 종료 됨

• Step4 - Combine the solution

def isPalindrome(str):

    if(len(str) == 0 | len(str)==1):
        return True
    elif(str[0] == str[-1]):
        return isPalindrome(str[1:-1])
    else:
        return False

Problem 3. Reverse String

• Step1 - Define a base case

# Returns "" if the length of the string is zero.
if (len(str) == 0):
	return ""

• Step2 - Define a recursive case

fun(str[1:]) + str[-1]

• Step3 - Ensure the recursion terminates

# The recursion terminates when the string length is zero.

• Step4 - Combine the solution

def reverseString(str):

	if (len(str) == 0):
		return ""
    else:
    	return reverseString(str[1:]) + str[-1]

Problem 4. decimal to binary conversion

• Step1 - Define a base case

if(number == 1)
	return str(number)
else:
	return ""

• Step2 - Define a recursive case

fun(number//2) + str(number%2)

• Step3 - Ensure the recursion terminates

# If you continue to divide by 2, finally the quotient is either 0 or 1.

• Step4 - Combine the solution

def decimalToBinary(number):
	
    if(number ==1):
    	return str(number)
    elif(number == 0)
    	return ""
    else:
    	return decimalToBinary(number//2) + str(number%2)

📍 마무리

재귀적으로 문제를 풀기위해서는 아래 4가지를 기억하면 된다.

• 재귀적 프로그래밍에는 Recursive Case와 Base Case가 존재한다.
• Base Case는 프로그램을 종료 시키는 역할을 한다.
• 재귀적 호출은 새로운 각각의 함수를 생성하여 스택에 저장하도록 한다.
• 무한 재귀 호출은 실행시 OutOfStackMemory를 이끈다.

Iterative하게 구현하는 것과 다른 건,
스택의 특성을 사용한다는 것과 반복문에서 하던 작업을 스스로 호출을 통해 처리한다는 점이다.

📍 에필로그

Reclusive Programing과 Iterative Programing의 장단점 따위는 신경 쓰고 싶지 않았다. 오로지 구현에만 집중하고 싶었다. 재귀용법 으로 해결 할 수 있는 문제가 얼마나 될까? 하지만 재귀용법을 이해하지 못하면 다음 단계로 가지 못한다. 내가 DFS 문제를 풀때 헤메는 이유. 그 문제의 답을 보아도 이해가 가지 않는 이유가 거기에 있지 않을까?

📍 참고 사이트

• Introduction to Recursion – Data Structure and Algorithm Tutorials
• Python: Recursion - Exercises, Practice, Solution