컴퓨터에서 말하는 자료구조는 컴퓨터에서 자료를 정리하고 조직화하는 다양한 구조를 말한다. 쉽게 설명하자면 효율적으로 데이터를 관리하고 수정, 삭제, 탐색, 저장할 수 있는 데이터 집합을 말한다. 예시로는 스택, 큐, 리스트, 그래프, 트리 등이 있다.
이 자료구조는 어떠한 문제를 처리할때 해당 문제에 로직에 가장 효과적인 자료구조를 찾아서 쓰는 것이 매우 중요하다.
먼저, 자료구조에서 정말 중요한 개념 중 하나인 시간복잡도에 대해 정리해보도록 하겠다.
시간복잡도란?
입력 크기에 대해 어떠한 알고리즘이 실행되는데 걸리는 시간을 말하며 주요 로직의 반복획수를 중점으로 측정됩니다. 이때, 시간을 항상재기보단 어떠한 알고리즘이 주어진 입력크기를 기반으로 어떠한 로직이 몇번 반복되었는가를 중점으로 설명한다.
최선, 평균, 최악의 경우
실행시간은 입력 집합에 따라 다를 수 있음
– 최선의 경우(best case): 수행 시간이 가장 빠른 경우
• 의미가 없는 경우가 많다.
– 평균의 경우(average case): 수행시간이 평균적인 경우
• 계산하기가 상당히 어려움.
– 최악의 경우(worst case): 수행 시간이 가장 늦은 경우
• 가장 널리 사용된다. 계산하기 쉽고 응용에 따라서 중요한 의미를
가질 수도 있다.
– (예) 비행기 관제업무, 게임, 로보틱스
빅오표기법
이러한 시간복잡도에 가장 영향을 많이 끼치는 항의 상수인자를 빼고 나머지 항을 없애서 복잡도를 나타내는 표기법을 빅오 표기법이라고 부른다.
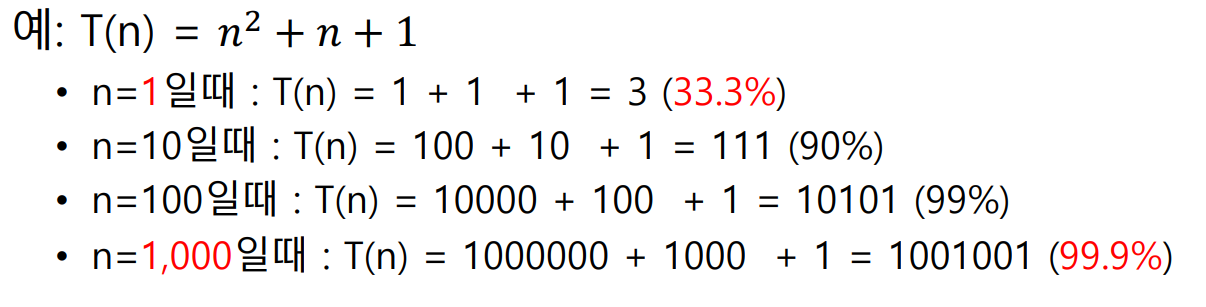
위 예시를 보면 n=100인 경우 T(n) = n^2+ n + 1에서 n^2이 99%의 영향을 주는 것을 볼 수 있다.
빅오표기법 차트로는 n! > 2^n > n^2 > nlogn > n > logn > 1 순이다.
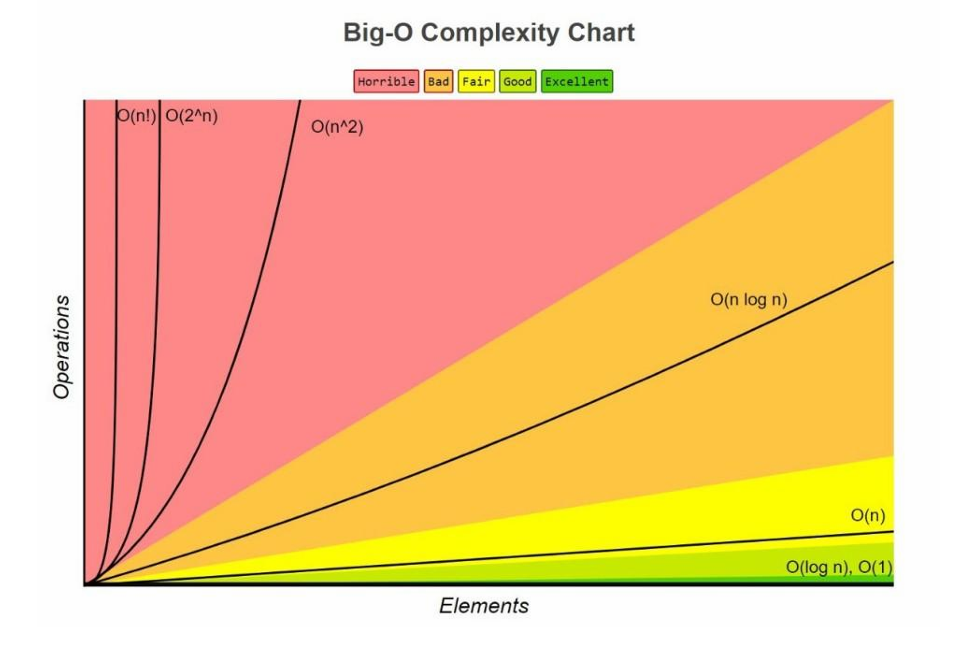
이때, 상수시간의 시간복잡도 O(1)의 경우는 입력크기와 상관없이 일정한 시간복잡도를 가지는 것을 말한다. 보통 입력과 출력, 곱하기, 나누기, 나머지 연산, 빼기, 간단한 if문, 배열의 인덱스 참조등이 O(1)의 시간복잡도를 가진다.
cin, cout, scanf, printf
a[4] -=2;
if(a[0] == 2){
//로직
}
int a[4] = {1,2,5};코드 내에서 시간복잡도를 구하는 방법
for(int i = 0; i < n; i++){
for(int j = 0; j < i; j++){
a += i + j;
}
}해당 이 코드에서 시간복잡도는 어떻게 될까?
형태로 봤을땐 이중 for문이고 외부 반복문에서 i는 0부터 n-1까지 증가한다. 이 반복문은 총 n번 실행된다. 내부 반복문에선, i에 대해 j는 0부터 i-1까지 증가한다. 내부 반복문은 총 i번 실행된다. 실행되는 횟수는 0 + 1 + 2 + 3 + 4 + ... + (n-1)이다. 따라서 등차수열의 합 공식에 따라 1⁄2(n2-n) 이 되기 때문에 시간복잡도는 O(n2)을 가진다.
for (int i = 0; i < N; i++) {
a *= i;
}
for (int j = 0; j < M; j++) {
a *= j;
}이 로직의 시간복잡도는 어떻게 될까?
코드를 보면 for문이 중첩되어있는 것이 아니라 나열되어있다는 것을 알 수 있다. 중첩되어있는 경우엔 각각의 코드에 시간복잡도를 곱해줘야 하지만 나열되어 있는 경우엔 시간복잡도를 더해주면 된다. 따라서 O(N+M)을 시간복잡도라고 할 수 있다.
#include<bits/stdc++.h>
using namespace std;
int n, a[1004], cnt;
int go(int l, int r){
if(l == r) return a[l];
int mid = (l + r) / 2;
int sum = go(l, mid) + go(mid + 1, r);
return sum;
}
int main(){
cin >> n;
for(int i = 1; i <= n; i++){
a[i-1] = i;
}
int sum = go(0, n-1);
cout << sum << '\n';
}이 코드에서는 재귀함수 go가 등장한다. 이 함수는 배열의 구간 합을 계산하는 분할 정복 알고리즘으로 재귀호출의 특성을 잘 이해해야 한다. 재귀함수를 많이 공부해보신 분들은 아시겠지만, 순차적으로 go(idx -1) go(idx+1)과 같은 구조를 가진 재귀함수는 보통 호출이 2번 일어나면 2n, 3번 일어나면 3n이라고 보면 되지만, 이러한 구조를 가지지 않은 예를 들어 go(idx/2)로 호출되는 경우는 O(N)을 가진다. 하지만 이렇게 외우는 것도 좋지만 자세히 차근차근 봐보도록 하겠다.
먼저 go 함수는 배열의 왼쪽 구간과 오른쪽 구간의 합을 재귀적으로 계산하는데 l==r이면 a[1]을 반환하고 그게 아니라면 중간지점 mid를 계산후, 왼쪽 부분 합 go(l,mid)와 오른쪽 부분 합 go(mid + 1,r)을 더해준다.
n=1일때 go(0,0) 호출 횟수는 1이고, n=2일때, go(0, 1) go(0, 0) go(1, 1)으로 호출횟수는 3이고 n=3일때, go(0, 2) go(0, 1) go(0, 0) go(1, 1) go(2, 2)로 호출횟수는 5이다. 이러한 패턴을 보면 각 n에 대해 2n-1호출이 이루어지는 것을 알수있다. 상수와 작은 항을 무시하면 O(n)이 시간복잡도라는 것을 알 수 있다.
공부를 하면서 배운건데 재귀함수의 시간복잡도를 구할땐 재귀함수의 main logic * 함수 호출횟수는 재귀함수의 시간복잡도를 나타낸다는 것을 알게되었다. 유용한 꿀팁인것 같아 꼭 기억하고 있으면 좋을 것 같다.
이렇게 3가지 코드를 보면서 시간복잡도를 구하는 방법을 알아보았다. 시간복잡도는 효울적인 코드를 만드는데 기준이 되고, 시간복잡도를 생각하면서 코드를 짜다보면 시간복잡도를 줄여나가면서 성능을 더욱 향상시킬 수 있게된다. 시간 복잡도를 이해하고 분석하는 능력은 더 나은 알고리즘을 설계하고 최적화하는 데 필수적이기 때문에 앞으로 코드를 작성할 때 항상 시간 복잡도를 염두에 두어야겠다.