[프로그래머스] 격자 뒤집기 미로 (JavaScript)

문제 설명[링크]

세로 길이가 n, 가로 길이가 m인 직사각형 모양의 격자판이 있습니다. 가장 왼쪽 위 격자의 좌표는 (1, 1)이고, 가장 오른쪽 아래 격자의 좌표는 (n, m)입니다.

각 격자의 양면에는 자연수가 적혀있습니다. 초기 상태에서는 각 격자의 한 면만이 보이도록 놓여 있습니다.

당신은 아래의 행동을 원하는 만큼 수행할 수 있습니다. 행동을 한번 수행할 때마다 비용 k가 소모됩니다.

격자판의 하나의 행 혹은 하나의 열에 존재하는 모든 격자를 뒤집어 보이는 면과 숨겨진 면을 교체할 수 있습니다.
모든 행동을 마친 후, (1, 1) 격자에 위치한 말을 (n, m) 격자까지 이동하면서 방문한 격자들의 보이는 수를 점수에 더합니다. 말을 이동할 때는 상하좌우로 인접한 격자로만 이동할 수 있으며, 한번 방문한 격자는 다시 방문할 수 없습니다.

이때, 말을 이동시켜 얻을 수 있는 점수 총합 - 총 비용의 최댓값을 구하려고 합니다.

예를 들어, 아래 그림과 같이 n = 2, m = 2인 격자판이 있고, k = 0이라고 가정해 보겠습니다.

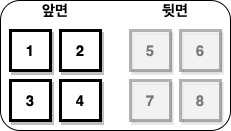
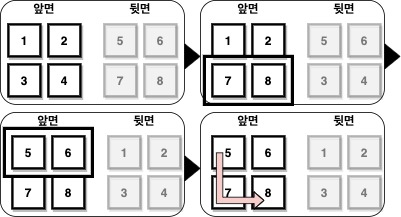
아래와 같이 첫 번째 행과 두 번째 행을 뒤집고 말을 (5 → 7 → 8)과 같이 이동시키면 점수 총합은 20이고 총 비용은 0이며, 이때가 점수 총합 - 총 비용이 최대입니다.

각 격자의 현재 보이는 면에 적힌 수를 나타낸 2차원 정수 배열 visible과, 숨겨진 면에 적힌 수를 나타낸 2차원 정수 배열 hidden이 매개변수로 주어집니다. 점수 총합 - 총 비용의 최댓값을 return 하도록 solution 함수를 완성해 주세요.

풀이

• 행, 열의 개수 둘 중 하나라도 홀수이면 모든 판 다 돌수 있음(각 VALUE가 양수이므로 도는게 이득)
• 짝수인경우, i + j가 짝수인칸 중 제일 작은칸 제외하면됨
• 세로줄 n 최대값이 14이고, 2^14 는 약 1~2만 이므로 다항시간안에 순회 가능
• 2^14 경우 모두 순회하면서 greedy하게 세로줄 뒤집는 경우 계산

function calculate(matrix, hidden, n, m, k, isAllEven) {
  const colSum = new Array(m).fill().map(() => new Array(2).fill(0));
  for (let i = 0; i < n; i++) {
    for (let j = 0; j < m; j++) {
      colSum[j][0] += matrix[i][j];
      colSum[j][1] += hidden[i][j];
    }
  }

  let res = 0;
  for (let i = 0; i < m; i++) {
    res += Math.max(colSum[i][0], colSum[i][1] - k);
  }

  if (isAllEven) {
    let min = Infinity;
    for (let i = 0; i < n; i++) {
      for (let j = 0; j < m; j++) {
        if ((i + j) % 2 === 0) continue;
        let val;
        if (colSum[j][0] === colSum[j][1] - k) {
          val = Math.min(matrix[i][j], hidden[i][j]);
        } else if (colSum[j][0] > colSum[j][1] - k) {
          val = matrix[i][j];
        } else {
          val = hidden[i][j];
        }

        min = Math.min(min, val);
      }
    }

    res -= min;
  }

  return res;
}

function solution(visible, hidden, k) {
  const n = visible.length; // 1 ~ 14
  const m = visible[0].length; // 2 ~ 100
  const isAllEven = n % 2 === 0 && m % 2 === 0;

  const cases = 1 << n;
  let res = 0;
  for (let i = 0; i < cases; i++) {
    let cost = 0;
    for (let j = 0; j < n; j++) {
      if (i & (1 << j)) {
        [visible[j], hidden[j]] = [hidden[j], visible[j]];
        cost += k;
      }
    }

    res = Math.max(res, calculate(visible, hidden, n, m, k, isAllEven) - cost);

    for (let j = 0; j < n; j++) {
      if (i & (1 << j)) {
        [visible[j], hidden[j]] = [hidden[j], visible[j]];
      }
    }
  }

  return res;
}