문제
빨간색 볼과 파란색 볼이 <그림 1>에서 보인 것처럼 일직선상에 섞여 놓여 있을 때, 볼을 옮겨서 같은 색 볼끼리 인접하게 놓이도록 하려고 한다. 볼을 옮기는 규칙은 다음과 같다.
- 바로 옆에 다른 색깔의 볼이 있으면 그 볼을 모두 뛰어 넘어 옮길 수 있다. 즉, 빨간색 볼은 옆에 있는 파란색 볼 무더기를 한 번에 뛰어 넘어 옮길 수 있다. 유사하게, 파란색 볼은 옆에 있는 빨간색 볼 무더기를 한 번에 뛰어 넘어 옮길 수 있다.
- 옮길 수 있는 볼의 색깔은 한 가지이다. 즉, 빨간색 볼을 처음에 옮겼으면 다음에도 빨간색 볼만 옮길 수 있다. 유사하게, 파란색 볼을 처음에 옮겼으면 다음에도 파란색 볼만 옮길 수 있다.
예를 들어, 처음에 볼이 <그림 1>에서 보인 것처럼 있을 때, 빨간 볼을 <그림 2>에서 보인 것처럼 옮긴 후, <그림 3>에서 보인 것처럼 옮긴다면 두 번 만에 같은 색끼리 모을 수 있다.
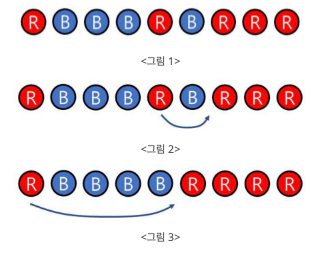
반면에 파란색 볼을 선택하여 에서 보인 것처럼 옮기면(화살표에 있는 수는 옮기는 순서를 나타낸다) 네 번을 옮겨야 같은 색의 볼끼리 모을 수 있다

일직선상에 놓여 있는 볼에 관한 정보가 주어질 때, 규칙에 따라 볼을 이동하여 같은 색끼리 모으되 최소 이동횟수를 찾는 프로그램을 작성하시오.
입력
첫 번째 줄에는 볼의 총 개수 N이 주어진다. (1 ≤ N ≤ 500,000) 다음 줄에는 볼의 색깔을 나타내는 문자 R(빨간색 볼) 또는 B(파란색 볼)가 공백 없이 주어진다. 문자열에는 R 또는 B 중 한 종류만 주어질 수도 있으며, 이 경우 답은 0이 된다.
출력
최소 이동횟수를 출력한다.

N = int(input())
S = input()
# 빨간색 count 저장
red = S.count('R')
# 파란색 count 저장
blue = N - red
# 빨강, 파랑 중 더 개수가 적은 것 저장
ans = min(red, blue)
cnt = 0
#반복문 돌면서, 연속적인 것 count
for i in range(N):
if S[i] != S[0]:
break
cnt += 1
# 만약에 연속 count한게 빨간색이었다면, 위의 답 vs <전체 빨강 개수 - 앞에서부터 연속 빨강 개수> 중 적은 것 저장
if S[0] == 'R':
ans = min(ans, red - cnt)
# 만약에 연속 count한게 빨간색이었다면, 위의 답- <전체 파랑 개수 - 앞에서부터 연속 파랑 개수> 중 적은 것 저장
else:
ans = min(ans, blue - cnt)
cnt = 0
# 반복문 거꾸로 돌면서 끝에서 얼마나 연속되는지 저장
for i in range(N-1, -1, -1):
if S[i] != S[N - 1]:
break
cnt += 1
#만약 연속 count했던게 빨강이었다면, 위의 값 vs <전체 빨강 개수 - 뒤에서부터 연속 빨강 개수>
if S[N - 1] == 'R':
ans = min(ans, red - cnt)
#만약 연속 count했던게 파랑이었다면, 위의 값 vs <전체 파랑 개수 - 뒤에서부터 연속 파랑 개수>
else:
ans = min(ans, blue - cnt)
print(ans)
# 최소값을 구하기 위해서 계속해서 mid으로 답을 갱신해나간다.
우선순위
- <둘 중 최소> -> 빨강 개수 vs 파랑 개수
- <둘 중 최소> -> 1번 vs "전체 빨강/파랑 개수 - 앞에서부터 세었을 때 연속된 빨강/파랑 개수"
- <둘 중 최소> -> 2번 vs "전체 빨강/파랑 개수 - 뒤에서부터 세었을 때 연속된 빨강/파랑 개수"
전체 빨강/파랑 개수에서 앞/뒤에서 연속된 빨강/파랑 개수를 빼는 이유:
- 끝에서부터 연속되어 있다면 그 볼 무더기는 움직일 필요가 없는것들이고, 따로 떨어진것들만 무더기쪽으로 움직이면 되어서 이게 곧 횟수를 의미
