[프로그래머스/탐욕법(Greedy)] Level 2 | 조이스틱 (JavaScript)

ain·2023년 6월 17일
JavaScript그리디프로그래머스
4

알고리즘

목록 보기
1/1
post-thumbnail

풀이는 bbeyak님의 풀이와 rio(리우)님의 풀이를 참고하였습니다.

문제 설명

조이스틱으로 알파벳 이름을 완성하세요. 맨 처음엔 A로만 이루어져 있습니다.
ex) 완성해야 하는 이름이 세 글자면 AAA, 네 글자면 AAAA

조이스틱을 각 방향으로 움직이면 아래와 같습니다.

▲ - 다음 알파벳
▼ - 이전 알파벳 (A에서 아래쪽으로 이동하면 Z로)
◀ - 커서를 왼쪽으로 이동 (첫 번째 위치에서 왼쪽으로 이동하면 마지막 문자에 커서)
▶ - 커서를 오른쪽으로 이동 (마지막 위치에서 오른쪽으로 이동하면 첫 번째 문자에 커서)

예를 들어 아래의 방법으로 "JAZ"를 만들 수 있습니다.

  • 첫 번째 위치에서 조이스틱을 위로 9번 조작하여 J를 완성합니다.
  • 조이스틱을 왼쪽으로 1번 조작하여 커서를 마지막 문자 위치로 이동시킵니다.
  • 마지막 위치에서 조이스틱을 아래로 1번 조작하여 Z를 완성합니다.
    따라서 11번 이동시켜 "JAZ"를 만들 수 있고, 이때가 최소 이동입니다.

만들고자 하는 이름 name이 매개변수로 주어질 때, 이름에 대해 조이스틱 조작 횟수의 최솟값을 return 하도록 solution 함수를 만드세요.

제한사항

  • name은 알파벳 대문자로만 이루어져 있습니다.
  • name의 길이는 1 이상 20 이하입니다.

입출력 예

namereturn
"JEROEN"56
"JAN"23


문제 해석

우리는 처음에 A로만 이루어져있던 문자를 인자로 들어온 알파벳 이름으로 바꿔주는게 목표이다.
이름 길이 만큼 A로 이루어져 있는데, 예를 들면 이름을 JAZ으로 바꿔야 할 때 처음에 AAA로 이루어진 문자열이 표시되고 이를 이름으로 바꿔줘야 한다.

🕹️ -> 이 조이스틱으로 커서를 조작해야 하는데 조작횟수를 최소한으로 하여 이름을 만들어야 한다.
이름을 만드는데 필요한 조작은 두가지이다.

  1. 알파벳을 바꿔줄 때 조이스틱을 위로 움직여 알파벳 순으로 움직이거나, 아래로 움직여 알파벳 반대순으로 움직인다.

  2. 조이스틱을 오른쪽으로 움직여 다음 알파벳으로 넘어가고, 왼쪽으로 움직여 마지막 알파벳으로 이동한다.
    예를 들어, 우리가 바꿔줘야할 이름이 JAZ이라면,

    • A에서 J까지 아홉 번 조작(BCDEFGHIJ)
    • 왼쪽으로 조작하여 마지막 알파벳으로 이동할 때 한 번 조작
    • 마지막 알파벳을 Z으로 바꿔줄 때 A에서 Z로 알파벳 반대순으로 이동하여 한 번 조작
      총 열한 번 조작이 된다.

여기서 두 번째 A로 이동하지 않고 마지막으로 이동한 이유는 A는 알파벳 조작을 해줄 필요가 없기 때문에, A를 마주쳤을때 A를 통과하거나 뒤로 돌아갈 수 있는 선택지가 주어진다.

만약, 첫 번째 알파벳에서 두 번째 알파벳인 A를 통과하여 세번째로 간다면, 이동하는데 두 번의 조작이 필요하지만 첫 번째 알파벳에서 A를 거치지 않고 바로 마지막 알파벳으로 돌아간다면 한 번의 조작만 필요하다.

그림으로 설명해보자면 이런식이다.
조이스틱의 움직임을 화살표로 표시했고, 파란 박스는 cursor(커서), 초록색 +{숫자}로 조작 횟수를 나타내보았다. ↓
JAZ 그림으로 설명
그림 출처: 본인

접근 시도

접근을 해보긴 해봤는데...

  // 첫번째 문자부터 차례대로 조작한다.
  // 첫번째 문자가 A인 경우 반대편으로 간다.
  // 오른쪽으로 가는게 최선인 경우는 현재 커서가 문자열의 앞부분에 있을 경우.(i < Math.floor(name.length / 2))
  // 왼쪽으로 가는게 최선인 경우는 현재 커서가 문자열의 뒷부분에 있을 경우. i >= Math.floor(name.length / 2)
  // 26개 알파벳중에 13(78N) 이전 알파벳이면 위로 가고 이후 알파벳이면 아래로 간다.

나중에 정답을 보니 접근을 잘못 한 듯 하다.



풀이

function solution(name) {
  var answer = 0;
  let min = name.length - 1;

  for (let i = 0; i < name.length; i++) {
    let currentAlphabet = name.charCodeAt(i);

    if (currentAlPhabet < 78) {
      answer += currentAlphabet % 65;
    } else {
      answer += 91 - currentAlphabet;
    }

    let nextIndex = i + 1;

    while (nextIndex < name.length && name.charCodeAt(nextIndex) === 65) {
      nextIndex += 1;
    }
    min = Math.min(
      min,
      i * 2 + name.length - nextIndex, // 먼저 오른쪽으로 가기
      i + (name.length - nextIndex) * 2 // 처음부터 반대로 가기
    );
  }
  answer += min;
  return answer;
}


실제 접근 방법 (풀이 설명)

  1. 최종 목표는 알파벳 이동 횟수 + 커서 이동 횟수를 누적하여 반환하는 것이다.
  2. 커서는 첫번째 문자부터 시작한다.
  3. 문자열에 A가 없다면 문자열 길이 - 1가 최소 횟수이다. (첫번째 문자에 커서가 있는 상태이기 때문에 마이너스 1을 해야 함)
let min = name.length -1
  1. 따라서, 문자열에 A가 포함되어있을 때는 커서가 A를 거치는 식이 빠를지, 오른쪽으로 조작하여 A 직전까지 갔다가 돌아가는게 빠를지, 아예 처음부터 왼쪽으로(뒤로) 갔다가 앞으로 돌아오는게 빠를지 비교를 해야한다.
  2. 알파벳을 조작할 때에는 간단하다.
    26개의 알파벳중 정 가운데에 있는 13번째 알파벳인 N을 기준으로, N보다 작으면 (A~M) 알파벳순으로 조작하는게 빠르고, N보다 크거나 같으면 (N~Z) 알파벳 반대순으로 조작하는게 빠르다.
for (let i = 0; i < name.length; i++) {
  let currentAlPhabet = name.charCodeAt(i);
  // 반복문을 돌면서 현재 커서가 위치한 알파벳이 N보다 작으면 [커서가위치한알파벳]과 [A]사이를 얼만큼 이동해야 하는지를 계산해준다.
  if (currentAlPhabet < 78) { // 78은 N의 아스키코드
    // 나눈 후 나머지로 계산해줘도 되고, else문안의 코드처럼 빼기를 해주어도 된다.
    answer += currentAlPhabet % 65; // 65는 A의 아스키 코드
  } else {
    // 현재 커서가 위치한 알파벳이 N보다 크면 [Z]와 [커서가위치한알파벳]사이를 얼만큼 이동해야 하는지를 계산해준다.
    answer += 91 - currentAlPhabet; // 91은 Z의 아스키 코드
  }
}
  1. 알파벳 조작을 할때에는 N을 중심으로 하였듯, 커서를 이동할 때에는 A 친구들을 기준으로 앞의 문자들에서 커서를 조작할 횟수가 더 많은지, 마지막 문자로 이동하여 조작할 횟수가 더 많은지 봐야한다.
    그 전에, 현재 커서가 위치한 알파벳 다음으로 A 친구가 오는지 확인하고, A 친구의 바로 뒤의 오는 인덱스를 알아낸다.
let nextIndex = i + 1; // A의 뒤 인덱스를 찾을 nextIndex

// 현재 커서가 위치한 알파벳의 다음 알파벳이 A인지 확인한다. A면 nextIndex에 1을 더해준다.
// 만약 JAZ라면 0번째 인덱스인 J 뒤에 A가 하나 있기 때문에 nextIndex는 2가 되어있을테고 2번째 인덱스는 Z이다.
// 이 nextIndex는 나중에 [문자열길이] - [nextIndex]를 하여 마지막 A 뒤에 오는 알파벳 수를 알아낼 수 있다.
while (nextIndex < name.length && name.charCodeAt(nextIndex) === 65) {
  nextIndex += 1;
}

이제 최소로 조작하는 횟수를 찾아내야하는데, [처음에 A를 거쳐서 쭉 이동했던 횟수]와 [ 오른쪽으로 이동했을 때의 횟수], [처음부터 반대로 갔을 때의 횟수] 이 세가지를 비교한다.

min = Math.min(
  min, // 그냥 오른쪽으로 쭉 가는 횟수
  i * 2 + name.length - nextIndex, // 먼저 오른쪽으로 가기
  i + (name.length - nextIndex) * 2 // 처음부터 반대로 가기
);

이게 대체 뭔 소리냐하면!

예시를 들어보겠다.



비교 예시

A 친구들
이 사진에서 MONAAAJOE 비교를 해보자. A 친구들 세명이 있다고 치고 우선 이들을 투명인간 취급해준다.

  • M에서 A 직전까지 가는데 두 번, 뒤로 돌아가기 위해서 다시 M까지 가는데 두 번, 뒤로 돌아가서 A 직전까지 가는데(JOE) 세 번의 조작이 필요하다. 총 일곱 번의 조작이 필요하다.

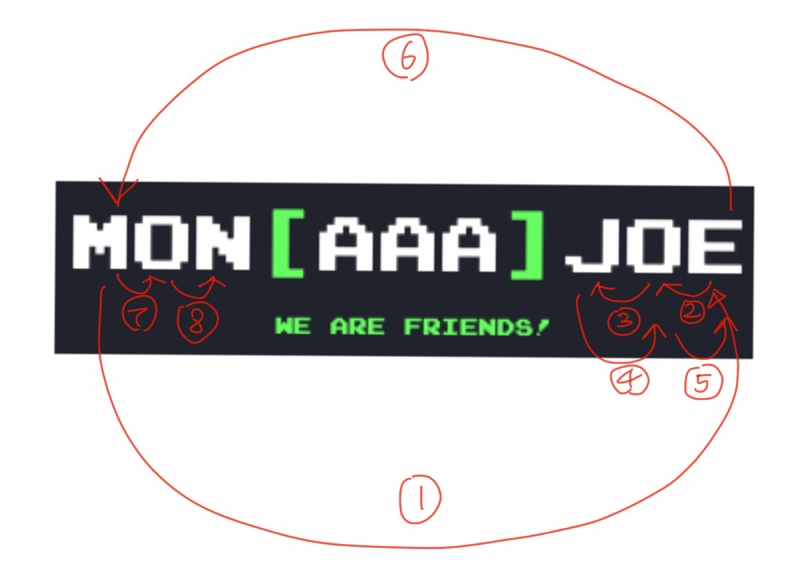
  • 반대로, M에서 바로 마지막 문자로 이동하여 세번째 A의 직전인 J로 가보자. 그러면 세 번의 조작이 필요하다. 다시 MON을 세기 위해서 처음 문자인 M으로 돌아오는데만 세 번의 조작이 필요하다. 그리고 다시 첫번째 A직전까지 세면 두 번의 조작이 필요하여 총 여덟번의 조작이 필요하다.

  • 마지막으로, A를 거쳐서 오른쪽으로 쭉 커서를 조작하면 여덟번의 조작이 필요하다. 그래서 결론은 MONAAAJOE는 앞에서 먼저 돌고, 마지막 문자열로 가야 최소한의 횟수로 조작할 수 있다.

M -> O -> N -> O -> M -> E -> O -> J 가 커서 조작 횟수가 적다!

여기까지 비교하는 예시였다.



이걸 어떻게 연산 할 것인가?

오른쪽으로 먼저 커서를 조작했을 때

  • 우선, A 친구들 왼쪽에 있는 MON에서는 M에서 N으로, 다시 N에서 M으로 돌아오는데까지 4번의 조작이 필요하다.
  • 첫번째 A의 직전 알파벳인 N의 인덱스는 2이다. 이 인덱스 곱하기 2를 하면 A 직전까지 갔다가 다시 돌아오는 횟수를 구할 수 있다. (왔다 -> 한번, 갔다 -> 두번 그래서 곱하기 2)
  • 앞에서 가져온 횟수 더하기 A 친구들 뒤에있는 알파벳의 수를 하면 결과가 나온다.
i * 2 + name.length - nextIndex
// `A` 앞의 알파벳 수 => i
// 왔다갔다 해야하는 횟수 => 2
// `A` 뒤의 알파벳 수 => name.length - nextIndex

처음부터 거꾸로 이동하여 조작했을 때

  • 첫번째 알파벳부터 시작해서 문자열의 맨 마지막으로 이동한 후, 마지막 A뒤에 있는 알파벳까지 돌고, 다시 문자열의 첫번째 알파벳으로 돌아오는 횟수는:
  • 마지막 A 뒤에 있는 알파벳의 수에 2를 곱하여 왔다갔다 하는 수를 구할 수 있다.
  • A 친구들 뒤에 있는 알파벳에 다녀오는 수는 구했으니 A 친구들 앞에 있는 알파벳을 더해주면 결과가 나온다.
i + (name.length - nextIndex) * 2
// `A` 앞의 알파벳 수 => i
// `A` 뒤의 알파벳 수 => name.length - nextIndex
// 왔다갔다 해야하는 횟수 => 2

이상으로, 프로그래머스 자그마치 레벨 2의 Greedy 탐욕법 문제, 조이스틱의 (내 나름대로) 해석이였다...



코드 + 주석

function solution(name) {
  var answer = 0;
  // 뒤로 돌아가지 않고 조작했을 때의 최소 횟수는 [문자 length - 1]
  // 처음 알파벳부터 다음 알파벳으로 넘어가는 조작 횟수부터 시작하니 length - 1
  // 예를 들어 길이가 3인 문자면 1->2로 이동하는 할 때 +1, 2->3으로 이동할때 +1이기 떄문에 length - 1을 해줘야 함.
  let min = name.length - 1;

  for (let i = 0; i < name.length; i++) {
    let currentAlPhabet = name.charCodeAt(i);

    // 현재알파벳이 N(26개 알파벳에서 13번째 알파벳)보다 작으면(A~M) 뒤로 돌아갈때가 앞으로 가는것보다 빠름.
    // 이동하는 만큼의 조작 횟수를 answer에 저장. (여기서 마이너스를 해도 되고 나눈 후의 나머지로(%) 계산 해도 된다.)
    if (currentAlPhabet < 78) {
      answer += currentAlPhabet % 65;
    } else {
      // N보다 크거나 같으면(N~Z)
      // A부터 시작해서 조작해야하는데 뒤로 돌아가기 때문에 A를 제외하고 Z부터 세기 때문에 Z - 현재알파벳을 계산.
      answer += 91 - currentAlPhabet;
    }

    // i의 다음 인덱스가 A이면 하나의 혹은 연속된 A 다음에 오는 알파벳의 인덱스를 가리킨다.
    let nextIndex = i + 1;

    // 현재알파벳이 마지막 알파벳이 될 때까지 && 다음알파벳으로 A가 나올때까지 nextIndex += 1
    // nextIndex가 A가 아니면 넘어가고, nextIndex에 A가 나온다면 nextIndex += 1을 하여 A의 다음 인덱스도 A인지 확인한다.
    // -> 다음 문자열들에서 A를 찾는 작업
    while (nextIndex < name.length && name.charCodeAt(nextIndex) === 65) {
      nextIndex += 1;
    }

    // length - nextIndex는 뒤로 쭉 갔을 때의 길이(A를 통과해서 갔을 때).
    min = Math.min(
      min,
      i * 2 + name.length - nextIndex, // 먼저 오른쪽으로 가기
      // 이 경우는 A의 앞에 있는 알파벳들이 뒤에 있는 알파벳의 수보다 적을 경우 최소가 된다.
      // 앞에서 갔다가 뒤돌아오는 횟수 (A 뭉떵이를 기준으로 앞에 알파벳 < 뒤에 알파벳일 때 앞에서 A 직전까지 갔다가 다시 돌아오기 때문에 곱하기 2를 해준다.)
      // 예를 들어 CDAAJJJJ이면 JJJJ보다 CD가 짧기 때문에 D로 갔다가 다시 뒤돌아서 마지막인 J로 가야한다.
      // C에서 D까지 조작해서 +1, 다시 D에서 C로 되돌아갈 때 + 1, 따라서 i * 2를 해줘야 한다.
      // 여기서 [문자열의 길이]에서 [마지막에 위치한 A의 바로 뒤에 있는 문자의 인덱스]를 빼주면 A 뒤에 있는 알파벳들의 길이를 구할 수 있다. 예시에서는 JJJ이기 때문에 3.
      i + (name.length - nextIndex) * 2 // 처음부터 반대로 가기
      // 이 경우는 A의 앞에 있는 알파벳들보다 뒤에 있는 알파벳들의 수가 적을 경우 최소가된다.
      // 예를 들어, JJJJAACD 일 때, A의 앞에 문자열이 뒤보다 많기 때문에
      // 네번째 J까지 갔다가 다시 앞으로 돌아가는것(8회)보다 처음부터 CD를 돌고 다시 JJJJ로 돌아가는게 횟수가 적다(7회)
    );
  }
  answer += min;
  return answer;
}

참고

profile
ain
프론트엔드 개발 연습장 ✏️ 📗

0개의 댓글