스탠포드 강의의 CS231n 2강을 보고 정리한 내용입니다.
링크 : https://www.youtube.com/watch?v=OoUX-nOEjG0
Image Classification
이미지 분류는 컴퓨터 비전 분야의 핵심 과제이다. 이미지를 분류하기 위해선 먼저 이미지를 인식해야 한다. 사람의 경우 고양이 이미지를 보았을 때 고양이의 뾰족한 귀, 얼굴 생김새, 털모양 등의 수많은 특징들을 통합적으로 파악함으로써 고양이임을 파악한다. 하지만 컴퓨터의 경우 모든 것을 숫자로 인식한다. 구체적으로는 아래의 슬라이드에서 확인할 수 있듯이 픽셀 단위로 0 ~ 255 범위의 숫자로 사진을 인식한다.
그렇기 때문에 사람과 같이 사진을 그 자체로 인식할 때 발생하지 않았던 어려움들이 생긴다. 만일 바라보는 시점의 차이, 조명, 평소와 다른 상태의 자세, 숨겨짐, 어지러운 배경 등의 변화가 발생한다면, 각 픽셀의 숫자가 완전히 바뀌게 된다.
좋은 classifier란 어떤 특성이 필요할까? 위에서 언급한 변화들에 둔감하면서도 다른 class와는 구분이 될 정도의 민감함이 있어야 할 것이다.
Classifier를 만들어보자. 가장 먼저 떠올릴 수 있는 아이디어는 사람이 사물을 인식하는 방법이다. 앞서 사람들은 여러 특징들을 종합적으로 고려하여 이미지를 인식한다고 했었다. 코드 상으로 여러 특징들을 함수화해서 저장하는건 어떨까?
뭔가 가능할 듯 싶지만 조금만 더 생각해보면 불가능하다. 정확히 몇 개의 어떤 특성들을 지정해줘야할지 정의하기 힘들다. 고양이를 예시로 들어봐도 뾰족한 귀, 털의 모양 등 수많은 특징들이 있다. 설령 오랜 작업 끝에 특징들을 정의했다 하더라도 새로운 클래스가 생길 때마다 처음부터 다시 특징들을 정의해야 한다. 비효율적이다. 어찌보면 당연한 결과다. 사람과 컴퓨터는 인식 체계가 다른데 같은 원리로 분류한다는 건 상식적으로 말이 안된다. 접근 방법을 바꿔서 Data driven approach를 도입해보자. 질로 승부할 수 없다면 양으로 승부하자는 말을 떠올리면 이해하기 쉽다. Data driven approach란 특징들을 일일이 정의해주는 대신 수많은 데이터를 입력해서 컴퓨터가 스스로 특징들을 파악할 수 있도록 하는 방법이다.
- Data driven approach
- 이미지와 라벨이 있는 dataset을 모은다.
- 머신러닝으로 classifier를 학습시킨다.
- 새로운 이미지로 classifier를 평가한다.

Classifier 1 : K Nearest Neighbor
K nearest neighbor 방법은 거의 사용하지 않는 방법이지만 classifier의 개념을 직관적으로 이해하는 데에 도움이 되기 때문에 처음에 소개한다. Classifier의 분류 과정은 크게 두 단계(train, test)로 나눌 수 있다. K Nearest Neighbor의 경우 train 단계에선 모든 데이터와 라벨을 저장한다. Test 단계에선 train 단계에서 저장된 모든 이미지들과 test 단계의 이미지들을 일일이 비교해본 후 가장 유사한 이미지의 class로 분류한다. 따라서 train 단계에서 소요되는 시간은 거의 없고(이미지를 로딩하는 시간을 제외하곤) test 단계에서 상당히 많은 시간이 소요된다. 하지만 우리가 원하는 classifier는 train 단계에서 많은 시간이 소요되더라도 test 단계에서 시간을 거의 소요하지 않는 것이다. 그 이유는 classifier를 실생활에서 사용할 때 즉각적으로 판단을 하는 것을 원하기 때문이다. 여기에서 K nearest neighbor classifier가 잘 사용되지 않는 이유를 알 수 있다.

앞서 일일이 이미지를 비교한다고 했는데 구체적으로 비교하는 방법이 뭘까? train 이미지와 test 이미지의 픽셀을 비교해준다.
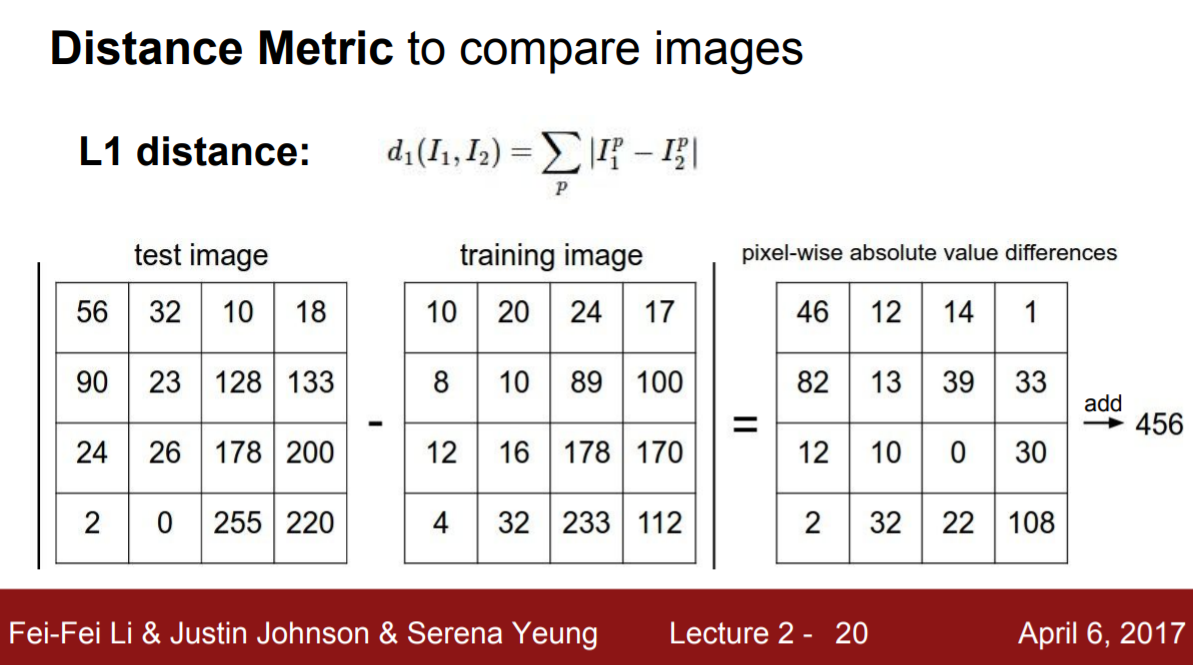
hyperparameter 1 : distance metric
픽셀 간 거리 측정 방법에 두 가지가 있는데 L1 distance와 L2 distance가 있다. L1 distance는 좌표에 dependent하지만 L2 distance는 좌표에 independent하다는 특징이 있다. 좌표에 dependent 하다는 것은 좌표에 의미가 있다는 것이므로 지정된 특성을 이용할 때 L1을 사용한다. L2는 좌표에 independent하기 때문에 특성을 모를 때 사용한다. 각자 쓰임새를 아는 것이 중요한 이유는 distance metric이 모델을 학습하기 전에 설정하는 hyperparameter이기 때문이다. (모델이 학습을 통해 얻는 값들에 대한 변수는 parameter이다.)

hyperparameter 2 : K
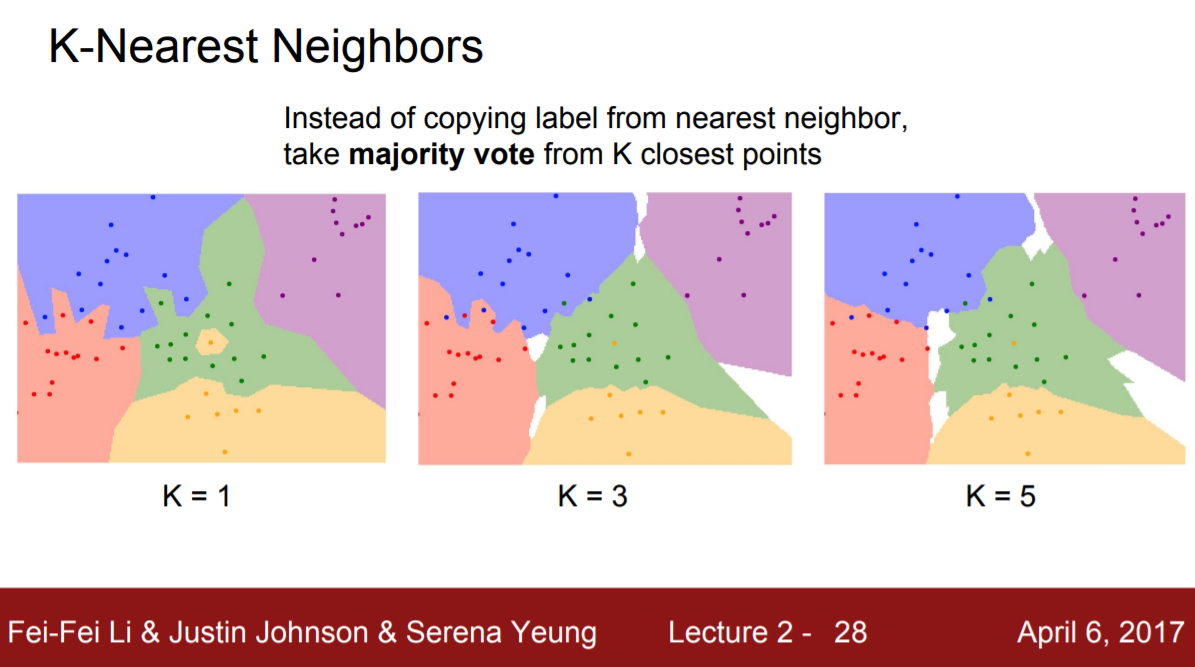
K란 1개의 가장 가장 가까운 이미지가 아닌 여러 K개의 이미지를 고려해서 decision boundary를 설정하기 위한 hyperparameter이다. K에 높은 숫자를 대입할수록 decision boundary가 부드러워지는 것을 밑의 슬라이드에서 확인할 수 있다. 그렇다면 왜 1보다 큰 K를 설정하려고 할까? K = 1일 때를 보면 초록색 영역 가운데에 오렌지 점이 있는 것을 알 수 있다. 그렇다고해서 decision boundary가 중앙 부분에서 오렌지 색으로 바뀌는 것은 바람직하지 않다. 예외적으로 발생된 상황일 가능성이 높기 때문이다. 따라서 K =1일 때는 training data에 overfitting되었다고 짐작한다. 결국 중요한 것은train data에 맞게 fit하는게 아닌 test data(새로운 데이터)에 잘 맞게 fit하는 것이므로 generalization이 중요하다. 따라서 K > 1인 값, 주로 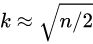
으로 설정해준다. 여기서 주의할 점은 K가 너무 커지면 underfitting이 발생한다는 점이다. 따라서 여러번의 시행착오를 통해 최적의 k를 경험적으로 찾아줘야 한다. Generalization은 모델 학습 시 핵심 개념으로 3강에서는 generalization을 위한 기법으로 regularization을 배운다.
hyperparameter tuning
어떻게 최적의 hyperparameter를 찾을까? 앞서 말한대로 distance metric은 특성의 지정 여부, k는 √(n/2)로 설정한다고 팁을 주었지만 팁은 처음에 값을 어떻게 설정할지에 대한 방향 설정에 도움이 될 뿐, 가장 좋은 성능을 도출해내는 hyperparameter가 아니다. 최적의 hyperparameter를 구하기 위해선 직접 해보면서 결정할 수 밖에 없다. 직접 해볼 때, 데이터를 train, validation, test set으로 나누어야한다. 이중 Validation set에서 hyperparameter tuning을 진행한다.

Test set은 모델의 성능을 평가하기 위해 존재하는 set으로, training된 모델이 새로운 데이터에 적용되었을 때 성능이 어떠한지 평가하기 위해 존재한다. 따라서 마지막에 단 한번 사용한다. 그러한 이유로 test set에서 hyperparameter tuning이 이뤄지지 않는다.
그렇다면 Training set와 Validation set의 차이는 무엇이고 왜 validation set에서 hyperparameter tuning을 진행할까? Training set은 라벨 정보(정답)에 대한 접근성이 있는 반면에 validation set은 라벨 정보에 대한 접근성이 없다. 데이터셋에 물론 라벨 정보가 존재하지만 알고리즘이 잘 작동하는지 체크할 때만 사용한다. 쉽게 말하자면, validation set은 hyperparameter tuning을 위해 train set의 일부를 떼와서 test set에 넣기 전 test set과 유사한 기능을 할 수 있도록 만든 것이다.
Classifier 2: Linear Classifier
KNN 알고리즘은 test set을 train set에 있는 모든 사진들과 하나씩 비교하면서 가장 비슷한 사진을 찾기 때문에 비효율적이었음을 확인했다. 그렇다면 하나씩 비교하지 않고 클래스별로 하나의 템플릿을 만들어 test set을 그 템플릿과만 비교를 한다면 훨씬 효율적이지 않을까? 이 방법을 쓴 분류기가 바로 linear classifier이다.

위 슬라이드를 보면 CIFAR10 자료의 10개의 클래스별로 하나의 템플릿을 생성한 것을 확인할 수 있다. 여기서 문제점이 생기는데 각 클래스에 속한 모든 사진들을 평균내기 때문에 말의 경우 머리가 양쪽으로 하나씩 보이는 등의 문제가 발생할 수 있다.
하나의 템플릿을 만들었다고 하는데 과연 이 템플릿의 의미가 뭘까? 템플릿은 weight matrix이다. Weight matrix는 학습을 통해 얻어진 parameter(hyperparameter 아님)이다. 따라서, 학습을 진행한다는 것은 결국 weight matrix를 구하겠다는 뜻이다.
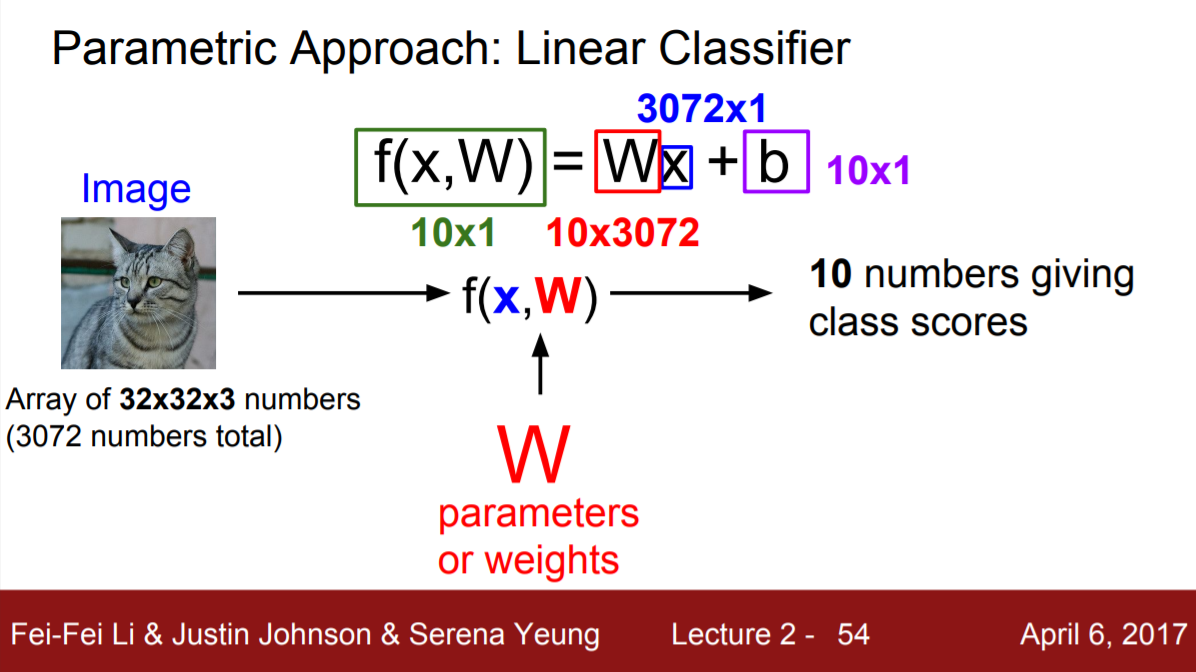
f(x, W) = Wx + b식을 뜯어보자.
- x는 test set에 있는 이미지의 픽셀들을 flatten시킨 입력이다. 이 경우, 32 * 32 크기의 색상 3(r, g, b) 정보를 담고 있기 때문에 3072개의 총 숫자가 존재한다.
- W는 weight matrix로 모델 학습을 통해 얻은 파라미터다. 행렬의 크기는 10 by 3072로 3072 행의 입력정보가 dot product를 해주면 10 by 1 크기의 행렬이 출력된다. 여기서 10은 총 클래스의 수다.
- b는 bias로 클래스 간의 데이터 불균형이 존재할 때 불균형을 완화시킬 때 사용한다. 예를 들어 강아지와 고양이 두 개의 클래스가 존재할 때 고양이의 사진 수가 1000장 있고 강아지의 사진 수가 100장 있을 때 분류기를 통과할 때 고양이 사진을 많이 학습시켰으므로 새로운 사진을 고양이로 분류할 가능성이 커진다. 따라서 적절한 bias를 통해 강아지 클래스에 대한 우선권을 부여해야 한다. 여기서 주목할 점은 bias는 데이터 관련 파라미터로 모델의 학습과는 상관이 없는 변수라는 것이다.
- f(x, W)는 x라는 test set의 이미지와 학습된 W를 통해 얻은 10개의 클래스별 값이다. 여기서의 f는 선형방정식이다.
행렬의 계산과정을 구체적으로 살펴보면 아래와 같다.
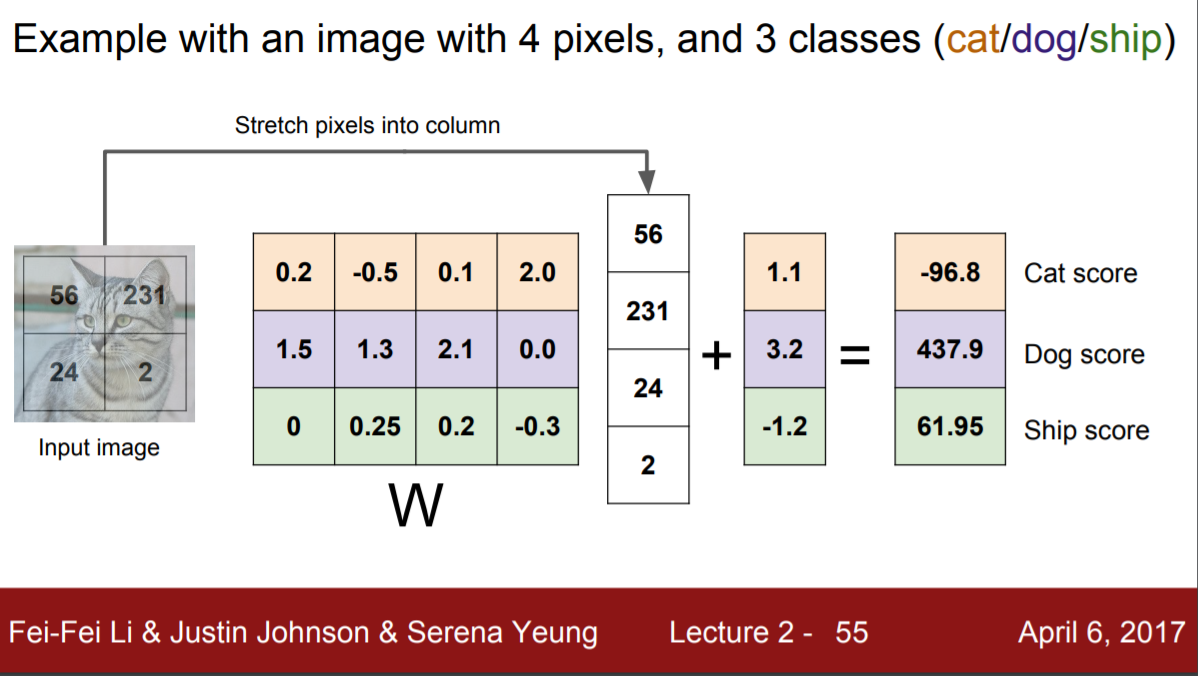
Linear classifier란 말 그대로 선형 분류기인데 고차원 공간에 위치한 이미지를 어떻게 선형적으로 분류한다는 것일까? 시각화를 위해 차원 축소(PCA , NCA,Random Projections와 같은 기법들이 존재한다)해서 선형적으로 분류하면 아래의 슬라이드와 같다. 2차원의 경우 선으로 분류할 수 있고 3차원의 경우 평면으로 분류할 수 있다. 주어진 차원보다 한 차원 낮게 경계점을 그릴 수 있기 때문이다.
참고 : 학습할 때 최적의 W를 찾는 과정에서 2차원으로 표현된 직선의 경우 rotation할 것이고 bias가 바뀌면 직선이 위아래로 이동할 것이다.

이렇게 선형적으로 분류한다면 곡선이 없어서 아래와 같은 decision boundary가 있을 때 분류가 힘들다. 언뜻 보기에도 하나의 직선으로 분홍색과 하늘색을 구분하기 어려운 것을 확인할 수 있다.

추가적으로 사용할 수 있는 방법은 좌표계를 바꿔주는 것이다. 아래의 그림에서 직각좌표계에서 선형으로 분류될 수 없는 datapoint들이 극좌표계로 옮기자 선형 분류가 가능하다는 것을 확인할 수 있다. 하지만 이 방법이 통하는 경우는 드물기 때문에 선형분류기는 한계점이 있다. 따라서, 앞으로 더 복잡한 모양의 분류기에 대해 학습할 것이다.