스탠포드 강의의 CS231n 4강을 보고 정리한 내용입니다.

링크: https://www.youtube.com/watch?v=d14TUNcbn1k&list=PLC1qU-LWwrF64f4QKQT-Vg5Wr4qEE1Zxk&index=4

2강 3강에서는 linear classifier를 주로 다뤘다. 그 과정에서 선형으로 분류할 수 없는 decision boundary가 형성되어있을 때 발생하는 linear classifier의 한계를 지적했다. 그에 대한 해결책으로 비선형 영역을 표현하기 위해 f(W,x) =Wx+b의 선형방정식을 activation function에 통과시킨(비선형성 위해) 퍼셉트론을 여러 layer로 쌓은 신경망이 만들어졌다. 이번 강의부터는 신경망을 공부할 것이다.

지난 강의에서 loss를 최소화하여 최적의 W를 근사적으로 찾아가는 방법인 Optimization에 대해 배웠다. 여기서 말하는 최적의 W를 근사적으로 찾아가는 방법이란 무엇일까? Gradient descent를 통해 weight를 수정해나가는 과정이다.

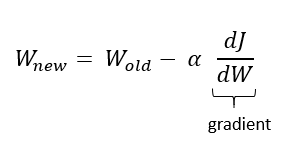
물론 신경망을 이해하고 나서 신경망에서 gradient descent가 어떻게 이루어지는지 보는게 이해가 쉽지만, 본격적으로 신경망을 학습하기 전에 지난 강의와의 연속성 차원에서 backpropogation이 먼저 소개된다. Backpropogation이란 loss function의 gradient를 신경망에서 효율적으로 계산하기 위한 알고리즘이다.

1. Backpropogation

앞서 neural network의 gradient descent를 효율적으로 계산하기 위한 방법이 backpropogation이라고 하였다. Gradient descent를 계산하는 이유는 weight parameter를 수정해가면서 최적의 weight matrix를 구하기 위함이다. Gradient란 loss function을 weight 값에 대해 미분하는 것인데 우선, loss function 식을 다시 한번 보자.

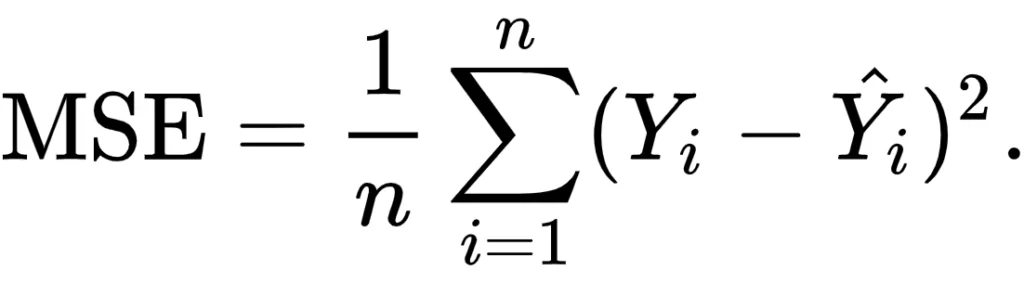
chain rule

위의 loss function 식에서 y값이 정답라벨이고 ŷ(y estimate)이 score function이며 n은 dataset의 수이다. 여기서 loss function[MSE(mean squared error)]을 w로 미분하고자 하는데 w변수가 보이지 않는다. 이게 어떻게 된 일일까? 순방향 신경망의 구조를 보면 이해할 수 있다.

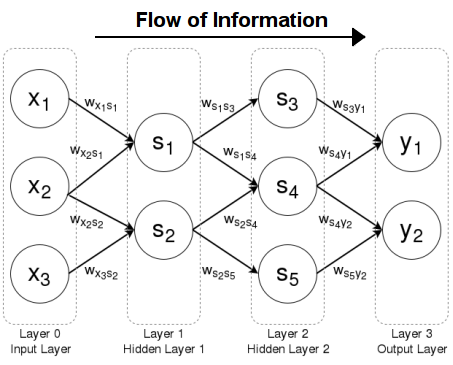
위 그림에서 weight parameter는 output layer의 y1, y2에서 직접적으로 정의되는 것이 아니라 hidden layer의 은닉 뉴런에서 정의된다. 즉, 수학적으로 표현한다면, loss function은 합성 함수이다. 합성함수를 미분할 때 chain rule(연쇄법칙)을 사용한다. 따라서, neural network의 loss function도 chain rule를 사용해서 loss function을 계산해준다.

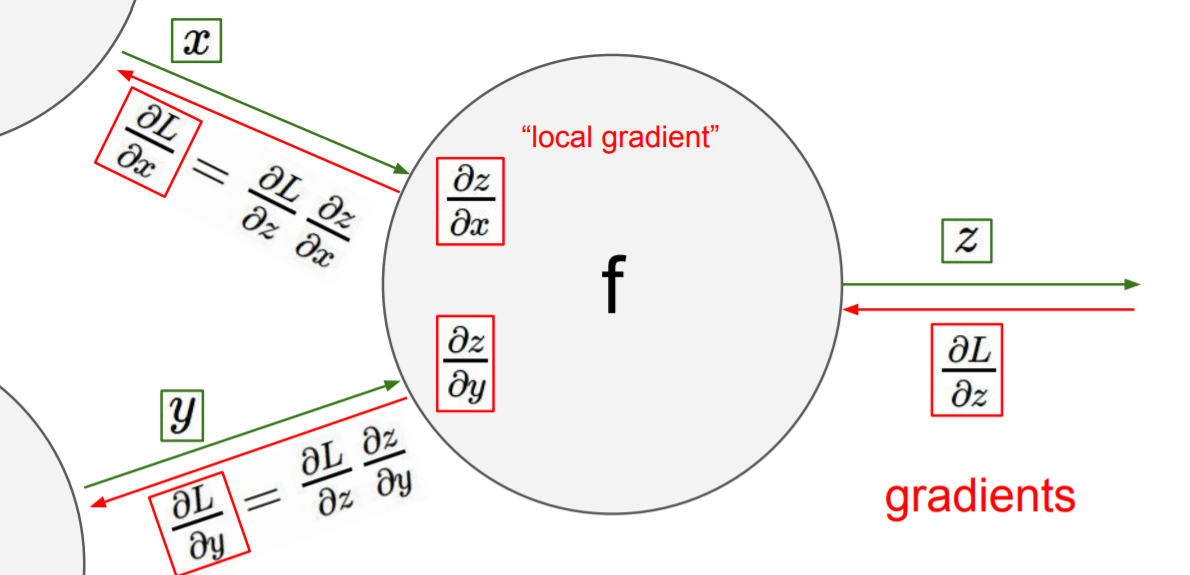
Chain rule은 미분 대상인 함수(L)를 특정 변수(x,y)에 대해 직접적으로 편미분하기 힘들 때, 미분 대상인 함수를 구성하는 직접적인 변수(z)를 매개로 미분을 나눠서 하는 방법이다.

Backpropogation의 효율성

Backpropogation이 chain rule을 사용하는 것까진 파악했는데 어떤 면에서 효율적이라는걸까? Chain rule을 사용한다면 역방향으로 뉴런을 단위로 편미분을 하면서 곱해준다. 뉴런을 단위로 연쇄법칙 미분을 하기 때문에 역방향(output layer(loss function) > input layer)으로 계산할 때 각 뉴런의 미분에 필요한 공통 부분을 저장해놓은 후(forward pass 계산할 때 back propogation시 gradient에 필요한 중간 과정 값들을 저장)각 뉴런에 전달함으로써 미분의 중복을 없애준다. 다시 말해서 weight라는 parameter가 분산된 neural network에서 계산의 중복없는 gradient 계산을 실현해주기 때문에 효율적이다.

위 그림에서 빨간색 박스 친 부분이 output layer로부터 계산된 값으로 upstream gradient이다. 파란색 박스 친 부분이 각 뉴런에서 새로 계산해야 할 부분으로 local gradient이다. Upstream gradient * local gradient = total gradient로, 계산의 중복을 피할 수 있는 것을 수식으로도 확인했다.

Backpropogation의 의미(신경망)

Backpropogation 알고리즘은 전체 구조를 알지 않아도 각 뉴런에서 local하게 미분을 함으로써 서로 소통한다는 점에서 뇌의 신경망과 비슷하다. 다시 말해서, 각 뉴런 입장에선 주위만 둘러보면 되지만, 여러 뉴런들이 상호작용하면서 weight(시냅스의 연결 강도)가 조절된다.

Computational Graph(뉴런 단위)

신경망은 input layer, 여러 개의 hidden layer와 output layer, 또 각 layer는 여러 개의 뉴런으로 이루어진 아주 복잡한 구조로 이루어져있다. 그래서 변수가 너무 많고 복잡한 함수의 경우 미분을 하는 것이 어렵다. 이 때 gradient 계산을 쉽게 하기 위해 미분 과정을 쪼개서 시각화하는 것이 computational graph다. CS231n강의는 여기서부터 본격적으로 시작한다.

Tradeoff(math vs simple graph)

Tradeoff의 중요성은 앞의 블로그에서도 강조했다. Computational graph가 시각적으로 간단하기 위해선 미분이 복잡해질 것이고 computational graph가 복잡해지면 local하게 계산해야하는 미분식이 간단해질 것이다.

예시 1

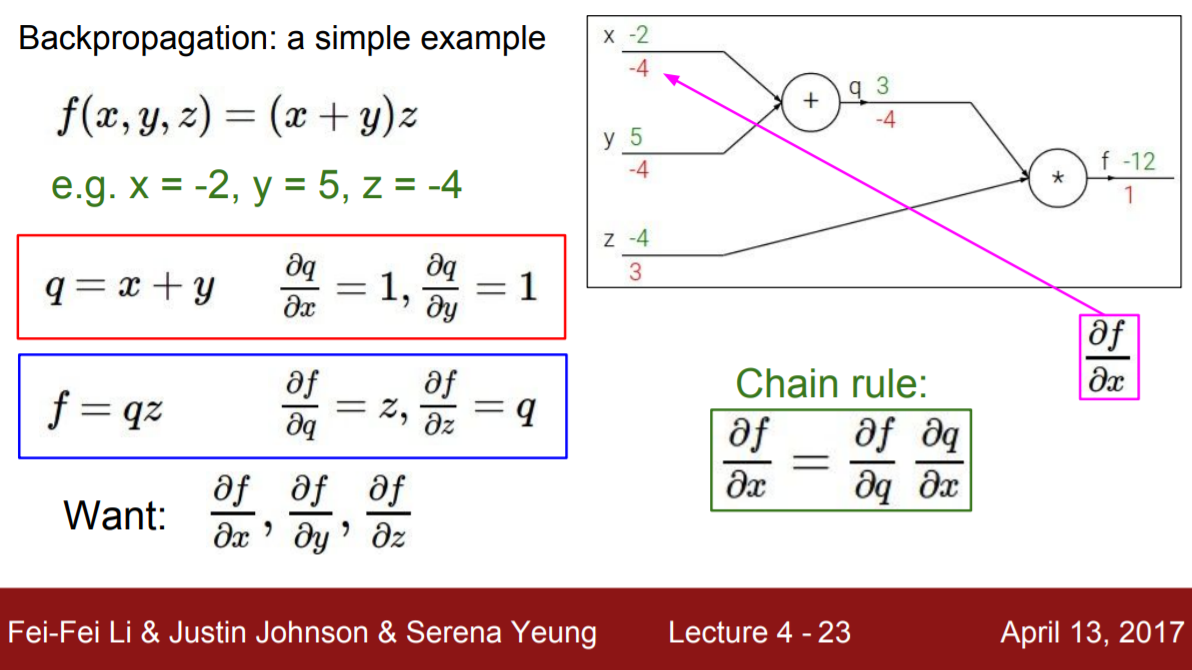
Forward pass

Forward pass의 값들을 순차적으로 계산하면 f값을 최종적으로 구할 수 있다. 또한 각 뉴런에 중간값들을 저장해놔서 backpropogation 계산 시 이용하도록 한다. 중간값들은 위의 그래프에서 초록색으로 표시된 값들이다.

Backpropogation

위 그림에서 Backpropogation은 빨간색으로 표시됐다. Chain rule을 통한 과정을 보면,
조건: x = -2, y = 5, z = -4, f = qz, q = x + y일때,
1. f에 대한 local gradient 계산:

• σf/σq = z(-4)
• σf/σz = q(3(forward pass로 x(-2)+y(5)=3이 저장됨))

2. q에 대한 local gradient 계산:

• σq/σx = 1
• σq/σy = 1
  이 때, f에 대한 local gradient σf/σq = z(-4)는 upstream gradient가 된다.

3. 최종적으로 구하고자하는 gradient = upstream gradient x local gradient로

• σf/σx = σf/σq(-4) * σq/σx(1) = -4
• σf/σy = σf/σq(-4) * σq/σy(1) = -4
• σf/σz = 3

예시 2

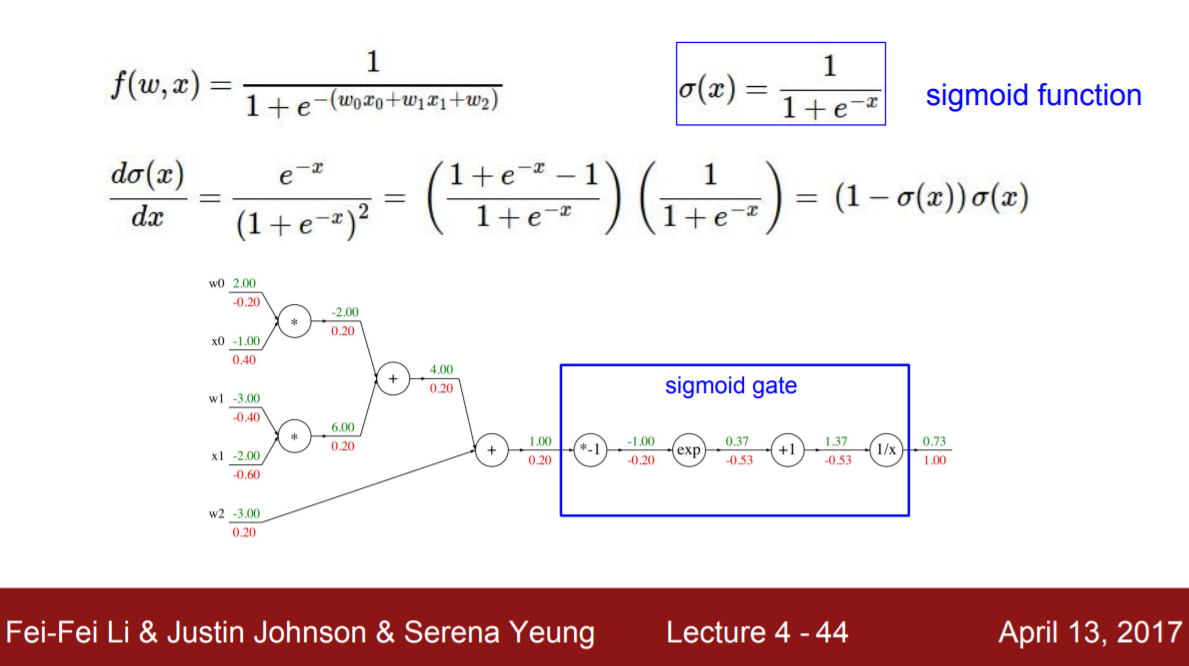
Weight와 x값을 더한 score function을 활성화 함수 중 하나인 sigmoid에 통과시킨 예시가 강의에 설명되었다. 예시 1과 같은 계산을 혼자서 해보면서 연습하자. 여기서 편미분이 쓰였으니 이 과정을 이해하려면 편미분 개념을 공부해보자. 위에서 편미분을 할 때 필요한 식들은 아래에 있다.

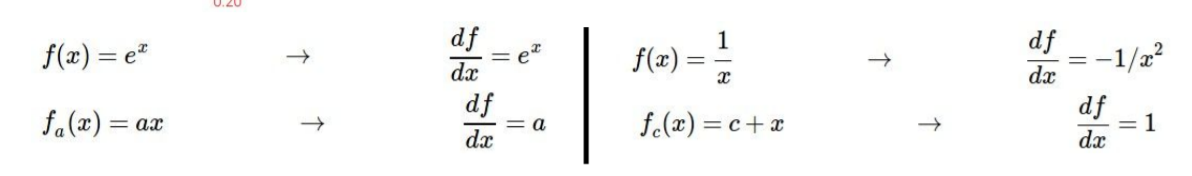
자세한 계산 과정은 https://softwareeng.tistory.com/entry/cs231n-4%EA%B0%95-%EC%97%AD%EC%A0%84%ED%8C%8C%EC%99%80-%EC%8B%A0%EA%B2%BD%EB%A7%9D-24-%EC%97%AD%EC%A0%84%ED%8C%8C-%EC%8B%AC%ED%99%94-backprobagation 여기를 참고하자.

흔히 쓰이는 노드(gate)

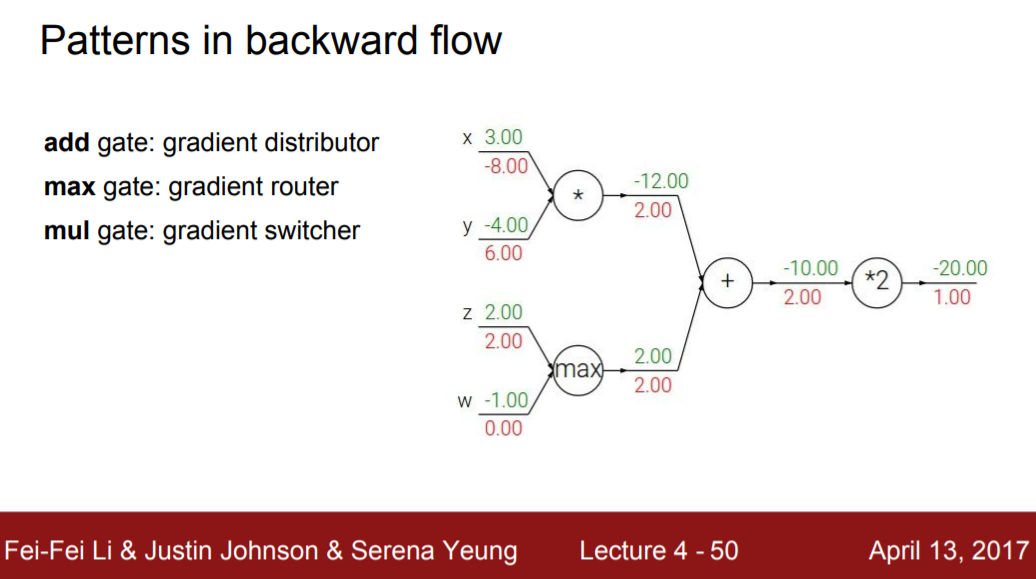
이 부분에 대한 설명은 https://blog.naver.com/riverrun17/221900860949 에서 가져왔습니다.

1. Add gate(gradient distributer)

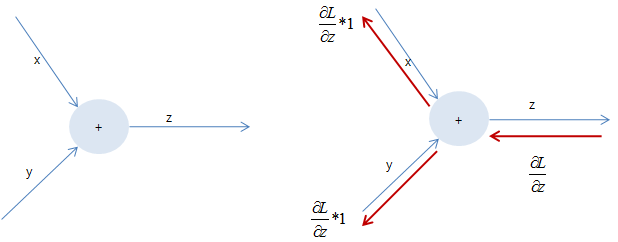
z = x + y의 local gradient는 σz/σx = 1, σz/σy = 1이니까 total gradient는 upstream gradient와 같다.

2. Max gate(gradient router)

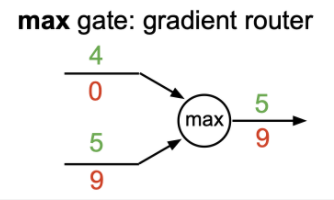
z = max(x, y)의 local gradient는

• x >= y 일 때 σz/σx = 1, σz/σy = 0
• x <= y 일 때 σz/σx = 0, σz/σy = 1
  으로 더 큰 값의 노드에 upstream gradient * 1로 gradient 값이 route되고 작은 값의 노드는 0이다.

3. Mul gate(swap multiplier)

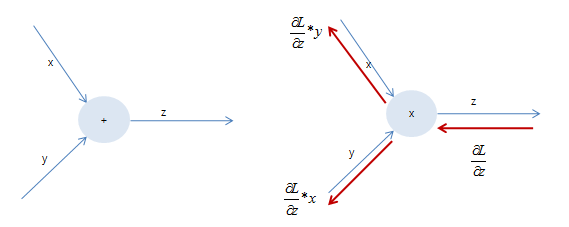
z = x * y의 local gradient는 σz/σx = y, σz/σy = x니까 upstream gradient와 곱해지는 local gradient는 상대방 노드에 저장된 값이다.

Computational Graph(계층 단위)

예시 1에선 기본적인 식 (x+y)z 의 backpropogation, 예시 2에선 sigmoid 함수를 통과한 w * x의 값(뉴런 단위)의 backpropogation 과정을 보여줬다. 이번에는 여러 개의 뉴런이 모인 계층 단위에서의 backpropogation을 보여줄 것이다.

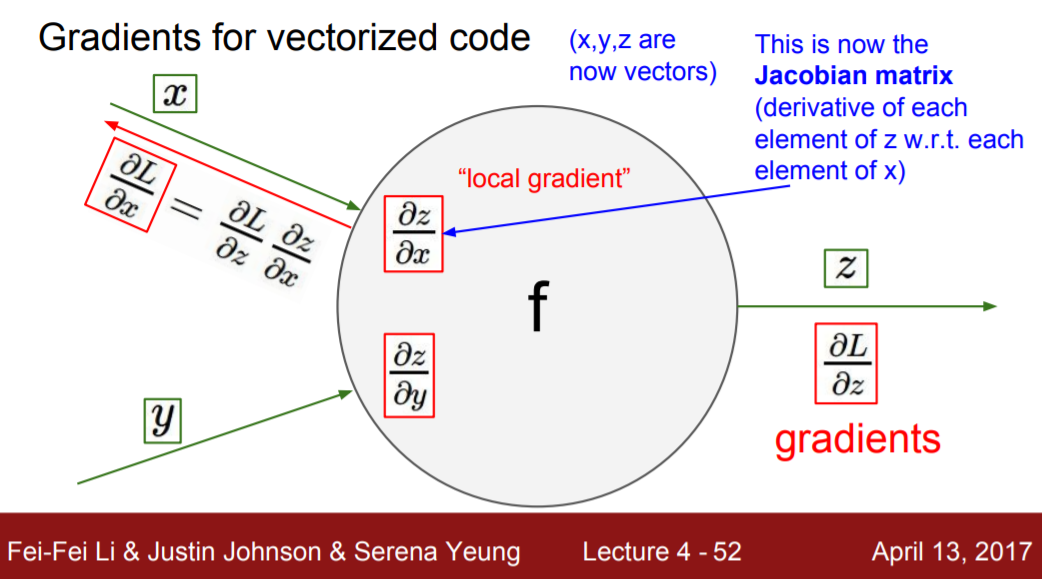
전에는 뉴런의 값이 입력되어 x1, x2..가 스칼라였다. f(x1, x2,...)는 변수 n차원 벡터이고 함수값이 스칼라일 때, 함수 f(x1,x2,...)를 σf/σx1, σf/σx2..처럼 각 요소별로 편미분한 벡터가 gradient다.



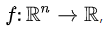
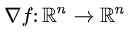
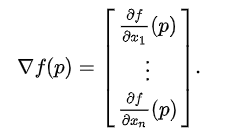
하지만 layer 단위로 입력되게 되면 layer에 여러 개의 뉴런이 입력되기 때문에 x1, x2...가 vector다. 이 때, f(x1,x2,...xn)이 n차원 벡터이고 함수 값이 m차원 벡터일 때, 함수 f 벡터의 요소들을 x벡터의 요소별로 편미분하면 mxn matric 형태의 jacobian matrix가 된다.

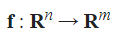
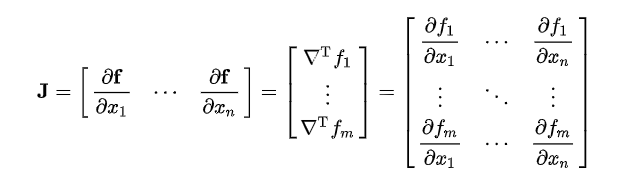
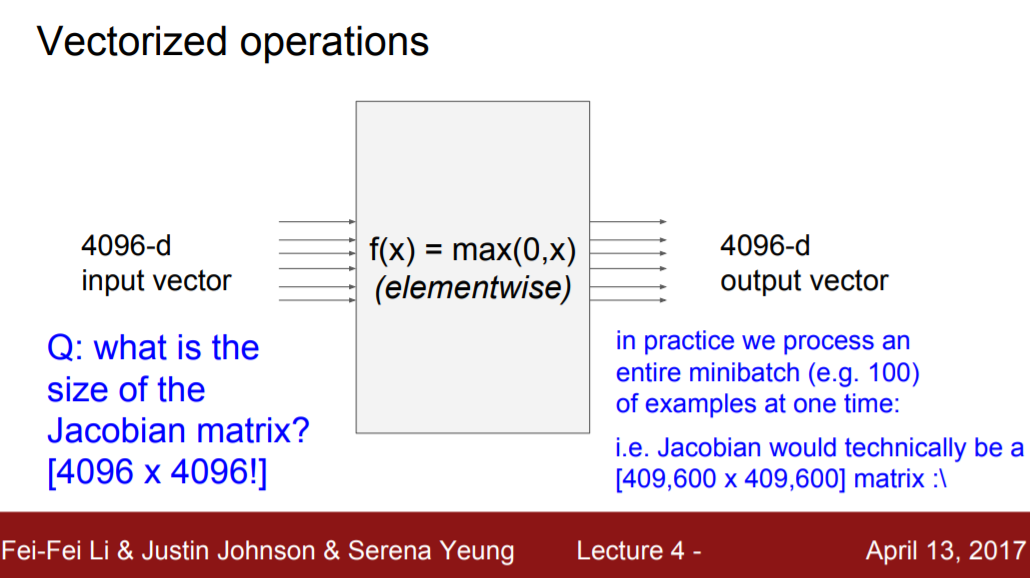
예시 3

마지막으로 강의에서 든 예시는 벡터 미분 과정을 보여준다. 앞에서 배운 과정을 행렬 미분을 통해 적용해보자. 혼자서 계산해보고 자세한 식 풀이과정은 https://softwareeng.tistory.com/entry/cs231n-4%EA%B0%95-%EC%97%AD%EC%A0%84%ED%8C%8C%EC%99%80-%EC%8B%A0%EA%B2%BD%EB%A7%9D-35-%EC%97%AD%EC%A0%84%ED%8C%8C-%ED%8C%A8%ED%84%B4%EA%B3%BC-%EB%B2%A1%ED%84%B0-backpropagation-pattern-and-vector 여기를 참고하자.

모듈화된 API

각 노드 별로 forward pass랑 backard propogation 수식이 정리된 API가 제공되므로 실질적으로는 backpropogation을 수학적으로 계산할 일이 실제로는 별로 없을 듯하다.

2. Neural Network

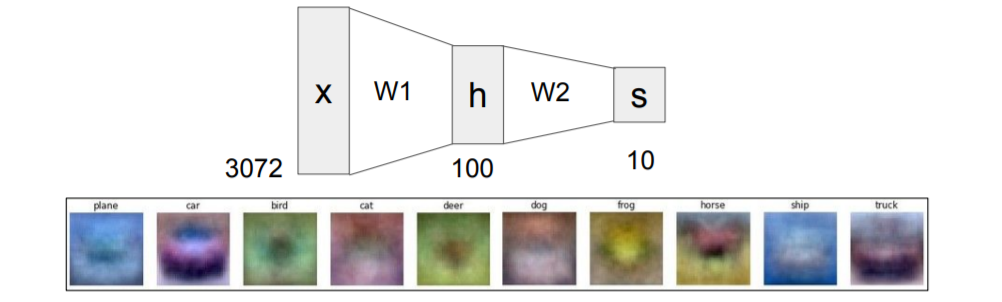
앞서 linear classifier에선 하나의 template을 통해 각 카테고리를 표현해주기 때문에 차의 비유에선 빨간차 외의 다른 색깔의 차를 표현해줄 수 없다는 문제가 있었다. 하지만 neural network의 경우에는 여러 색깔의 차 중에서 weight를 학습하므로 다양한 색깔의 차를 제대로 분류할 수 있게 된다.

Neural network란 간단한 함수들을 쌓아서 복잡한 non-linear function을 표현하고자 한다. 이 때 주의할 점은 만약 선형함수에 선형함수를 통과한다면 선형함수가 나오게되어 층을 여러 개 쌓는 것이 의미 없어진다는 것이다. (엄밀히 말하면 선형함수는 0 input vector에 대해 0 vector가 출력되어야해서 f(x) = ax + b는 affine하다.)수학적으로 표현하자면 f(x) = ax + b, g(x) = cx + d가 있을 때 f(g(x)) = a(cx+d)+b = (ac)x + (ad + b) 의 선형함수가 나온다. 따라서 fully-connected layer들 사이에 activation function(비선형성)을 통해 neural network에 비선형성을 부여해준다.

Activation function

Activation function들은 위에서 보이듯이 비선형적이며 주로 ReLU함수를 많이 쓴다. 그 이유에 대해서는 6강에 자세히 나와있다.