AMSgrad 논문 정리

On the convergence of ADAM and BEYOND

저자 : Sashank J.Reddi, Satyen Kale&Sanjiv Kumar

링크 : https://arxiv.org/abs/1904.09237

1. 기존 알고리즘과의 차이(ADAM 알고리즘과의 비교)

엔지니어링은 문제점에 대한 해결책을 끊임없이 제시하는 과정이다. Optimizer algorithm 역시 각 알고리즘에 대한 문제점을 해결하는 방향으로 알고리즘들이 수정되고 있다.

SGD(stochastic gradient descent)는 local minimum에 도달했을 때 빠져나올 수 없고, learning rate가 일정해서 minima에서 oscillate한다는 문제점이 있다. 그에 대한 해결책으로 local minimum에서 빠져나오기 위해 RMS prop은 momentum이라는 개념을 도입했다. 또한 Oscillating problem을 해결하기 위해 learning rate를 변수로 하는 Adadelta 알고리즘이 만들어졌다. 이러한 두 해결책을 취합한 알고리즘이 ADAM 알고리즘이다. 즉, ADAM 알고리즘은 1st momentum과 2nd momentum을 사용하고 adaptive learning rate를 사용한다.

ADAgrad는 gradient가 작거나 멀리 떨어져 있을 때 성능이 좋으나, gradient가 크거나 고밀도일 때, 즉 고차원 모델을 optimize할때 급격하게 성능이 떨어진다. 그 이유는 learning rate가 averaging past gradient의 루트를 사용하기 떄문이다. 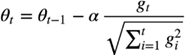과거의 gradient가 크거나 gradient들이 연속적으로 몰려있을 때 learning rate의 분모항이 급격히 커져 위식에서 step size가 0으로 수렴한다. 그 결과 loss 값이 줄어들지 않고 정지해 학습이 더 이상 불가능해진다.

ADAM은 learning rate의 급격한 감소를 막기 위해 원인이 되는 averaging past gradient의 루트 식을 변형해주었다. Exponential moving average of squared past gradient를 대신 사용해주었는데 squared past gradients의 중심축을 이동시킨다는 뜻이다.

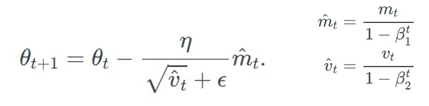
중심축을 이동시키면 과거 전체의 gradient를 모두 감안해 learning rate를 바꾸는 대신 직전 몇개의 gradient만을 참고해서 learning rate를 업데이트하게 된다. 안타깝게도 직전 몇 개의 항만을 고려하는 것이 convergence issue를 일으켰다. Convergence를 위한 필요조건은 gradient들의 장기 기억이기 때문이다. Stochastic minibatch 중 방향을 찾는데 중요한 gradient들이 분명히 존재한다. 하지만 exponential averaging에 의해 이 gradient 들의 영향이 사라지기 때문에 장기기억이 없다.

AMSgrad는 convergence의 필요조건인 장기기억을 ADAM과 달리 구현해 convergence에 한 걸음 더 가까워지고자 한다.

2. 알고리즘의 기본원리 및 아이디어

AMSgrad는 수렴의 필요조건인 장기기억의 보존을 가능하게 하는 방향으로 식을 수정하였다. ADAM optimizer 기존의 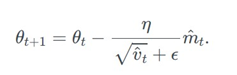식에서 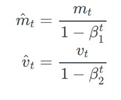Exponential moving average of squared past gradient를 사용하는 대신 과거에서부터 현재까지의 vt 중 가장 큰 vt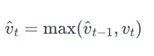를 사용함으로써 과거의 정보를 보존하였다. 따라서, Stochastic minibatch 중 방향을 찾는데 중요한 큰gradient의 정보를 계속 가지고 있는 것이 가능해졌다. 또한, v-hat는 항상 max 값만을 취하기 때문에 감소하지 않아 step size는 증가하지 않는다.

이제, 장기기억의 보존이 왜 수렴의 필요조건인지 식으로 설명해보고자 한다.

ADAM논문에서 convergence를 증명했지만 증명의 결과가 거짓인 이유는 AMSgrad 논문 의 저자에 의하면 가정이 잘못되었기 때문이라고 한다. ADAM 논문의 저자는 learning rate의 변화에 반비례하는 감마
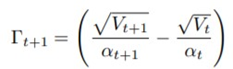라는 상수를 정의했으며, 감마가 0 이상이라고 가정을 했었다. 감마가 0 이상이기 위해서는 learning rate가 증가해서는 안되는 것을 식에서 알 수 있다.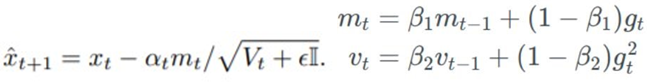

Learning rate는 증가하면 안되므로 분모가 분자보다 큰 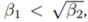라는 조건이 성립해야 한다. 베 타1과 베타2의 루트는 gradient에 따라 learning rate에 동일한 비중의 영향을 끼치기 때문이다.(베 타2는 gradient의 제곱이 곱해졌지만 루트가 씌어지기 때문에 gt에 의한 영향이 비슷해질 것이다) 하지만 분모는 0이 될 수 없으므로 항상 0보다 큰 epsilon이 생기면서 시간과 비례하게 분모 값 이 더 커진다. 따라서 시간에 따라 베타1의 값은 감소하고 베타2의 값이 증가해야한다는 조건이 추가적으로 충족되어야 한다. 정리하면, ADAM 논문은 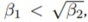을 만족하는 베타1과 베타2를 상 수로 가정했기 때문에 감마가 0이상이라고 짐작한 점이 틀렸다. 감마가 0이상으로 시작해도 시간 이 지나면 0이하가 될 가능성이 있기 때문이다.

AMSgrad는 베타2가 상수일지라도 step size가 증가하지 않게하는 방법을 제안했다. 여 기서 베타2가 베타1에 비해 큰 값이어서 critical하므로 베타2를 기준으로 생각했다. 기존의 알고 리즘들은 learning rate를 time dependant하게 adapt 시켜 step size가 감소하지 않도록 시도했다. 하지만 Learning rate를 시간에 따라 증가하도록 adapt하건 시간에 따라 감소하도록 adapt하건 각 자 성능을 악화시킨다는 것을 보고서 시작할 때 확인하였다. 따라서, Adagrad는 learning rate를 adapt 시키는 대신 v(t)를 adapt 시키는 방향으로 생각을 전환했다. 이 아이디어가 논문의 핵심인 것 같다. 현재 v(t)값보다 클 정도로 gradient가 급격하게 증가하는 상황에서 V(t)는 새롭게 증가 한 gradient가 되어 그 정보를 보존한다. 이렇게 되면 step size는 감소만해서 learning rate가 시간 에 따라 감소할 때랑 비슷한 문제가 발생한다. Learning이 정체되는 것이다. 만약 v(t)를 아주 천천 히 감소시킨다면 learning rate가 천천히 증가해 learning의 정체를 막지만 gradient의 정보도 영원 히 보존되지 않는다. 다만 핵심은 v(t)를 아주 ‘천천히’ 감소시켜 중요한 gradient의 정보를 영원히 는 아니지만 장기간 보존할 수 있게 된다는 것이다. 즉, V(t)를 변화시켜 learning rate가 증가 혹은 감소 한 방향으로만 진행되는 것이 아니라 왔다 갔다 하도록 했다.

3. Convergence guarantee 여부

결론부터 말하면 Convergence guarantee는 ADAM optimizer의 convergence guarantee가 성립하지 않았던 이유와 같은 이유로 없다.

우선, v(t)를 감소시킴으로써 비록 정도는 미미하지만 step size가 증가하게 되는 구간이 생긴다. 따라서,
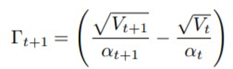의 감마가 음수일 때가 생긴다.

Regret이란 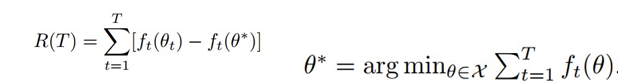으로 step t에서 세타와 세타스타의 차이를 측정하는 것이다. Regret이 상수에 bound되어 있다면 convergence가 성립한다. 하지만 ADAM optimizer 논문에서 R(T)가 논문의 저자는 R(T)가 상수 * (루트 T) 만 되어도 양변을 T로 나누어 무한대로 보내면 0으로 수렴하기 때문에 충분하다고 했다. 하지만 이 가정이 틀렸기 때문에 convergence가 성립하지 않았었다.

AMSgrad의 Regret은 몇 개의 가정을 거친 후 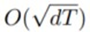보다 작다는 것을 확인할 수 있다. 추가적으로 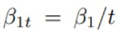와 같이 베타1이 감소하더라도 RT는 최악의 경우에도 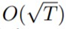에 의해 bound 된다. Regret의 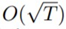에 의해 bound되는 특성으로부터 convergance를 증명하지만, ADAM의 경우와 마찬가지로 convergence가 guarantee되지 않는다.

1)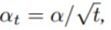 : 시간에 따라 감소하는 learning rate
2)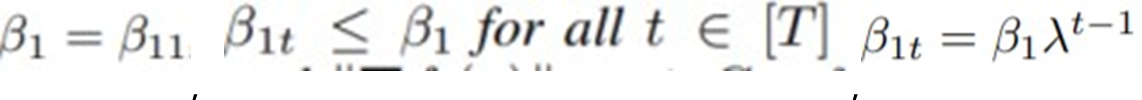: 베타가 행렬이어서 생기는 여러 가정들
3)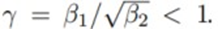 : Learning rate가 증가하지 않도록 하는 가정(앞에서 설명)
4)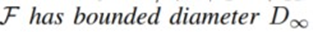: F라는 subspace에 projection 해서 생각, 미지수보다 방정식
이 많은 해가 존재하지 않는 case(overdetermined case)이므로 projection 시켜서 가장 근접한 해 x hat을 구하고자 하는 시도, F가 유한한 평면이다
5)
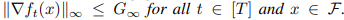
는 gradient의 stochastic한 version, 즉 batch를 뽑을 때마다 임의로 다른 원소들을 뽑기 때문에 확률의 영향을 받는다는 뜻, stochastic하게 뽑은 batch의 gradient가 무한대로 크게 움직이지 않는다는 뜻
6)
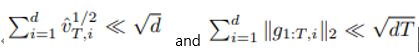
: RT의 첫 번째 항과 3번째 항이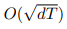
보다 작다는 것을 나타내기 위함, 두 번째 항은 상수

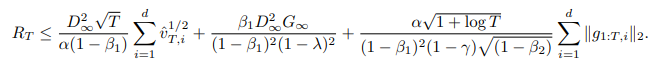
Convergence가 완전히 보장된다면 어떨까 잠시 생각을 해보았다. Convergence가 완전 히 보장된다면 local minima가 아무리 얕아도 converge해버리는 것은 아닌가 의문이 들었다. loss 함수의 전체적인 모양을 알 수 없으므로 local minima와 global minima를 구분하는 것은 사실상 불가능한데 만약 convergence가 보장된다면 얕은 local minima에서도 converge해버려서 빠져나올 수 없게 되는 것인지 궁금하다. 만약 그렇다면 convergence가 보장되는 것이 꼭 좋은 것인지 의문이다.

4. 시뮬레이션/ 실험

각자 convex한 경우(multiclass classification using logistic regression)와 nonconvex(neural networks)한 경우의 시뮬레이션 결과가 있었다. 그 중 Synthetic한 경우의 시뮬레이션을 통해 개 념을 적용해볼 것이다.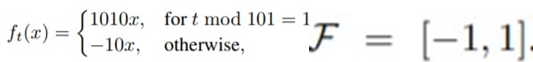

(one-dimensional convex)

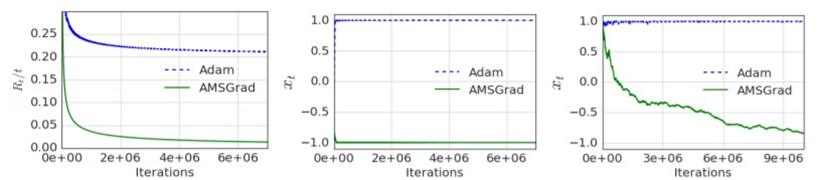
Mod 101은 100번 gradient -10을 얻을 때 1번 gradient 1010을 얻는다는 뜻이다. Gradient가 -10 일 때는 양의 방향(Loss가 커지는 방향) 으로 공이 진행하게 되고(비유) 1010일 때 음의 방향(Loss 가 감소하는 방향)으로 진행한다. 따라서 더 큰 음수 값일수록 converge하는 방향으로 이동했다 고 할 수 있으며, 반대로 더 큰 양수 값일수록 converge하지 않고 엉뚱한 방향으로 이동했다고 할 수 있다. 범위가 +∞부터 -∞까지 진행될 수 있으므로 -1부터 1까지 범위가 한정되는 1차함수 인 F 함수에 값을 projection시킨다. 따라서 -1에 가까울 수록 minimum regret을 가지고 converge 하며 반대로 +1에 가까워질수록 convergence와는 거리가 멀어진다. 표에서 Adam은 x가 1에 근 접하는 반면에 AMSGrad는 -1에 근접해 average regret이 0에 근접하므로 이 특정한 가상 상황에 서는 Adam은 converge하지 않는 반면 AMSGrad는 converge한다는 것을 실험으로 보일 수 있다. AMSgrad는 장기기억력이 있으므로 1010만큼 음의 방향의 gradient가 101번 중 한번 나왔더라도 나머지 100번 이동할 때도 영향을 줘서 이러한 결과가 나왔을 것이다. 하지만 이 경우로 현실에 완벽하게 적용 가능하다고 보기 힘든게 공의 비유에서 공이 101번 굴렀다고 했을 때 100 번을 올라가는 경우를 상상하기 힘들기 때문이다. 현실성이 없는 가정이라고 생각했다.