학습 기법

시대를 초월하는 모델링 학습

우리가 관심있는 모델은 특정한 범위에 한정된 작업을 수행하기 위해 만들어진 모델이 아닌 입출력 쌍을 활용한 다양한 유사 작업에 대해 스스로를 최적화하기 위해 자동으로 적응하는 모델이다. 파이토치는 파라미터 관점에서 잔차(fitting error)의 미분을 분석적으로 표현하기 위한 모델을 쉽게 생성하도록 설계되어 있다.

이 장에서는 일반 함수의 적합(fitting)을 자동화 하는 방법에 대해 다룬다. 심층 신경망은 일반 함수이며, 파이토치는 심층신경망의 적합을 자동화하는 과정을 최대한 단순하고 투명하게 만들어준다.

학습은 파라미터 추정에 불과

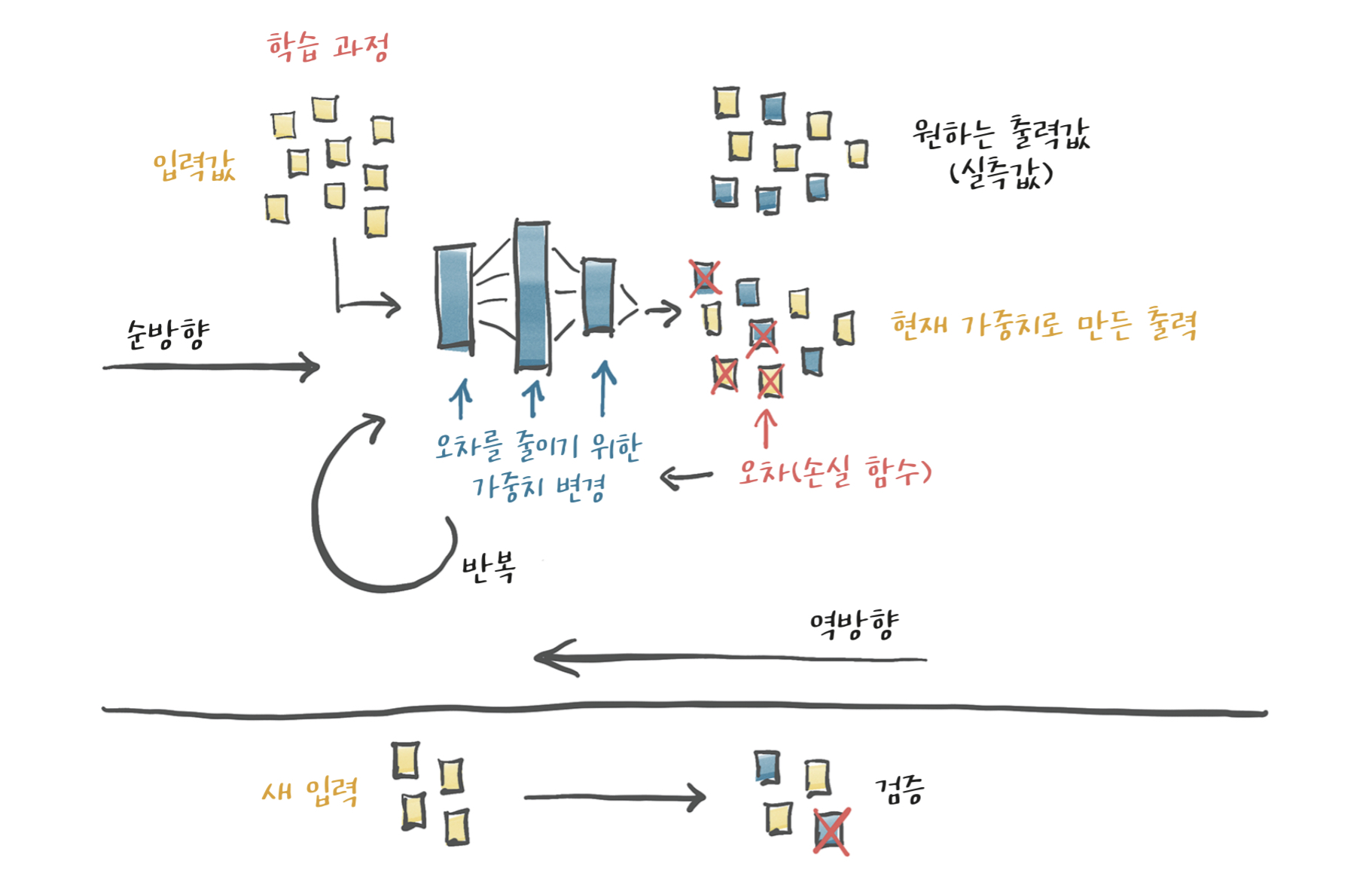
입력 및 입력에 대응하는 출력인 실측자료(truth 값)와 가중치 초깃값이 주어졌을 때, 모델에 입력 데이터가 들어가고(순방향 전달) 실측값과 출력 결괏값을 비교해서 오차를 계산한다. 그리고 모델의 파라미터(가중치)를 최적화하기 위해 가중치를 오차값에 따라 일정 단위(학습률)만큼 변경한다. 이 변경된 값은 합성 함수의 미분값을 연속으로 계산하는 chain rule을 통해 정해진다. 이 과정은 출력값과 실측값과의 오류, 즉 값의 차이가 일정 수준 이하로 떨어질 때까지 반복된다.

온도문제

아날로그 온도계를 구매했다고 가정하고, 온도계를 읽어 온도를 기록한 데이터셋을 만든 후 학습을 위한 모델을 하나 골라 오차가 충분히 낮아질 때까지 반복적으로 가중치를 조절해서 마지막에는 우리가 이해하는 온도 단위로 새로운 눈금을 해석할 수 있도록 해보자.

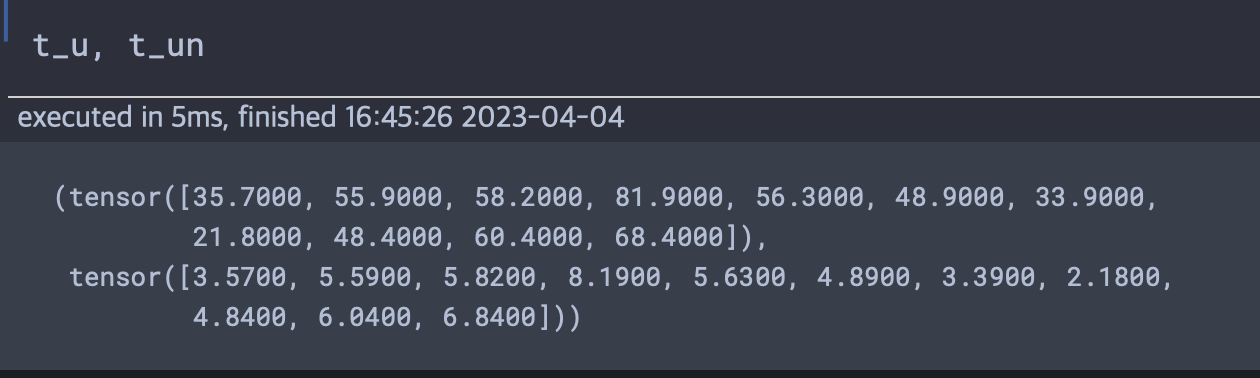
t_c = [0.5,  14.0, 15.0, 28.0, 11.0,  8.0,  3.0, -4.0,  6.0, 13.0, 21.0]
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]
t_c = torch.tensor(t_c)
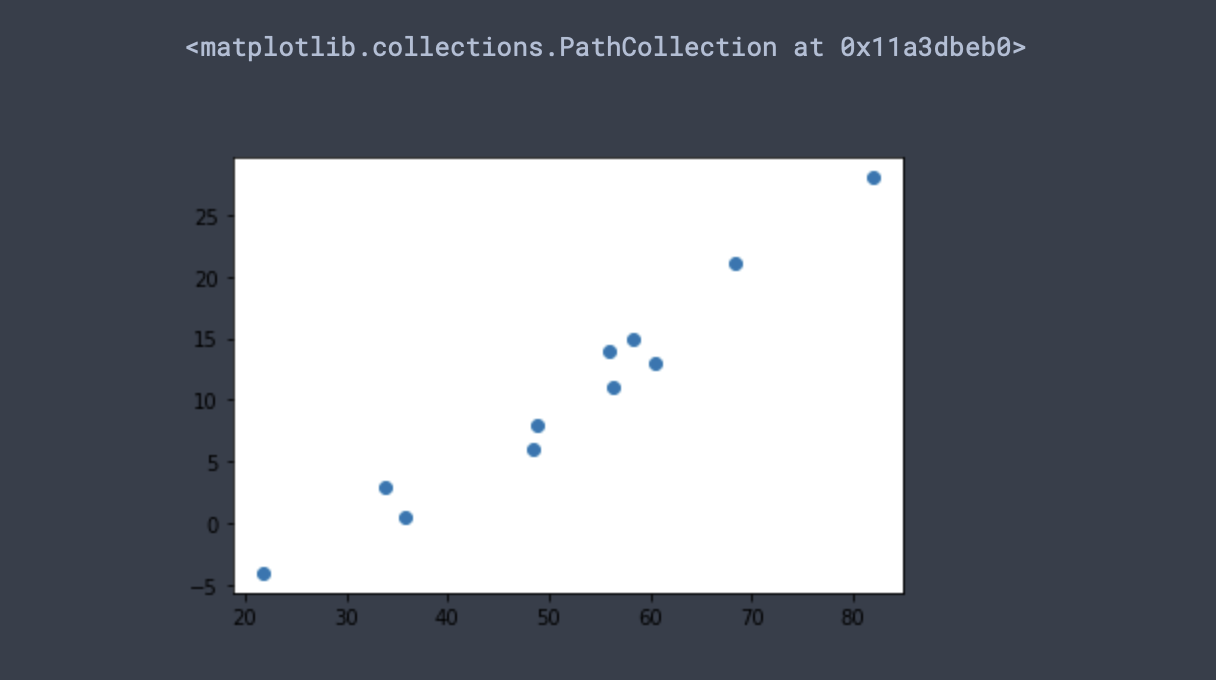
t_u = torch.tensor(t_u)

t_c값은 섭씨 온도 값이며 t_u는 우리가 모르는 단위의 값이다. 데이터를 시각화해보면 노이즈가 있지만 일정한 패턴을 확인할 수 있다.

먼저 선형모델을 골라 시도해보기

답을 모른다고 가정하고 t_c = w x t_u + b로 하여금 선형 관계를 먼저 테스트 해보도록 한다. 가중치와 편향값을 각각 w와 b로 부르자. 앞으로도 계속 보일 표현이니 기억하도록 하자.

이제 파라미터 w, b를 데이터 기반으로 추정해야 한다. 이렇게 함으로써 모델을 통해 t_u로 표기한 알 수 없는 온도값을 섭씨 단위로 측정한 실측 값에 최대한 가깝도록 만들게 된다. 오차 측정 어떻게 할 지 구체적으로 정의해야 하는데, 손실함수(loss function)라 불리는 측정함수를 만들어 오차가 높으면 손실함수도 높은 값을 출력하도록 하면 된다.

손실 줄이기

우리의 경우에서 손실 함수는 모델이 출력한 온도인 t_p와 계측한 값과의 차이인 t_p - t_c이다. 여기서 손실함수는 항상 양수의 차이가 나오게 해야하기 때문에 abs(t_p - t_c) 또는 (t_p - t_c)^2를 사용할 수 있다. 우리는 이중 후자의 경우를 사용한다. 직접 그래프를 그려보면 후자의 그래프가 미분값을 정의할 수 있기 때문이다.

# 모델 제작 및 손실함수 제작 (선형관점)
def model(t_u, w, b):
    return w * t_u + b
def loss_fn(t_p, t_c):
    squared_diffs = (t_p - t_c)**2
    return squared_diffs.mean()

브로드캐스팅(broadcasting)
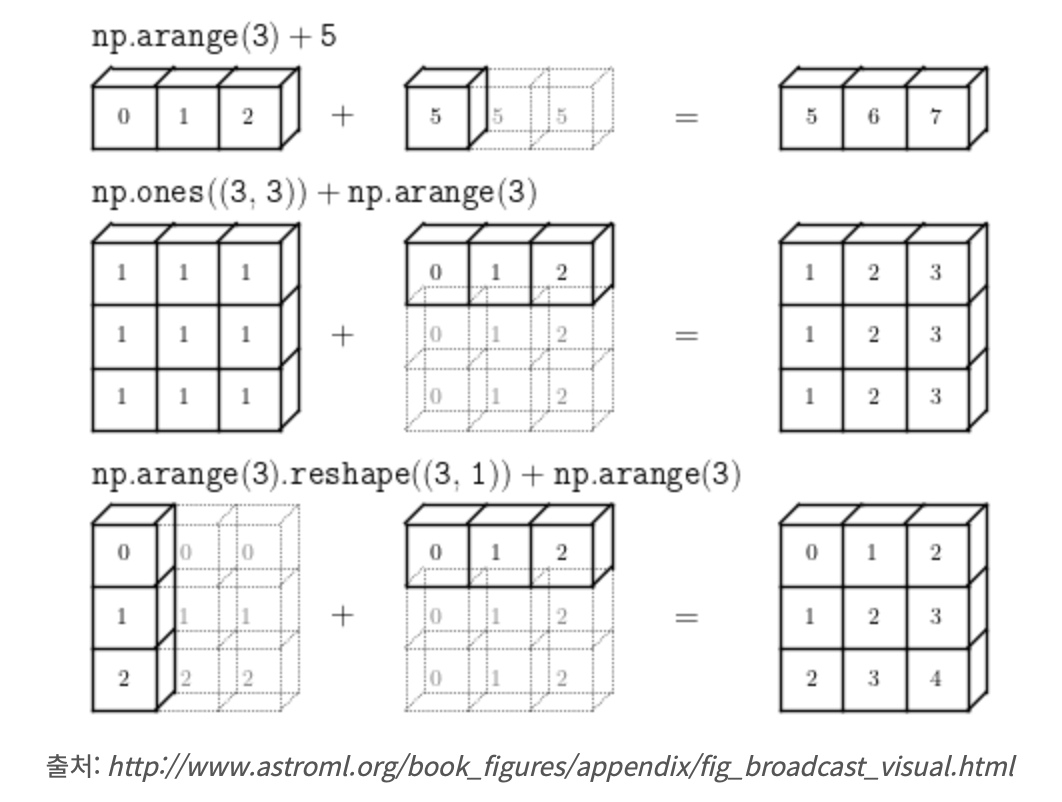
넘파이의 잘 알려진 기능 중 하나인 브로드캐스팅은 파이토치에도 반영되었으며, 대부분의 이항 연산에 대해 제약을 해소해준다. 아래 그림을 참고하면 이해가 쉽다. 첫번째 경우는 1x3배열에 1x1 배열을 더하는 것이다. 자동적으로 1x3모양에 맞추어 1x1요소가 그대로 복사되어 1x3을 형성하고 서로 더해진다.(곱셈도 동일, 점곱과는 다름), 세번째 경우는 3x1 과 1x3의 조합이다. 서로 더해지기 위해서는 각자가 3x3이 되어야한다. 둘다 0,1,2의 숫자를 지니지만 복사되고 나서인 3x3배열에서의 형태는 서로가 다르게 형성되어 더해진다.

경사를 따라 내려가기

이제 경사하강(gradient descent)알고리즘을 통해 파라미터 관점에서 손실함수를 최적화한다. 즉 손실함수의 최솟값 지점을 찾는 것이다. 손실함수의 최솟값 지점을 찾는 과정은 굉장히 상식적이면서 귀납적이다. 우리는 w와 b의 변화정도가 손실에 어느정도 변화를 가져올지 처음에는 알지 못한다. 하지만 w, b의 임의적 변화를 통해 그에 대한 감을 얻을 수 있고, 손실이 현재 매우 큰 상태라면 방향만 결정되었다면 w,b를 크게 움직여서 일단은 손실을 큰 보폭으로 줄여나간다. 그러다가 손실이 줄어드는 것이 아닌 다시 커질때 우리는 현재 변화와 이전 변화 사이에 최솟값을 보이는 w,b가 있다는 것을 알 수 있다. 그러므로 그 시점부터는 w,b의 변화를 천천히 가져가면서 최솟값에 수렴하도록 유도한다. 이것이 경사하강법의 원리이다.

손실 줄이기

위에서 쓰여진 시나리오로 하여금 직접 코딩을 통해 알아보도록 한다.

def model(t_u, w, b):
    return w * t_u + b
def loss_fn(t_p, t_c):
    squared_diffs = (t_p - t_c)**2
    return squared_diffs.mean()

w = torch.ones(())
b = torch.zeros(())

delta = 0.1

loss_rate_of_change_w = \
    (loss_fn(model(t_u, w + delta, b),t_c)) - 
    (loss_fn(model(t_u, w - delta, b),t_c)) / (2.0 * delta)

이 코드는 현재의 w, b값에서 특정단위만큼 w가 증가했을 때의 손실이 변하게 되는데, 값이 줄어들면 w를 더 늘려서 손실을 최소화하고, 값이 줄어들면 w를 늘려서 손실을 최소화한다. 그렇다면 w의 변화를 어떻게 주어야할까? 이것은 손실의 변화 비율에 비례하여 w를 바꾸는 편이 좋다. 얼마만큼 바꿔갈 것인지에 대한 비율을 나타내는 이름을 주로 머신러닝에서는 learning_rate(학습률)이라고 한다.

#학습률 설정 및 b에 대해서도 동일하게 적용
learning_rate = 1e-2

w = w - learning_rate * loss_rate_of_change_w

loss_rate_of_change_b = \
    (loss_fn(model(t_u, w, b+delta),t_c)) -  \
    (loss_fn(model(t_u, w, b+delta),t_c)) / (2.0 * delta)
    
b = b - learning_rate * loss_rate_of_change_b

분석

여기서 loss_rate_of_change들이 미분의 개념이라는 것을 파악했을지도 모른다.(맞다) 우리는 delta를 0.1로 설정했다. 즉 앞뒤로 0.1 총 0,2만큼 거리의 지점끼리 변화율을 본 것이다. 즉 평균변화율을 관찰했다. 우리가 임의로 설정한 delta는 사실 상대적으로 클 수도 작을 수도 있어 최솟값지점을 크게 뛰어넘을수도 있다. 이 delta를 극한으로 줄이면 어떻게 될까? 고등학교때 배웠던 순간변화율을 표현하게 된다. 즉 그 지점의 미분값이다.

여러개의 파라미터 - 편미분
이전에 표현한 두개의 loss_rate_of_change 값이 존재한다. w, b가 그 예시이다. w와 b가 하나의 값이 아니라 배열이 되어 수많은 값을 가진다고 하였을 때 우리는 고등학교때배운 미분으로는 부족하다. y와 x로만 만들어진 함수의 x에 대한 y미분이 아닌 y와 x,a,b,c....여러가지 파라미터가 존재할 경우 우리는 편미분이 필요하다.

모델 적합을 위한 반복

훈련루프

훈련 샘플을 가지고 반복적으로 파라미터를 조정하는 훈련의 한 단위를 에포크(epoch)라고 한다.

def dloss_fn(t_p, t_c):
    dsq_diffs = 2 * (t_p - t_c) / t_p.size(0)
    return dsq_diffs
def dmodel_dw(t_u, w, b):
    return t_u
def dmodel_db(t_u, w, b):
    return 1.0
def grad_fn(t_u, t_c, t_p, w ,b):
    dloss_dtp = dloss_fn(t_p, t_c)
    dloss_dw = dloss_dtp * dmodel_dw(t_u, w, b)
    dloss_db = dloss_dtp * dmodel_db(t_u, w, b)
    return torch.stack([dloss_dw.sum(), dloss_db.sum()])
def training_loop(n_epochs, learning_rate, params, t_u, t_c):
    for epoch in range(1, n_epochs+1):
        w, b = params        
        t_p = model(t_u, w, b)
        loss = loss_fn(t_p, t_c)
        grad = grad_fn(t_u, t_c, t_p, w, b)        
        params = params - learning_rate * grad
        print('Epoch %d, Loss %f' % (epoch, float(loss)))
    return params

손실값이 매우 커지면서 무한대까지 증가하는 과정을 관찰가능하다. 이는 params 조정이 너무 크다는 신호이며, 최적화는 목표에 수렴하기보다는 발산하게 되는 현상을 보인다. 즉 learning * grad 규모를 적절하게 제한하는 것이 중요해보인다. 1e-3, 1e-4로 학습률을 낮춰서 실행해보도록 한다.

입력 정규화

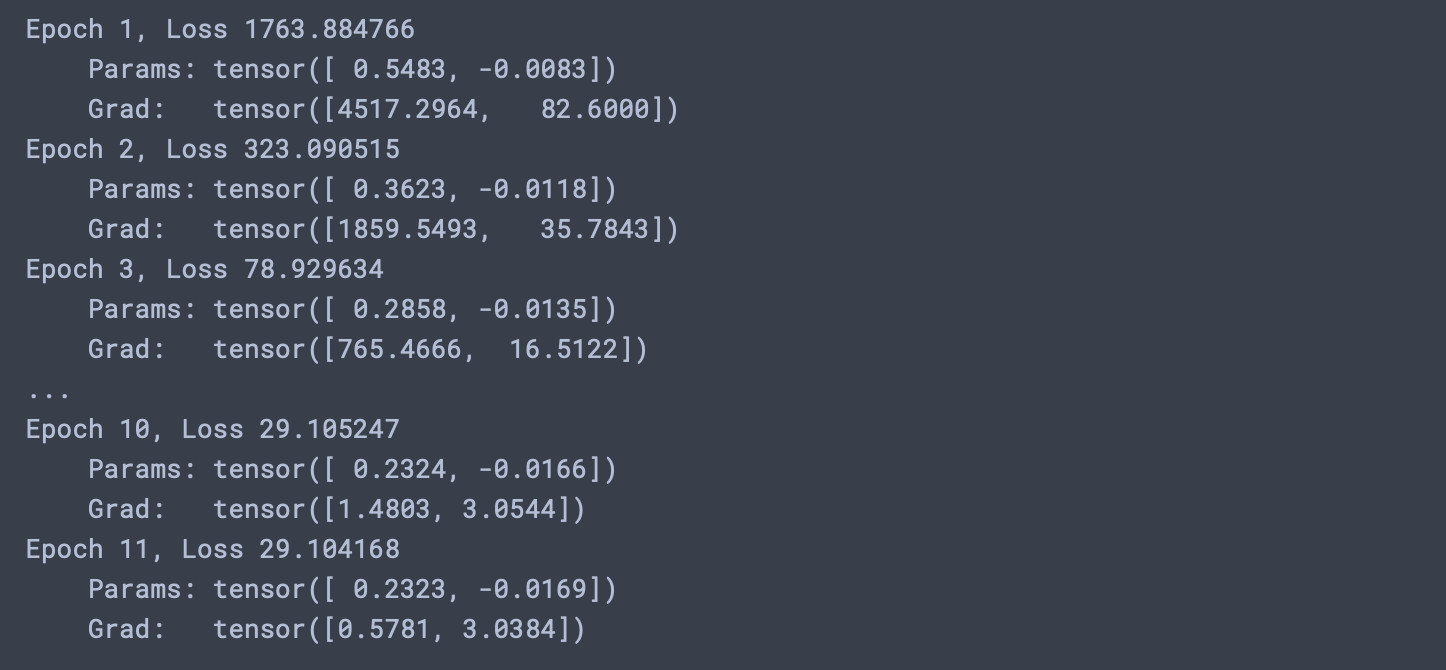
첫 에포크에서 w에 대한 기울기가 b(편향값)에 대한 기울기보다 50배나 큰 것을 볼 수 있다. 즉 가중치와 편향값의 적절한 크기의 학습률은 서로 다르기 때문에 업데이트를 불안정하게 만들 수 있다. 서로 다른 학습률을 부여할 수 있지만 파라미터가 많은 모델이 되어버리기 때문에 세세한 관리가 필요해진다.(자동화 관점에서 bad) 이 경우를 방지하기 위해 우리는 데이터 전처리작업중 하나인 정규화를 진행한다. 입력값을 변경해서 기울기가 서로 큰 차이가 나지 않게 입력값의 범위가 -1.0에서 1.0사이를 벗어나지 않도록 바꿔놓는다. 우리 예제에서는 이를 위해 t_u에 0.1를 곱하면 어느정도 해결된다.

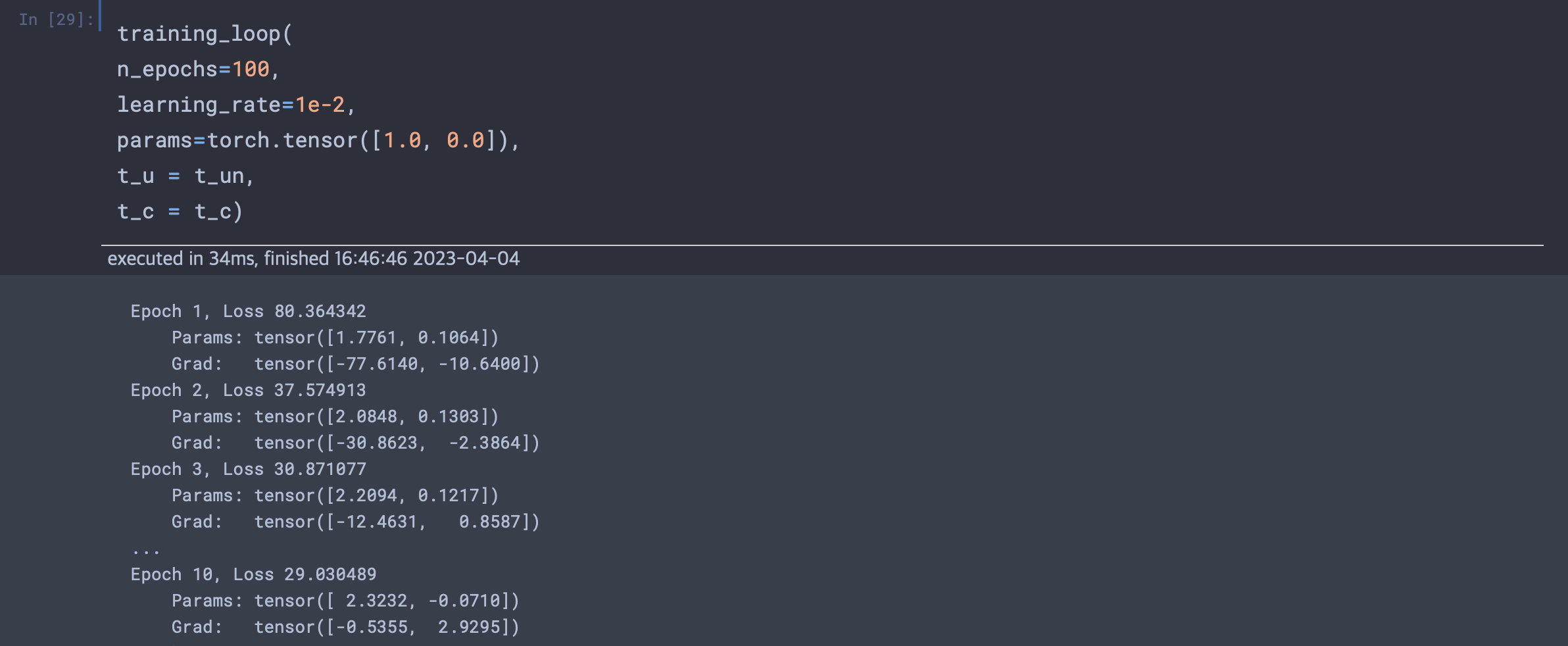
이번에는 학습률을 1e-2로 하여도 발산하는 문제가 발생하지 않았다. 즉 정규화또한 학습률을 작게만들어야 하는 원인으로 작용하였다. 서로의 파라미터끼리의 미분값 차이는 조정에 방해가 되었기 때문에 그런 것으로 추정된다.
이제 params 값의 변화량이 작아질 때까지 루프를 도는 횟수를 충분히 늘리도록 에포크를 5000으로 설정해서 훈련시킨다.

미분값이 0에 거의 수렴하였다. 즉 최솟값에 도달한 것이다. 찾아낸 w값들은 실제의 값인 w=5.5556, b=-17.7778과 거의 비슷하다.

• 이렇게 학습률과 에포크를 조절하며 적절한 학습방법을 찾는 과정을 하이퍼 파라미터 튜닝이라고 한다.

시각화

시작할 때 했던 그대로 데이터를 차트에 그려보자. 선위에 데이터가 존재하는 경우는 없지만 어쨌든 직관적으로 정확한 라인을 그린 모습이다.

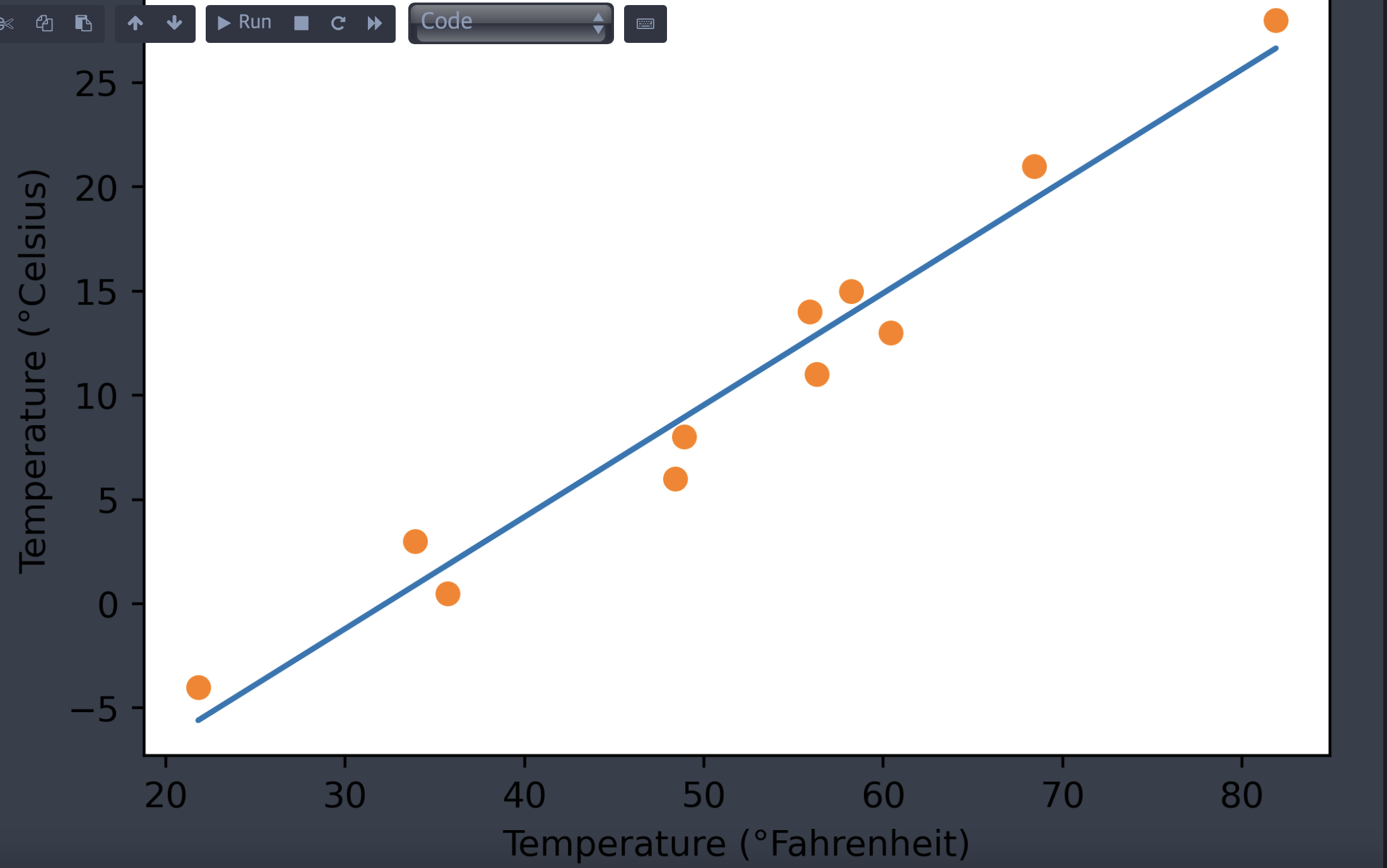
파이토치의 자동미분 : 모든 것을 역전파 하라

앞서 우리는 chain-rule을 사용하여 미분을 역방향으로 전파하는 방법을 w,b를 내부 파라미터로 가지는 모델과 손실에 대한 합성 함수의 기울기를 계산했다. 이 과정의 기본 전제는 우리가 다루는 모든 함수가 해석적으로 미분가능해야 한다는 것이다. 하지만 매우 복잡한 함수들에 대한 미분 표현식을 작성하는 것은 매우 번거롭다

기울기 자동 계산

파이토치 자동미분은 이러한 번거로운 일을 해결해줄 구세주이다. 파이토치 텐서는 자신이 어디로부터 왔는지, 즉 어느 텐서에서 어떤 연산을 수행해서 만들어진 텐서인지 기억하고 있기에 자연스럽게 미분을 최초입력까지 연쇄적으로 적용하여 올라갈 수 있다. 순방향 식만 주어진다면 우리는 기울기를 자동적으로 제공받을 수 있다.

params = torch.tensor([1,0, 0.0], requires_grad = True)

텐서 생성자에 새롭게 보이는 requires_grad 인자는 params에 가해지는 연산의 결과로 만들어지는 모든 텐서를 이은 전체 트리를 기록하라고 파이토치에 요청하는 것이다. 즉 params를 조상으로 두는 모든 텐서는 params로부터 해당 텐서가 만들어지기까지 그 사이에 있는 모든 함수에 접근할 권한을 가진다. 일반적으로 모든 파이토치 텐서는 grad 속성을 가지는데 주로 값은 None이다.

주의
파이토치에서 손실에 대한 미분을 계산하고 값을 텐서의 grad 속성에 누적한다. 여기서 저장이 아니라 누적이라고 한 것을 명심해야한다. backward호출은 미분을 말단 노드에 누적시킨다. 따라서 파라미터 조정을 위해 사용한 후에는 기울기를 명시적으로 다시 0으로 초기화 해야한다.

if params.grad is not None:
	params.grad.zero_()

# 자동 미분 기능을 넣어 만든 트레이닝 루프
def training_loop(n_epochs, learning_rate, params, t_u, t_c):
    for epoch in range(1, n_epochs + 1):
        if params.grad is not None:
            params.grad.zero_()

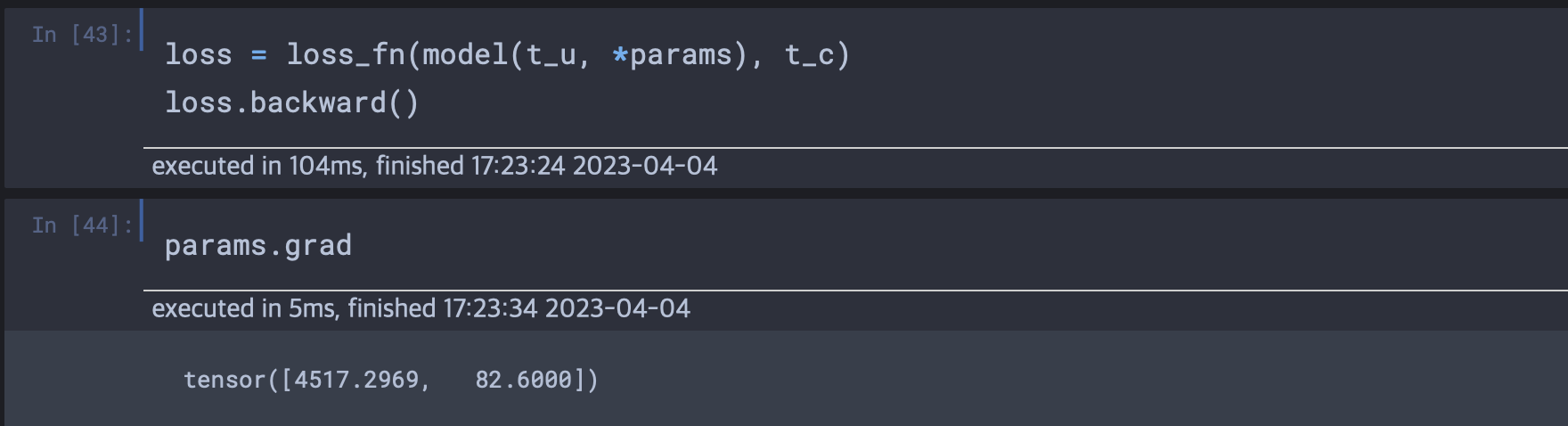
        t_p = model(t_u, *params)  # <1>
        loss = loss_fn(t_p, t_c)
        loss.backward()# grad = grad_fn(t_u, t_c, t_p, w, b) 대신, 

        with torch.no_grad(): # 파라미터 수정
            params -= learning_rate * params.grad

        if epoch % 500 == 0:
            print('Epoch %d, Loss %f' % (epoch, float(loss)))
            
    return params

골라쓰는 옵티마이저

우리는 앞서 최적화를 위해 기본 버전의 경사 하강 로직을 사용했다. 모델이 복잡해질 경우에 수렴을 더 잘 하기위해서 여러가지 최적화 전략과 기법이 존재한다.

모든 옵티마이저는 zero_grad와 step이라는 두 가지 메소드를 제공한다. zero_grad는 옵티마이저 생성자에 전달됐던 파라미터의 모든 grad 속성값을 0으로 만든다. step은 옵티마이저별로 구현된 최적화 전략에 따라 파라미터 값을 조정한다.

import torch.optim as optim
params = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate = 1e-5
optimizer = optim.SGD([params], lr=learning_rate)

SGD는 확률적 경사 하강의 약자로 순정 버전의 경사 하강과 완전히 동일하다. SGD의 기울기는 미니 배치(mini-batch)라고 불리는 여러 샘플 중에서 임의로 뽑은 일부에 대해 평균을 계산해 얻기 때문에 확률적이라고 한다.

t_p = model(t_u, *params)
loss = loss_fn(t_p, t_c)
loss.backward()

optimizer.step()

params
# quiz : 왜 t_u에 대한 grad는 판단하지 않을까?(미분에 대한 이해)

코드를 관찰해보면 우선 우리는 파라미터를 초기화하였고, 학습률을 설정한 뒤 옵티마이저 객체에 파라미터와 학습률을 전달했다. 그 후 순방향 패스를 진행하여 예측값을 생성하고, 손실값을 계산했다. 그리고 미분값을 계산하고, optimizer객체의 메소드인 .step()으로 하여금 params를 조정했다. 훈련루프를 위를 활용하여 다시 코딩해본다.

def training_loop(n_epochs, optimizer, params, t_u, t_c):
    for epoch in range(1, n_epochs + 1):
        t_p = model(t_u, *params) # 예측값 도출
        loss = loss_fn(t_p, t_c) # 손실함수 값 도출
        
        optimizer.zero_grad() # 기울기 계산시 이미 있는 기울기 값 0으로 초기화
        loss.backward() # 기울기 계산
        optimizer.step() # 기울기와 학습률을 가지고 최적화 알고리즘에 따라 params 수정

        if epoch % 500 == 0:
            print('Epoch %d, Loss %f' % (epoch, float(loss)))
            
    return params

훈련, 검증, 과적합

우리는 옵티마이저에게 주어진 데이터 포인트에 대한 손실을 최소화하라고 요청하고 있다. 이 때문에 우리가 손실을 구하거나 음의 기울기를 따라 내려갈 때 사용했던 데이터와는 다른 별개의 데이터를 사용하면 기대했던 것보다 높은 손실값을 얻을 수 있다. 이런 현상을 과적합(overfitting)이라 한다.

과적합 방지를 위해 대응가능한 한 방법으로는 과적합이 일어날 수 있음을 먼저 인지하는 것이다. 데이터에서 일부를 따로 떼어 검증셋으로 두고 남은 데이터로 하여금 모델을 훈련시키긴다. 이제 손실을 한 번은 훈련셋에 대해 구하고, 한 번은 검증셋에 대해 구할 수 있다.
훈련 손실값은 모델이 훈련셋에 얼마나 잘 맞춰졌는지, 즉 훈련데이터에 대해 적합이 잘 되었는지를 판별할 수 있고 검증 손실값 흐름은 모델이 얼마나 일반화가 잘 되었는지를 나타낸다.

과적합 개선 방법
과적합은 데이터에 종속된 모델의 동작이 우리가 근사하는 과정에 대해 실제 문제 해결에 적합한지를 판단하는 데 하나의 장애물로 작용한다. 이를 개선하기 위해서는 충분한 데이터가 주어졌는지를 파악해야하고, 모델이 훈련데이터에 대해 적합한 수준으로 맞춰질 수 있는지에 대한 여부를 파악해야한다. 여러 방법중 하나는 손실 함수에 페널티 항(penalization term)을 두어 모델의 적합이 더 천천히 그리고 부드럽게 만들어지도록 하는 방법이다. 또 하나는 입력 데이터에 대해 노이즈를 추가하는 것이다. 통상적으로 훈련셋과 검증셋은 동일한 양이 아니기 때문에 거의 항상 훈련 손실보다 크다는 사실과, 모델은 훈련셋으로 훈련되기 때문에 훈련 손실이 일반적으로 더 낮을 수 밖에 없다.

자동미분의 주의사항과 자동미분 끄기

앞의 훈련 루프에서 train_loss에 대해서만 backward를 호출한다. 검증 데이터로는 학습을 진행하면 안되기 때문이다. 따라서 역전파는 훈련셋 데이터에 대한 오차만 전파하게 된다. 또한 val_loss는 val_t_u가 본체이기 때문에 val_loss의 기울기 누적은 이루어지지 않는다.

추가적으로 생각해볼 부분이 있다. val_loss에 대해 backward를 호출하지 않으면서 처음에 연산 그래프를 만드는 이유가 무엇일까? 계산을 추적하지 않고서 일반 함수처럼 model과 loss_fn을 호출하면 되지 않을까? 그럼에도 최적화된 자동미분 그래프 생성에는 검증 과정에는 생략해도 되는 비용이 들어간다. 이를 위해 파이토치는 torch.no_grad를 통해 자동미분을 끌 수 있게 해준다.