1일 1로그 100일 완성 IT지식 - 소프트웨어22 <10개 도시를 최단거리로 여행하는 방법>
알고리즘 복잡도
알고리즘의 복잡한 정도를 나타내는 척도로서 수행 시간을 계산한 시간 복잡도와 기억 공간의 소요량을 계산한 공간 복잡도가 있다.
이진 검색
데이터의 양이 증가함에 따라 일의 양이 천천히 늘어난다.
가장 일반적인 경우는 선형, 즉 단순히 N의 복잡도를 가지며, 일의 양이 데이터 양에 정비례한다.
이진 탐색은 위치를 나타내는 변수 3개를 사용하는데 탐색하고자 하는 범위의 시작점, 끝점, 그리고 중간점이다. 찾으려는 데이터와 중간점을 비교하여 중간점보다 작으면 중간점 왼쪽에서 탐색하고, 중간점보다 크면 중간점 오른쪽에서 탐색한다.
- 중간점이 정확히 없다면 한칸 아래에서 시작
예를들어 숫자 21을 찾는다고 가정해보자.
중간점이 정확히 없으니 4에서 시작
1단계
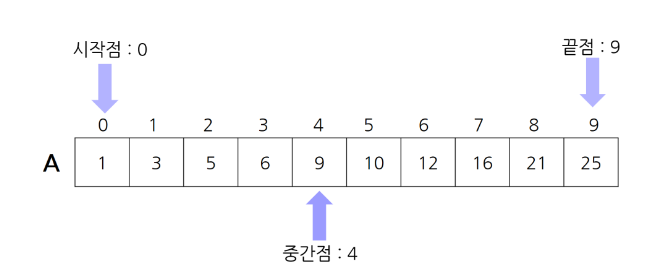
2단계
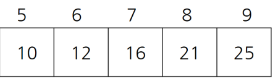
3단계
4단계
21 발견
ex) 100개의 정보에서 1개의 값을 도출하는 과정
퀵 정렬 알고리즘
효율이 낮지만(일의 양이 빠르게 증가)로그 인자가 상당히 느리게 증가하므로 큰 값에도 효과적으로 활용가능하다.
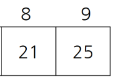
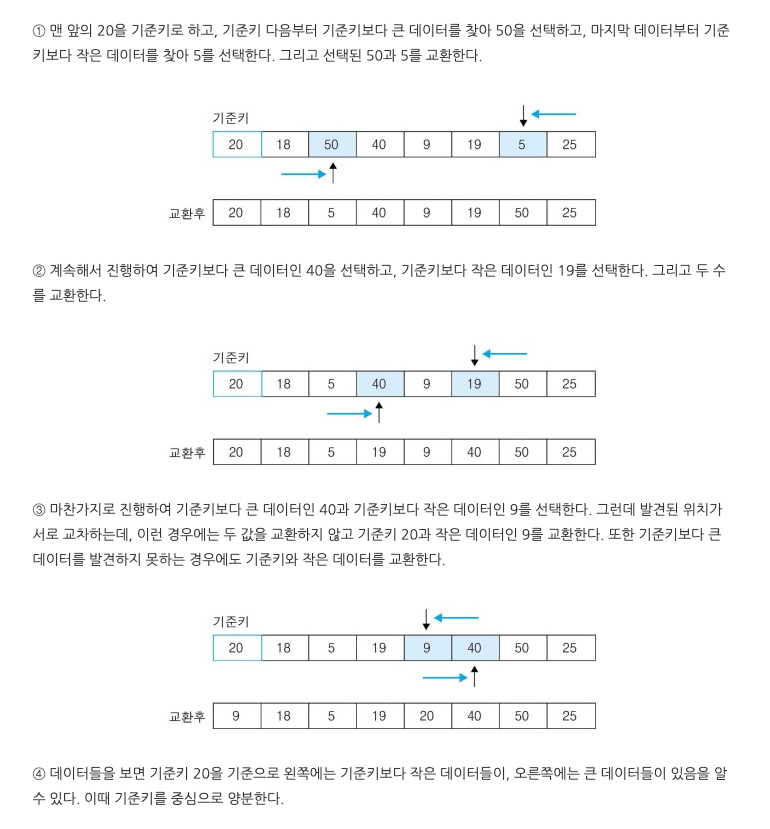
퀵 정렬(quick sort)은 기준키를 기준으로 작거나 같은 값을 지닌 데이터는 앞으로, 큰 값을 지닌 데이터는 뒤로 가도록 하여 작은 값을 갖는 데이터와 큰 값을 갖는 데이터로 분리해가며 정렬하는 방법이다.
N^2는 일의 양이 너무 빨리 늘어나서 실행하기 고역스럽거나 활용이 불가능하다.
이 밖에 다른 복잡도를 갖는 알고리즘도 많지만 너무 심오해서 전문가들만 관심을 가지는 정도이다.
실생활에서 자주 등장하지만 효율이 낮은 중요한 알고리즘이 있다.
지수알고리즘
지수 복잡도로, 2^N의 비율로 증가한다. (N^2와는 다르다)
지수 알고리즘에서는 일의 양이 유난히 빠르게 늘어난다.
사실상 모든 가능한 경우를 하나씩 시도해 봐야만 하는 상황에서 발생
이점 : 암호 기법에 사용되는 알고리즘이 이 기반을 사용하여 문제를 계산상 실행 불가능할 정도로 큰 N을 선택하여 적의 공격을 방지한다.
여행하는 외판원 문제
외판원은 자신이 사는 도시에서 출발해 어떤 순서로든 다른 도시를 모두 방문하고 나서 다시 출발점으로 돌아와야 한다. 여기서 목표는 각 도시를 정확히 한 번씩(반복없이) 방문하고, 전체 여행한 거리를 최소로 만드는 것이다.
통학 버스나 쓰레기차가 다니는 경로를 효율적으로 만드는 일과 아이디어가 같다.
이것을 단순하게 모든 경우를 따져가면서 푼다면 n!의 가짓수를 모두 따져야 한다.
n이 12만 되어도 4억이 넘어간다.
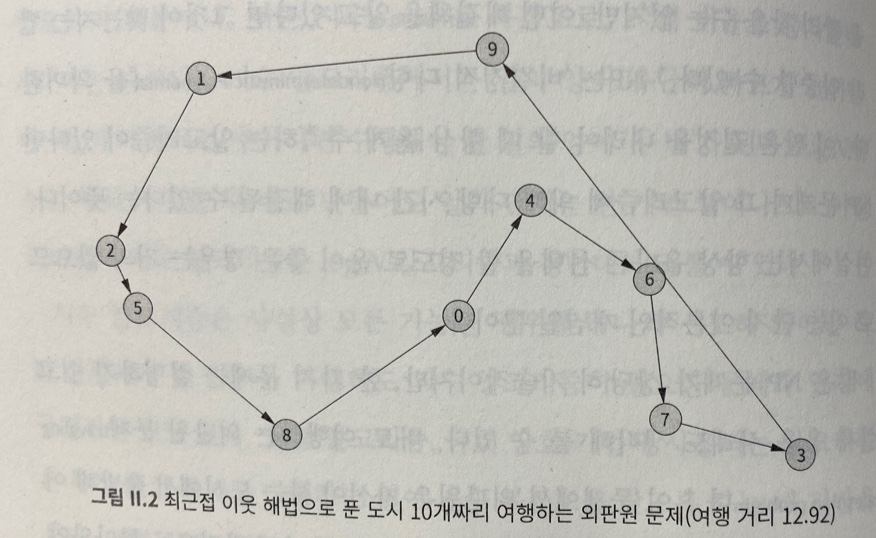
직관적으로 와닿는 '최근접 이웃'
최근접 이웃 : 가장 가까운 점을 찾는 탐색 방법
최상의 해법으로 푼 도시 10개짜리 여행하는 외판원 문제
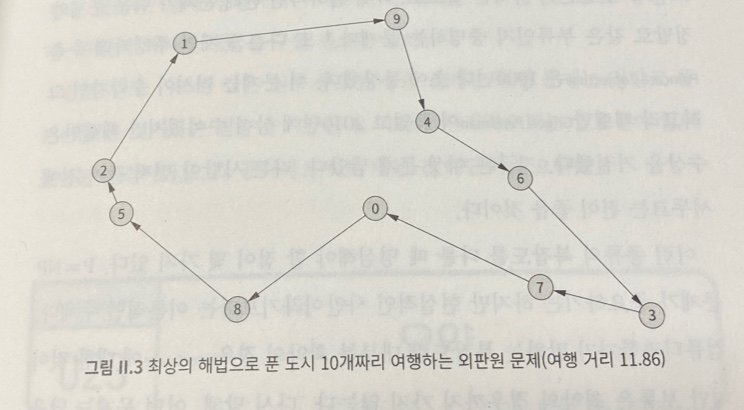
약 18만개 경로 전체를 완전 탐색해서 찾아낸 최단 경로를 보여준다.
여행의 거리는 11.86으로, 가장 짧은 최근접 이웃 경로보다 약 8% 짧다.
요약
가능한 모든 해법을 완전 탐색하는 것이 가장 효율적으로 푸는 방법이다.
문제가 본질적으로 난해해서인지, 아니면 인간이 똑똑하지 못해서 해결책을 알아내지 못한 것인지 모르겠지만, '본질적으로 난해한 것'으로 의견이 기울고 있다.
스티분 쿡은 이런 문제 중 다수가 서로 동등하다는 것을 증명했다. 만약 우리가 그 문제 중 어느 한 문제를 해결하는 다항 시간 알고리즘을 찾을 수 있다면, 이 모든 문제에 대한 다항 시간 알고리즘을 찾아낼 수 있다는 것이다.
여행하는 외판원 문제에서 도시를 10개만 방문한다면 모든 가능한 경로를 시도해 보는 것이 가능하겠지만, 100개는 실행 가능하지 않을 것이고 도시 1,000개는 확실히 불가능하다. 실제 상황에서는 대부분 근사치만 구하는 것으로도 충분하다.
N, logN, N^2, NlogN과 같이 데이터 양과 관련해서 실행 시간을 표현하는 아이디어는 '얼마나 빨리 계산할 수 있는가?'를 정제한 결과다. 알고리즘과 복잡도 연구는 컴퓨터과학의 주요 영역으로, 이론과 실제 적용 모두 중요한 연구 대상이다.
컴퓨터과학에서는 어떤 문제가 계산 가능하고 어떤 것이 그렇지 않은지, 어떻게 하면 빨리 계산할 수 있는지, 메모리를 필요 이상으로 사용하지 않고 계산할 수 있는지, 혹은 처리 속도와 메모리 소비 간 균형을 유지하면서 계산할 수 있는지에 관심을 둔다.
