그래프 탐색 알고리즘
탐색: 많은 양의 데이터에서, 원하는 데이터를 찾는 과정
→ DFS BFS 유형이 대표적
먼저 알아야 할 내용
자료구조 - 스택 / 큐
생략
재귀 함수
: 자기 자신을 다시 호출하는 함수
ex) 팩토리얼, 유클리드 호재법: gcd(b, a%b)
-
DFS를 실질적으로 구현하고자 할 때 자주 사용되는 방법 중 하나이므로 잘 이해해야 함
-
파이썬에는 최대 재귀 깊이 제한 함수가 있음 → 오류 메시지와 함께 종료됨
→ 재귀 함수 종료 조건 반드시 명시해야 함 -
잘 활용하면 복잡한 알고리즘 간결하게 작성 가능
-
모든 재귀 함수는 반복문을 이용해 동일한 기능 구현 가능
-
재귀 함수가 반복문보다 유리한 경우도 있고 불리한 경우도 있음
-
컴퓨터가 함수를 연속적으로 호출하면 컴퓨터 메모리 내부의 스택 프레임에 쌓임
→ 스택을 사용해야 할 때, 스택 라이브러리 대신 재귀 함수 사용하는 경우 多
DFS (Depth-First Search)
: 깊은 부분 우선 탐색
스택 자료구조 (or 재귀함수) 이용
- 탐색 시작 노드 스택에 삽입 후 방문 처리
- 스택 최상단 노드에, 방문하지 않은 인접한 노드가
하나라도 있다면 그중 기준에 맞는 하나의 노드를 스택에 삽입 후 방문 처리
없으면 스택에서 최상단 노드 꺼내기- 2번 과정 더 수행할 수 없을 때까지 반복
최대 재귀 깊이 제한
DFS 문제 풀이 중 런타임 에러가 걸리는 흔한 이유 중 하나가 최대 재귀 깊이 제한 때문!
sys.setrecursionlimit(10 ** 8) 으로 챙겨줘야 한다
예제
방문 기준: 번호가 낮은 인접 노드부터
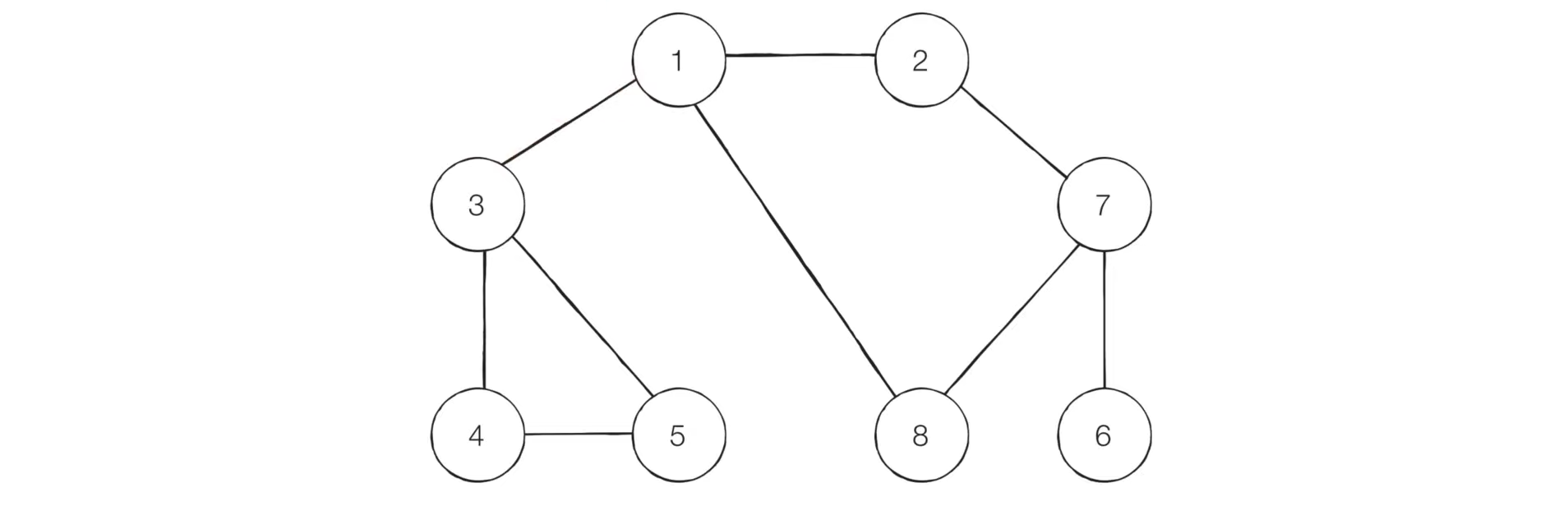
- 시작 노드 1을 스택에 삽입 (방문 처리)
stack : 1 방문: 1 - 최상단 노드인 1에 방문하지 않은 인접 노드로 2, 3, 8이 있으므로 번호가 낮은 2를 먼저 삽입 후 방문 처리
stack : 1 2 방문: 1 - 2 - 최상단 노드인 2에 방문하지 않은 인접 노드로 7이 있으므로 삽입 후 방문 처리
stack : 1 2 7 방문: 1 - 2 - 7 - 최상단 노드인 7에 방문하지 않은 인접 노드로 6, 8이 있으므로 번호가 낮은 6을 먼저 삽입 후 방문 처리
stack : 1 2 7 6 방문: 1 - 2 - 7 - 6 - 최상단 노드인 6에 방문하지 않은 인접 노드가 없으므로 스택에서 6 꺼내기
stack : 1 2 7 방문: 1 - 2 - 7 - 6 - 최상단 노드인 7에 방문하지 않은 인접 노드로 8이 있으므로 삽입 후 방문 처리
stack : 1 2 7 8 방문: 1 - 2 - 7 - 6 - 8 - 최상단 노드인 8에 방문하지 않은 인접 노드가 없으므로 스택에서 꺼내기
stack : 1 2 7 방문: 1 - 2 - 7 - 6 - 8 - 최상단 노드인 7에 방문하지 않은 인접 노드가 없으므로 스택에서 꺼내기
stack : 1 2 방문: 1 - 2 - 7 - 6 - 8 - 최상단 노드인 2에 방문하지 않은 인접 노드가 없으므로 스택에서 꺼내기
stack : 1 방문: 1 - 2 - 7 - 6 - 8 - 최상단 노드인 1에 방문하지 않은 인접 노드로 3이 있으므로 삽입 후 방문 처리
stack : 1 3 방문: 1 - 2 - 7 - 6 - 8 - 3 - 최상단 노드인 3에 방문하지 않은 인접 노드로 4가 있으므로 삽입 후 방문 처리
stack : 1 3 4 방문: 1 - 2 - 7 - 6 - 8 - 3 - 4 - 최상단 노드인 4에 방문하지 않은 인접 노드로 5가 있으므로 삽입 후 방문 처리
stack : 1 3 4 5 방문: 1 - 2 - 7 - 6 - 8 - 3 - 4 - 5 - 최상단 노드 5 → 4 → 3 → 1 순으로 방문하지 않은 인접 노드가 없으므로 모두 스택에서 나오고 끝
stack : 방문: 1 - 2 - 7 - 6 - 8 - 3 - 4 - 5
예제 구현 코드
def dfs(graph, now, visited):
visited[now] = True # 현재 노드 방문 처리
print(now, end = ' ') # 방문 순서 출력용
# 현재 노드의 인접 노드를 재귀적으로 방문
for node in graph[now]:
if not visited[node]: # 방문하지 않은 노드면
dfs(graph, node, visited) # 방문
# __main__
# 각 노드가 연결된 정보를 2차원 리스트로 표현
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6 ,8],
[1, 7]
]
# 각 노드가 방문된 정보를 1차원 리스트로 표현
visited = [False] * 9
# 정의된 DFS 함수 호출
dfs(graph, 1, visited)BFS (Breadth-First Search)
: 너비 우선 탐색 → 그래프에서 가까운 노드부터 우선적으로 탐색
-
큐 자료구조 이용
-
방문하지 않은 노드를 모두 한 번에 삽입한다는 점에서 DFS랑 다름
-
특정 조건에서의 최단 경로 문제를 해결할 때 효과적으로 사용됨
- 탐색 시작 노드를 큐에 삽입하고 방문 처리
- 큐에서 노드 꺼낸 뒤에, 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리
- 2번 과정 수행할 수 없을 때까지 반복
예제
- 시작 노드 1 큐에 넣고 방문 처리
queue: (out) 1 (in) 방문: 1 - 1을 꺼내고, 1의 방문하지 않은 인접 노드 2, 3, 8을 모두 넣고 방문 처리, 단 번호 작은 2부터 넣음
queue: 2 3 8 방문: 1 - 2 - 3 - 8 - 2를 꺼내고, 2의 방문하지 않은 인접 노드 7을 넣고 방문 처리
queue: 3 8 7 방문: 1 - 2 - 3 - 8 - 7 - 3을 꺼내고, 3의 방문하지 않은 인접 노드 4, 5를 모두 넣고 방문 처리, 단 번호 작은 4부터 넣음
queue: 8 7 4 5 방문: 1 - 2 - 3 - 8 - 7 - 4 - 5 - 8을 꺼내고, 방문하지 않은 인접 노드가 없으므로 꺼내기만 하고 무시
queue: 7 4 5 방문: 1 - 2 - 3 - 8 - 7 - 4 - 5 - 7을 꺼내고, 7의 방문하지 않은 인접 노드 6을 넣고 방문 처리
queue: 5 4 6 방문: 1 - 2 - 3 - 8 - 7 - 4 - 5 - 6 - 5 → 4 → 6 순으로 방문하지 않은 인접 노드가 없으므로 모두 큐에서 나오고 끝
queue: 방문: 1 - 2 - 3 - 8 - 7 - 4 - 5 - 6
정리
1번 노드로부터 거리가 가까운 순으로,
-
거리가 1인 2, 3, 8번이 먼저 방문
-
그다음으로 거리가 2인 7, 4, 5번이 방문되고
-
거리가 3으로 가장 먼 6이 가장 나중에 방문된다는 점에서
각 간선의 비용이 모두 동일한 상황에서의 최단 거리 문제를 해결하기 위해 사용되는 경우가 많음
예제 구현 코드
from collections import deque
def bfs(graph, start, visited):
queue = deque([start]) # 큐 자료구조 이용
visited[start] = True # 현재 노드 방문 처리
# 큐가 빌 때까지 반복
while queue:
# 큐에서 원소 하나 뽑아 출력
now = queue.popleft()
print(now, end = ' ')
# 방문하지 않은 인접 노드를 큐에 모두 삽입
for node in graph[now]:
if not visited[node]:
queue.append(node)
visited[node] = True
# __main__
# 각 노드가 연결된 정보를 2차원 리스트로 표현
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6 ,8],
[1, 7]
]
# 각 노드가 방문된 정보를 1차원 리스트로 표현
visited = [False] * 9
# 정의된 DFS 함수 호출
bfs(graph, 1, visited)Source
이코테 2021 강의 몰아보기