🔧변경내용🔨

제목	날짜	내용
발행일	23.04.05

📌들어가기에 앞서

해당 포스트는 Brute-Force Algorithm을 학습한 것을 정리한 내용입니다.

컴퓨터 과학에서 Brute Force는 시행착오 방법론을 말한다. 그리고 암호학에서도 이 용어를 사용한다.

암호학에서는 Brute Force Attack이라고 불리며 특정한 암호를 풀기 위해서 모든 값을 대입하는 방법을 말한다.

• 수많은 시행착오를 통해 민감한 데이터를 해킹하는 방법
• 무차별 대입 공격이 다른 해킹 방법과 다른 점은 지능형 전략을 사용하지 않는 점
• 무차별 대입 공격은 올바른 조합을 찾을 때까지 다양한 조합을 시도하는 것

예를 들어 0-9 사이의 4자리 숫자로 된 자물쇠가 있다고 가정해 보자.

• 이 자물쇠의 번호 조합은 잊어버렸지만 튼튼해서 다른 자물쇠로는 바꾸고 싶지 않다.
• 자물쇠를 사용하려면 비밀번호를 0000부터 9999까지의 경우의 수를 모두 하나하나 대입하여 자물쇠를 열어야 한다.
• 이때 최악의 경우 10000번의 시도가 필요하다.

이렇게 하나하나 대입하여 시도하는 방법이 Brute Force Attack다.

---

🌈 Brute Force Algorithm

Brute Force Algorithm은 무차별 대입 방법을 나타내는 알고리즘

순수한 컴퓨팅 성능에 의존하여 모든 가능성을 시도하여 문제를 해결하는 방법

Brute Force는 최적의 솔루션이 아니라는 것을 의미

공간복잡도와 시간복잡도의 요소를 고려하지 않고 최악의 시나리오를 취하더라도 솔루션을 찾으려고 하는 방법을 의미한다.

Brute Force Algorithm은 크게 두 가지 경우에 사용

• 프로세스 속도를 높이는 데 사용할 수 있는 다른 알고리즘이 없을 때

• 문제를 해결하는 여러 솔루션이 있고 각 솔루션을 확인해야 할 때

예를 들어 어떤 문서 중에서 ‘leekoby’ 이란 문자열을 찾아야 한다고 가정해 보자.

이때, 사전과 같이 모든 단어가 정렬되어 있다면 이진 탐색 알고리즘을 이용하여 절반씩 범위를 줄일 수 있다.

모든 단어 n에 대해 시간복잡도는 O(logn)이 될 수도 있다.

하지만 문서는 사전처럼 정렬되어 있지 않다.

목표 단어 ‘leekoby’에 도달하려면 각 단어를 반복해서 비교해야 한다.

시간복잡도는 O(n)과 같다.

이처럼 Brute Force Algorithm은 문제에 더 적절한 해결 방법을 찾기 전에 시도하는 방법이다.

그러나 데이터의 범위가 커질수록 상당히 비효율적이다.

프로젝트의 규모가 커진다면 더 효율적인 알고리즘을 사용해야 한다.

---

💢 Brute Force Algorithm의 한계

Brute Force Algorithm은 문제의 복잡도에 매우 민감한 단점이 있다.

문제가 복잡해질수록 기하급수적으로 많은 자원을 필요로 하는 비효율적인 알고리즘이 될 수 있다.

여기서 자원은 시간이 될 수도 있고 컴퓨팅 자원이 될 수도 있다.

일반적으로 문제의 규모가 현재 자원으로 충분히 커버가 가능한 경우에 Brute Force Algorithm을 사용힌다.

만약 이를 벗어난 경우는 정확도를 조금 희생하고 더 효율적인 알고리즘을 사용한다.

---

💻Brute Force Algorithm을 어디서 사용하고 있을까?

Brute Force Algorithm은 많은 곳에서 사용하고 있다.

지금까지 풀었던 문제를 돌아보면 Brute Force Algorithm을 사용해서 풀었던 문제들도 있다.

반복문을 통해서 범위를 줄이지 않고 하나하나 비교하는 것도 Brute Force Algorithm일 것이다.

어떻게 활용되는지 살펴보자.

---

순차 검색 알고리즘 (Sequential Search)

배열 안에 특정 값이 존재하는지 검색할 때 인덱스 0부터 마지막 인덱스까지 차례대로 검색한다.

검색 키 K를 사용하여 순차 검색을 구현
입력: n개의 요소를 갖는 배열 A와 검색 키 K
출력: K 값과 같은 요소 인덱스 또는 요소가 없을 때 -1

function SequentialSearch2(arr, k) {
	
	let n = arr.length;    // 현재의 배열 개수를 n에 할당
 	arr[n] = k;            // 검색 키를 arr n 인덱스에 할당
	let i = 0;             // while 반복문의 초깃값을 지정
 	while (arr[i] !== k) { // 배열의 값이 k와 같지 않을 때까지 반복
		i = i + 1;           // k와 같지 않을 때 i를 +1 
	}
	if (i < n) {     // i가 k를 할당하기 전의 배열개수보다 적다면(배열 안에 k 값이 있다면)
		return i;      // i를 반환
	} else {
		return -1;     // -1을 반환
	}
}

---

문자열 매칭 알고리즘 (Brute-Force String Matching)

길이가 n인 전체 문자열과 길이가 m인 문자열 패턴을 포함하는지를 검색한다.

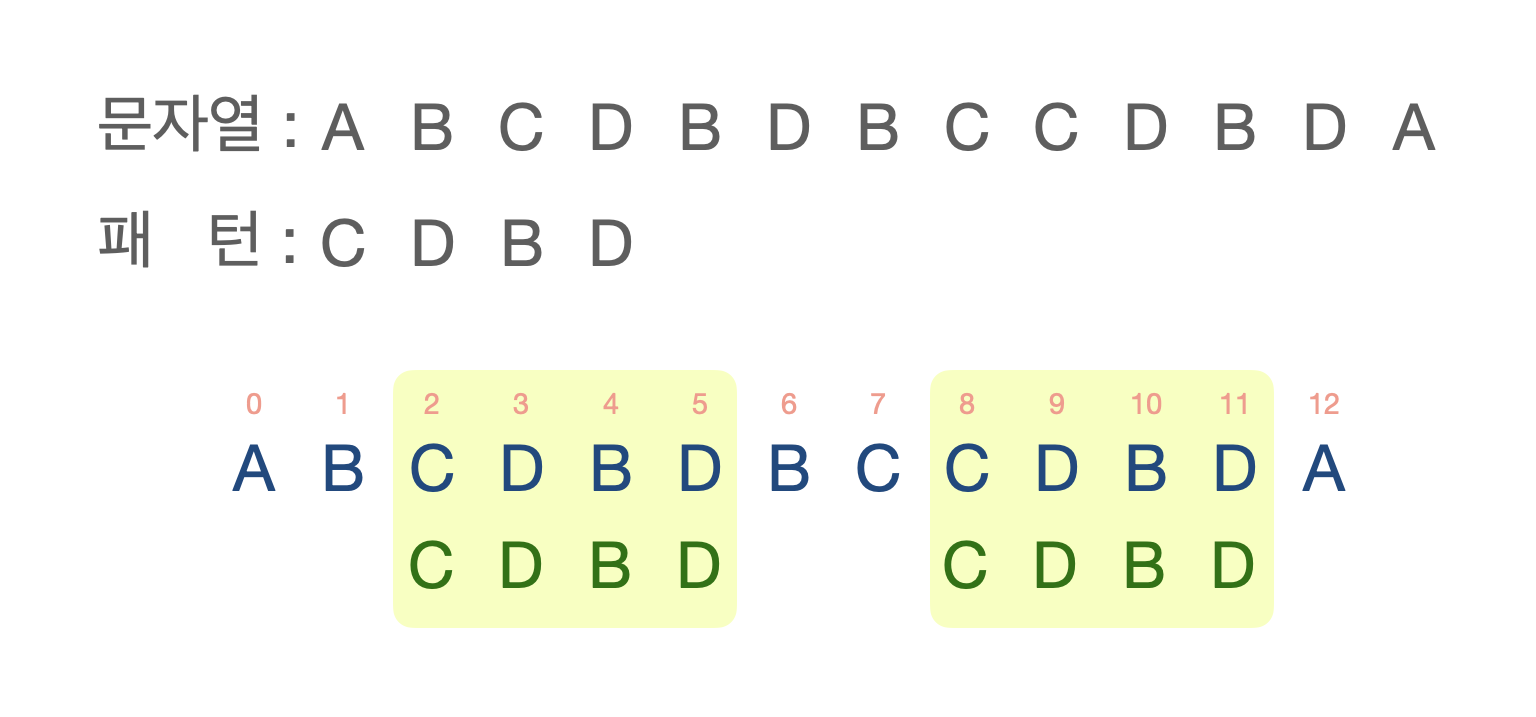
Brute Force 문자열 매칭을 구현.
입력: n개의 문자 텍스트를 나타내는 배열 T, m개의 문자 패턴을 나타내는 배열 P
출력: 일치하는 문자열이 있으면 첫 번째 인덱스를 반환, 검색에 실패한 경우 -1을 반환

function BruteForceStringMatch(arr, patternArr) {
  let n = arr.length;
  let m = patternArr.length;
  for (let i = 0; i <= n - m; i++) {
  // 전체 요소 개수에서 패턴 개수를 뺀 만큼만 반복 
  //그 수가 마지막 비교 요소이기 때문
  // i 반복문은 패턴과 비교의 위치를 잡는 반복문
    let j = 0;
    // j는 전체와 패턴의 요소 하나하나를 비교하는 반복문
    while (j < m && patternArr[j] === arr[i + j]) {
      // j가 패턴의 개수보다 커지면 안 되기 때문에 개수만큼만 반복
      // 패턴에서는 j 인덱스와 전체에서는 i + j 인덱스의 값이 같은지 판단
      // 같을 때 j에 +1 
      j = j + 1;
    }
    
    if (j === m) {
	// j와 패턴 수가 같다는 것은 패턴의 문자열과 완전히 같은 부분이 존재한다는 의미
    // 이때의 비교했던 위치를 반환
      return i;
    }
  }
  return -1;
}

---

선택 정렬 알고리즘 (Selection Sort)

전체 배열을 검색하여 현재 요소와 비교하고 컬렉션이 완전히 정렬될 때까지 현재 요소보다 더 작거나 큰 요소(오름차순 또는 내림차순에 따라)를 교환하는 정렬 알고리즘

주어진 배열을 Selection Sort로 오름차순 정렬합니다.
입력: 정렬 할 수 있는 요소의 배열 A
출력: 오름차순으로 정렬된 배열

function SelectionSort(arr) {
   for (let i = 0; i < arr.length - 1; i++) {
  // 배열의 0번째 인덱스부터 마지막인덱스까지 반복.
  
    // 현재 값 위치에 가장 작은 값 할당
    let min = i;
     
    // 현재 인덱스를 최솟값의 인덱스를 나타내는 변수에 할당
    for (let j = i + 1; j < arr.length; j++) {
    // 현재 i에 +1을 j로 반복문을 초기화하고 i 이후의 배열요소와 비교하는 반복문을 구성
      if (arr[j] < arr[min]) {
      // j 인덱스의 배열 값이 현재 인덱스의 배열 값보다 작다면
        min = j;
        // j 인덱스를 최소를 나타내는 인덱스로 할당
      }
    }
    // 반복문이 끝났을 때(모든 비교가 끝났을 때)
    // min에는 최솟값의 인덱스가 들어있다.
    // i 값과 최솟값을 바꿔서 할당
    let temp = arr[i];
    arr[i] = arr[min];
    arr[min] = temp;
  }
	// 모든 반복문이 끝나면 정렬된 배열을 반환
  return arr;
}

---

더 알아볼 내용

• 그 밖의 Brute Force 활용 알고리즘

  • 버블 정렬 알고리즘 - Bubble Sort

  • Tree 자료 구조의 완전 탐색 알고리즘 - Exhausive Search (BFS, DFS)

  • 동적 프로그래밍 - DP(Dynamic Programing)

• 더 공부하면 좋은 키워드

  • Brute Force vs Dynamic Programing

  • Closet-Pair Problems by Brute Force

  • Convex-Hull Problems by Brute Force

---

📚 레퍼런스