Date: 2024.11.09.

I. 서론

우리 학교의 알고리즘 학회 0&1에서 주최하는 알고리즘 대회에 참가했다.

상위 4명이 수상받고, 상위 10명까지 아주대학교, 경희대학교, 성균관대학교, 인하대학교, 한국항공대학교, 한양대학교 ERICA (+ 단국대학교(?))의 '경인지역 대학 연합 프로그래밍 대회 Shake!'에 학교 대표 출전 자격을 부여받는다.

나는 1년 전에 참가했던 [대회] 2023 컴퓨터학부 주관 신입생 알고리즘 대회에서 내 실력에 대해 너무 아쉬움을 느껴서 solved.ac 기준 브론즈1쯤에서 현재 골드 5까지 자료구조와 알고리즘을 공부하며 올라왔다. 작년에 참가했던 대회는 신입생 대회였기 때문에 그래도 부담이 없었는데, 이번 대회는 전 학년 재학생이 참여할 수 있는 대회였다. 그래서, 우리 학교의 PS를 잘하는 실력자들이 많이 참여할 것으로 예상하여 참가에 의의를 두고 출전했다. 대부분 0&1 학회원분들 인 것 같았는데, 그래도 나와 비슷한 수준이거나 초보분들도 많이 참여한 것 같았다. 결론적으로는 나는 29명이 참가해서 8등을 하여 Shake!의 출전자격은 얻은 것 같으나, 수상을 하지는 못했다.

이번에도 대회에서 문제를 풀면서 아쉬움이 많이 남았는데, 대회 당시에 못 풀었지만, 내가 풀 수 있었을 만한 문제들을 풀이해보면서 다음 기회를 노려보고자 한다.

최종 4등 분이 2문제 solve 였기 때문에 대회 당시에도 '한 문제만 더 풀면되는데...' 하며 아쉬움이 많이 남았었다. B번이나, H번이나 대회에서는 어려워보였는데 다시 공부하면서 보니까 풀만했던 문제들이었다. 반대로, 오히려 접근 방법이 생각났던 C번은 난이도가 있던 문제였다.

나는 대회에 가면 이러한 선택들을 잘 못해서 항상 좋지 못한 결과를 보이는 것 같다. 이러한 부분은 계속 대회에 출전해보고, 더 많이 PS를 연습해보면서 발전해 나갈 수 있을 문제라고 생각한다. 1년 사이에 발전한 만큼, 다음 대회에서는 수상할 수 있도록 더 열심히 공부해야 겠다는 자극을 얻은 좋은 기회였던 것 같다.

A번 당구 좀 치자 제발 (32642) (브론즈 4)

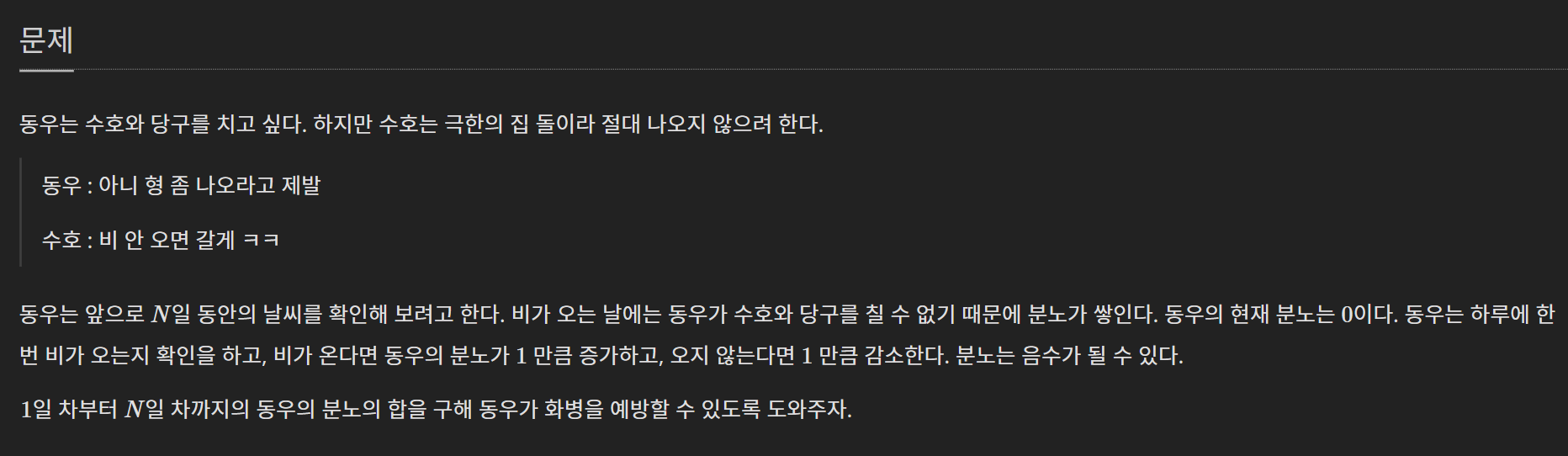
문제

입출력

풀이

import sys

input = sys.stdin.readline
s = []
b = 0 

n = int(input())

weather = list(map(int, input().split()))

for i in weather:
    if i == 0:
        b -= 1
        s.append(b)
    else:
        b += 1
        s.append(b)

print(sum(s))

이 문제는 쉽게 풀 수 있는 문제이다.

나는 처음에 마음이 급했던 탓인지 n일차까지 분노의 합을 구하라고 했는데, 분노의 결과값을 구하는 것으로 잘못 해석해서 한번 둘러갔다. 이러한 일이 없으면 빠르게 풀 수 있을 것이다.

B번 정민이의 수열 제조법 (32643) (실버 1)

문제

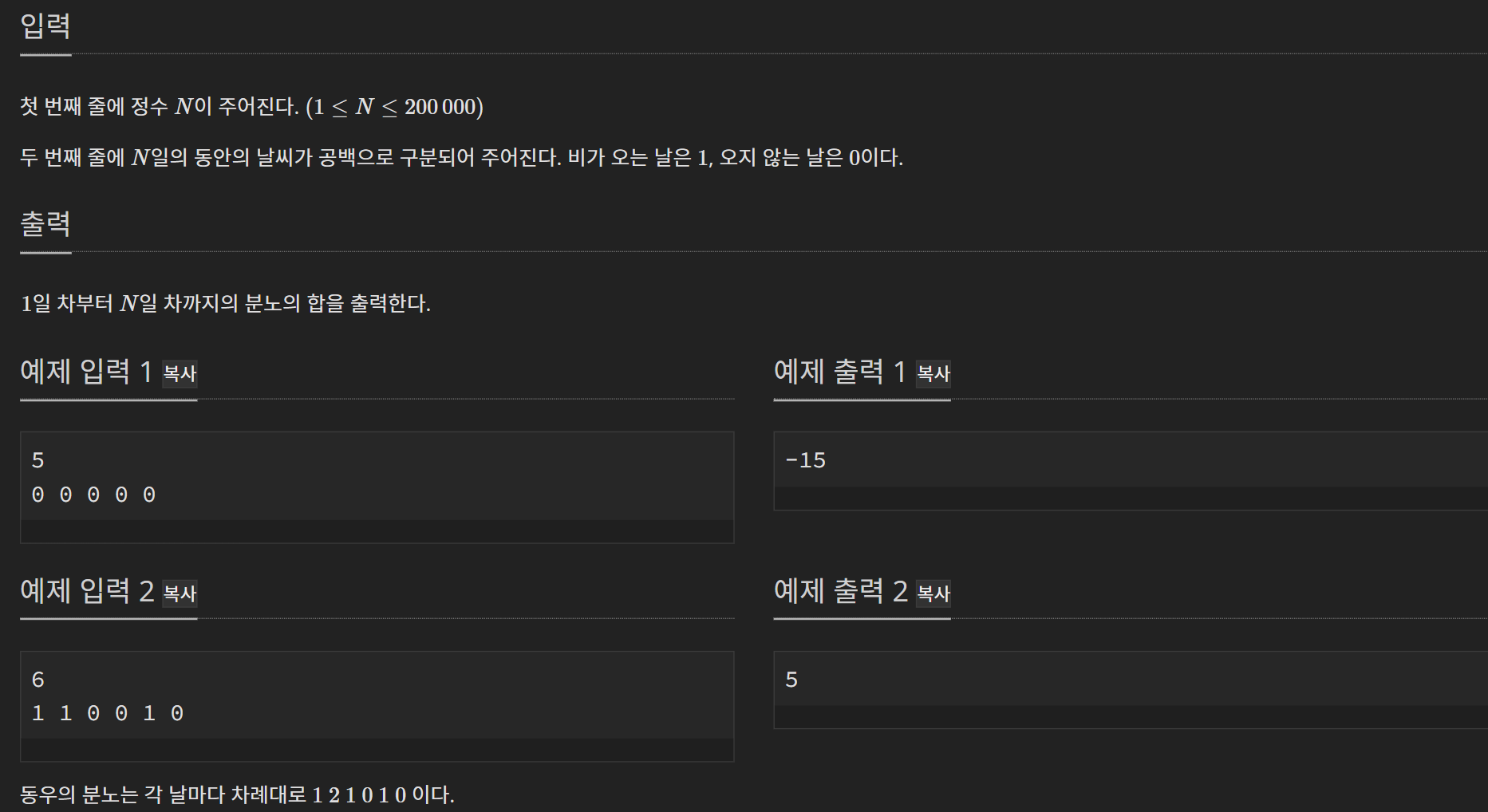
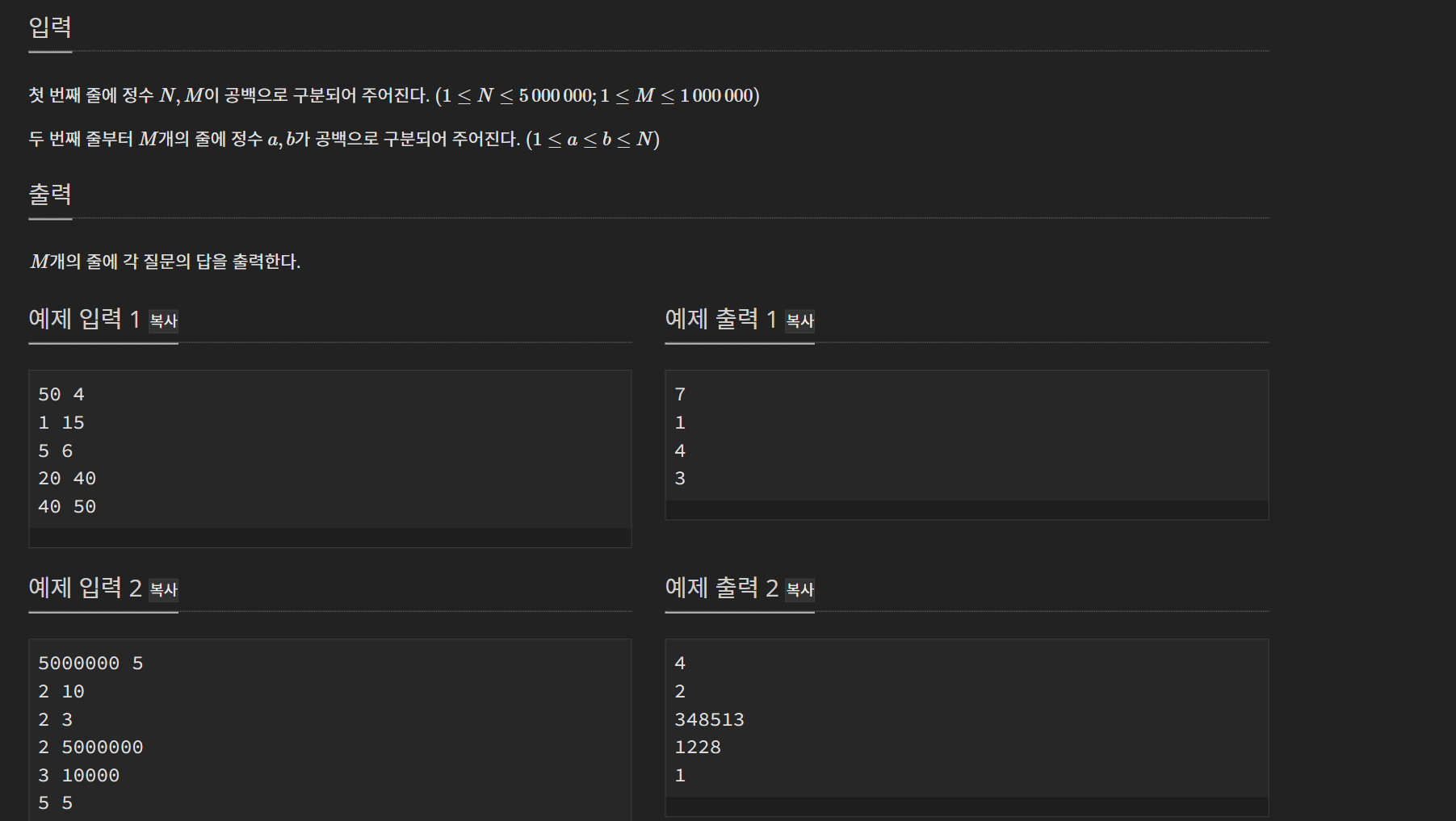
입출력

풀이

대회 당시에는 문제를 이해는 했는데, 어떻게 풀어야할지 감이 안잡혀서 패스했다.

문제 자체가 제곱한 수와 곱한 수로 설명을 해서 '어떻게 접근해야 하지' 싶을 수 있다. 그런데, 수열을 직접 써보면서 생각해보면 어떻게 접근할 지 알 수 있었다.

먼저, 한 정수를 제곱한 수라는 것은 자기 자신을 2번 곱함을 의미한다. 즉, 수열에 추가되는 수는 어떠한 수를 곱해서 나올 수 있는 수인 것이다. 반대로 말하면, 기존에 있어야 하는 수는 1을 포함한 소수여야한다는 것이다. 소수를 결합해 합성수를 만들어 1~n까지의 모든 수를 표현할 수 있는 것이다. 다르게 말해보면, 모든 수를 소인수 분해하면 소수의 곱으로 만들 수 있다는 것이다. 따라서 이 문제는 1~n까지의 소수를 구하고, a, b 구간에 해당하는 소수를 구하면 된다.

하지만, 이 문제는 1초 시간 제한이 있기 때문에 $O(n^2)$이 불가하다. 이 말은, 정의를 기반으로 한 기존의 소수 구하는 방법으로는 시간 초과 때문에 구할 수 없다는 것이다. 따라서, '에라토스테네스의 체' 라는 1~n까지의 소수를 빠르게 구할 수 있는 방법을 사용해서 구해야한다. 하지만, 이것 만으로는 제 시간안에 돌아가지 않았는데, 이는 M의 범위 때문이다. $1 \leq M \leq 1,000,000$ 이기 때문에 만약 리스트 슬라이싱을 통해 count를 하는 경우 $O(M^2)$ 만큼 시간을 더 쓰면서 시간 초과가 난다. 그래서 나는 초반 시간이 조금 소요되더라도 최악의 경우에 더 빨리 사용할 수 있도록 누적합 배열을 만들어 놓고, b 구간의 소수 갯수 - a구간의 소수 갯수 해서 구해줬다. 그리고, 디테일하게는 범위가 a 이상, b이하이기 때문에 a, b 둘 다 포함해야한다. 하지만, (5, 5) 같은 입력이 들어왔을 때 같은 값 - 값은 값이니까 0이 나온다. 그래서 이러한 경우까지 포함해주기 위해 a-1 구간의 소수 갯수로 구해줬다.

*에라토스테네스의 체 내용 참고([CS] Python 알고리즘 정리)

import math
import sys

input = sys.stdin.readline

n, m = map(int, input().split())

arr = [1] * (n+1)

for i in range(2, int(math.sqrt(n))+1): # 에라토스테네스의 체
    if arr[i]:
        for j in range(2*i, n+1, i):
            arr[j] = 0

for i in range(1, len(arr)): # 누적합 
    arr[i] += arr[i-1]

for i in range(m):
    a, b = map(int, input().split())

    print(arr[b]-arr[a-1])

C번 랜덤 넘버 추측하기 (32644) (골드 1)

문제

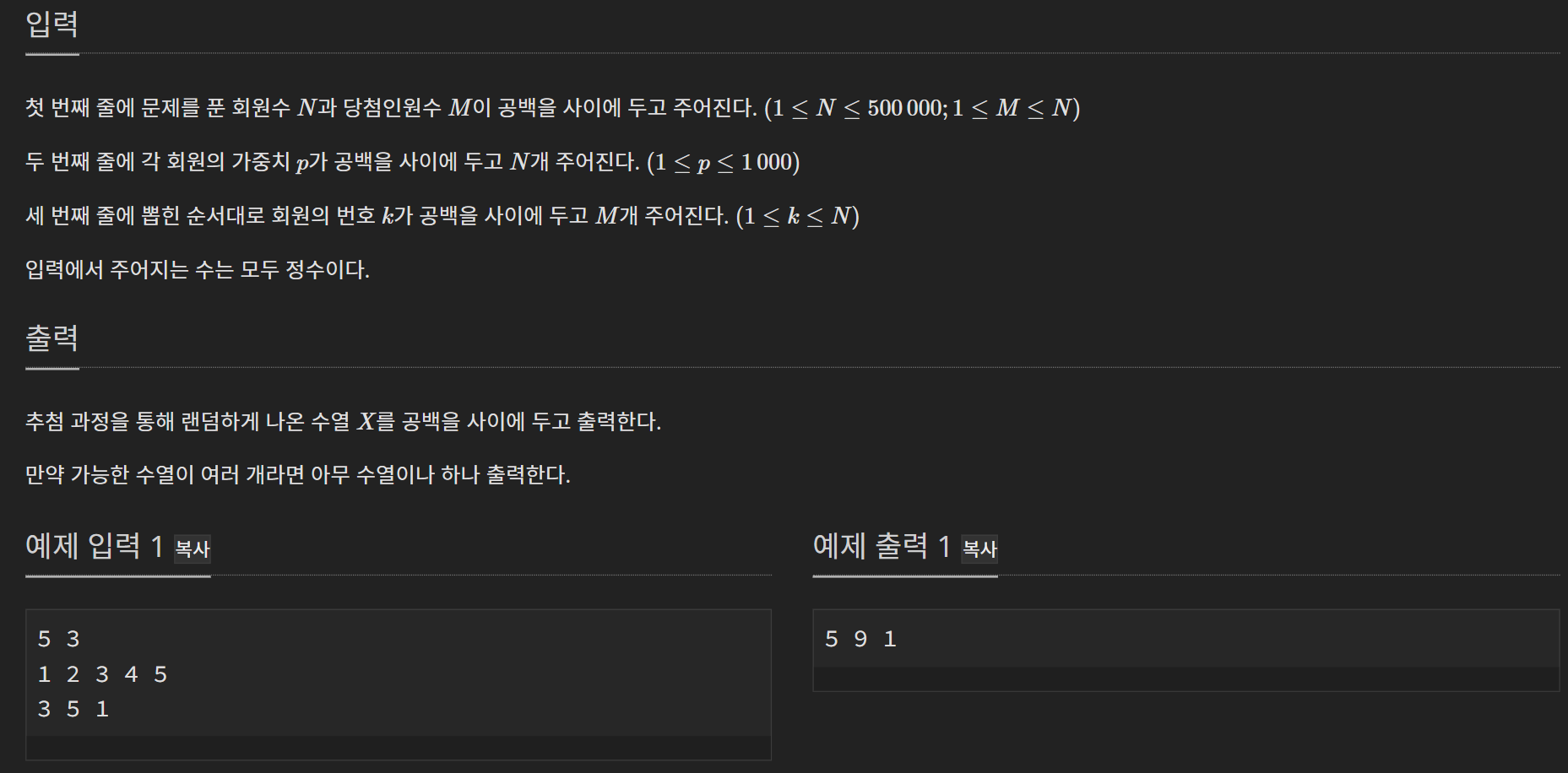
입출력

풀이

당시 스코어보드에서 상위권분들이 A번 이후 C번을 풀어서 C번이 쉬운 난이도라고 생각하여 도전했다. 문제 자체는 천천히 필기하면서 보면 이해가 됐었다. 여기서 총 3시간 중에 2시간 30분을 사용했는데, 시간초과가 나서 결국에는 못 풀었다. 나는 기존의 내 코드를 개선해 나가면 해결될 줄 알았어서 중첩되는 반복문도 줄이고, List 슬라이싱이나 pop 등의 함수로 시간을 많이 쓰는 부분을 계속해서 줄이고, 기존의 정보를 사용할 수 있으면 사용하는 등의 최적화를 해 나갔다. 하지만, 대회가 15분 정도 남았을 때는 내 코드가 더 이상 개선할 점이 보이지 않았고, 다른 접근 방식으로 했어야함을 깨달았지만 다른 문제를 풀기에는 이미 늦었었다.

1) 대회 당시 풀이 (시간초과)

import sys

input = sys.stdin.readline

n, m = map(int, input().split())
p = list(map(int, input().split()))
k = list(map(int, input().split()))

index = []
c = 0

for i in range(n):
    index.append(c)
    c += p[i]

for i in range(m):
    tmp = index[k[i]-1]

    for j in range(i): # O(n^2)
        if k[j] < k[i]:
            tmp -= p[k[j]-1] # - length
    
    print(tmp+1, end=' ')

위 코드는 대회가 15분 남았을 때까지 계속해서 최적화 해나간 코드이다. $O(n^2)$인 for 중첩문을 해결하지 않는 이상 답이 없었다.

Naive한 접근

1. p에 맞춰 W 리스트를 만든다.
2. k의 각 원소 대해 W에서 첫번재 index를 찾는다.
3. p의 해당 k 원소로 접근한 값이 길이가 된다.
4. 길이 만큼 W 리스트에서 첫번째 index를 pop으로 반복해서 제거해 준다.
5. W에서 k의 각 원소에 해당하는 index를 찾아서 + 1해주고 출력.
6. 2~5 과정을 k의 원소의 갯수인 m번 시행하면 된다.

매우 비효율적인 방법이다. 따라서, 나는 다음과 같이 수정했다.

수정한 접근

1. 각각 회원이 처음으로 나오는 index는 이전 가중치의 누적합과 같다는 것을 바탕으로 index 리스트를 정의한다.
2. 각각의 k 원소에 대해 처음 index를 구한다.
3. 각 k원소의 index에서 이전 k원소의 영향을 받는 만큼 빼주고 출력한다.
4. 2~3 과정을 k의 원소 갯수인 m번 시행하면 된다.

1번의 '회원이 처음으로 나오는 index는 이전 가중치의 합과 같다'는 것은 다음의 예로 이해할 수 있을 것이다.
ex. n이 3일 때, p가 2, 1, 3이라면 1번의 index는 0, 2번의 index는 2, 3번의 index는 3이다.

3번의 '이전 k원소의 영향을 받는다'는 것은 다음과 같다.

한 k 원소에 대해 k안에 이전의 자기보다 작은 k 원소가 있다면 가중치만큼 영향을 받는 것이다. 큰 원소만 있었거나, 없었다면 영향을 받지 않는 것이다.

여기서, 영향을 받았다는 것은 각 원소에서 이전 원소 중 작은 원소의 가중치만큼 빼주는 것을 의미한다. 이는 list pop 을 해주지 않고, 계산만으로 지워진 척하기 위해 고안한 방법이었다.

예를 들어, k = 3, 5, 1일 때,
여기서 3은 이전 원소가 없으므로 영향을 받지 않는 것이고, 5는 3에서 3의 크기만큼 지워졌으므로, 3에 영향을 받는 원소이다. 1은 이전 원소가 모두 크므로 영향을 받지 않는 원소이다.

하지만,

이렇게 많이 줄였음에도 시간초과가 났고, 이 문제에 대한 올바른 접근은 처음 인덱스가 이전 가중치의 누적합과 같은 것과 Segment Tree를 이용해서 빠르게 누적합을 구함으로써 쉽게 풀 수 있다고 설명해주셨는데, 아직 Segment Tree를 PS에 사용할 만큼 완전히 공부해보지 않아서 이해하지 못했다. Segment Tree를 배운 다음에 풀어볼 수 있다면 도전해볼 생각이다.

H번 GLCCDM(32649) (실버 3)

문제

입출력

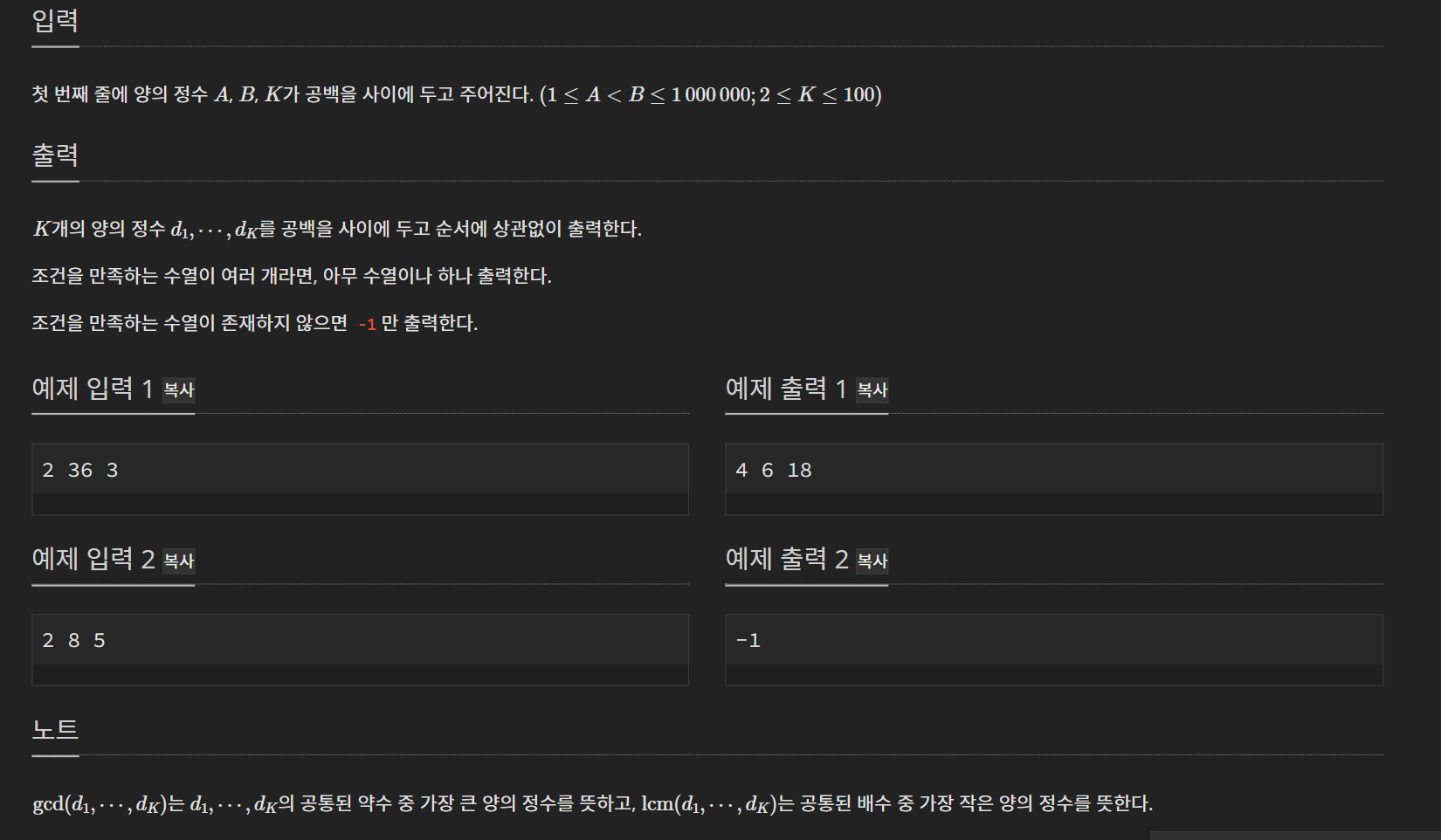
풀이

대회때는 시간 초과 함정이 있는 문제라고 생각했어서 문제만 이해하고, 시도해보려다가 포기했다. 내가 대회때 햇갈렸던 부분은 예제 출력1 때문이었다. 출력 자체는 이해 할 수 있었는데, 저 값을 뽑아내려면 2의 배수, 36의 약수로 줄여도 k개의 for 중첩문으로 다 확인해야할 것 같아서 시간초과가 날 것 같았다. 이 부분이 함정이었다.

import sys

input = sys.stdin.readline

a, b, k = map(int, input().split())

l = []

for i in range(2*a, b, a):
    if b % i == 0:
        l.append(i)

if len(l) + 2 < k:
    print(-1)
else:
    print(a, b, end=' ')

    for i in range(k-2):
        print(l[i], end=' ')
        

나의 접근은 다음과 같다.

1. a의 배수, b의 약수들을 찾는다.
2. a, b가 포함된 수열은 반드시 gcd, lcm이 각각 a, b임이 성립한다.
3. a의 배수, b의 약수를 동시에 만족하는 수의 갯수 + 2 < k이면, 수열로 표현할 수 없다.
4. 아닌 경우에는 a의 배수, b의 약수를 동시에 만족하는 수 중 k-2개를 뽑아서 아무거나 출력한다.

gcd, lcm이 각각 a, b가 되려면 a, b가 직접적으로 들어가 있을 때 반드시 성립할 수 밖에 없다. 이는 조건을 만족하는 수열이 여러개라면 아무 수열이나 출력하라는 조건이 있기 때문에 이 접근이 가능하다.

따라서, a의 배수와 b의 약수를 동시에 만족하는 수의 갯수와 a, b의 갯수인 2를 더했을 때 k보다 작다는 것은 표현할 수 없음을 의미하는 거고, k개 이상이라면 a, b를 출력한 후 a의 배수와 b의 약수를 동시에 만족하는 수 중 아무거나 k개까지 뽑아내서 출력하면 된다.