
✏️ 서론
어제 배웠던 서로소 집합에 이어 오늘은 크루스칼(kruskal)과 위상정렬(topology_sort)을 배워보자.
크루스칼을 알기 위해서는 신장트리(spanning_tree)를 알고 있어야하는데, 얕게 훑어보자.
📍 spanning_tree(신장트리)
신장 트리는 그래프 알고리즘 문제로 자주 출제되는 문제 유형이다.
기본적으로 신장 트리(spanning_tree)란, 하나의 그래프가 있을 때 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프를 의미한다.
이때, 모든 노드가 포함되어 서로 연결되면서 사이클이 존재하지 않는다는 조건은 트리의 성립조건이기도 하다.
트리 자료구조는 노드가
N개 일때, 항상 간선의 개수는N-1개이다.
✏️ 본론
📍 kruskal_algorithm(크루스칼 알고리즘)
크루스칼 알고리즘은 다양한 문제 상황에서 가능한 한 최소한의 비용으로 신장 트리를 찾아야 할 때가 있다.
예를 들어, N개의 도시에서 두 도시 사이에 도로를 놓아 전체 도시가 서로 연결될 수 있게 도로를 설치하는 경우에서, 2개의 도시 A, B를 선택했을 때, 도시 A에서 B로 이동하는 경로가 반드시 존재해야한다.
이때, 모든 도시를 연결할 때 최소한의 비용으로 연결하려면 어떤 알고리즘을 사용해야 할까? 와 같은 문제에서 크루스칼을 이용하면 효율적으로 답을 구할 수 있다.
짧게나마 예시를 들었는데, 이처럼 3개의 노드와 간선이 있다고 가정했을때, 한 노드에서 다른노드를 가는 비용이 최소일때는 23 + 13 = 36인 경우가 있다.
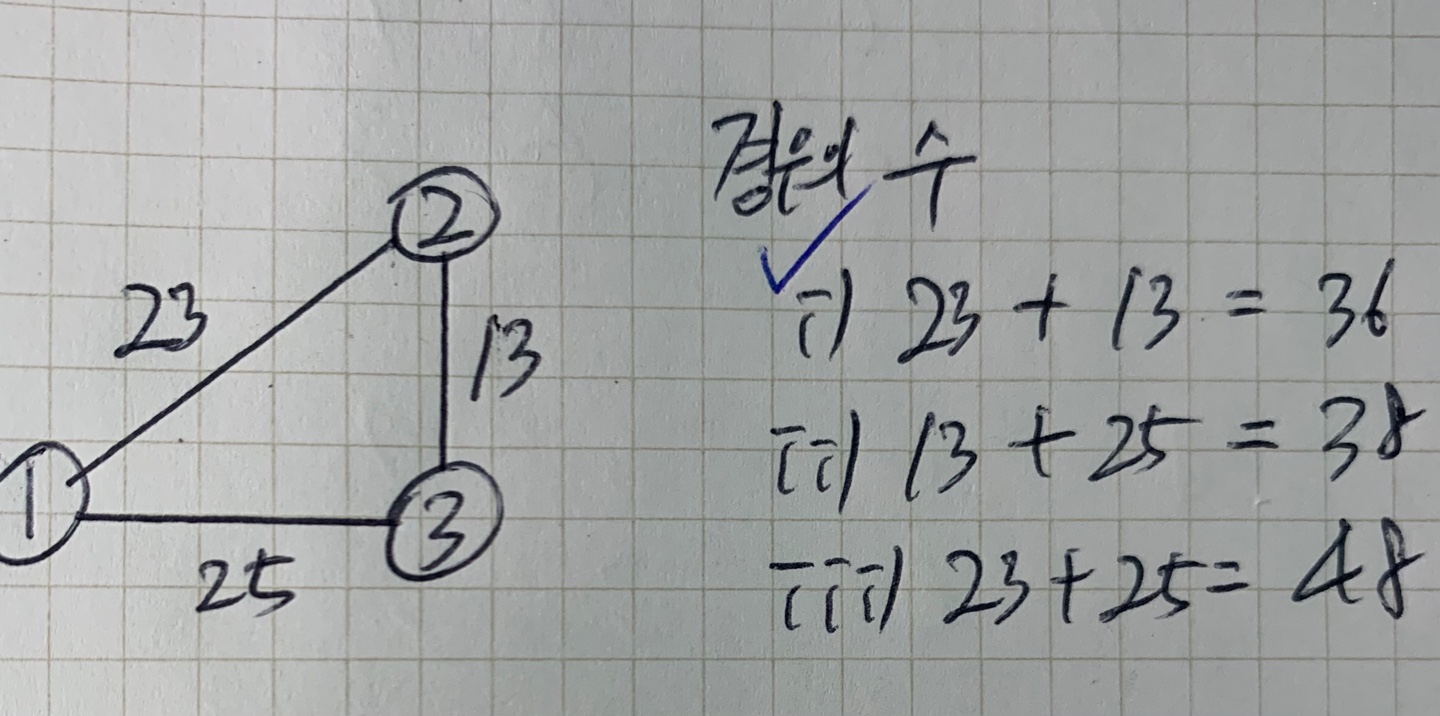
이처럼 신장 트리 중에서 최소 비용으로 만들 수 있는 신장트리를 찾는 알고리즘을 최소 신장트리 알고리즘이고 또 이를 활용하는 대표적인 알고리즘이 크루스칼 알고리즘인 것이다.
알고리즘의 핵심 원리는 다음과 같다.
- 간선 데이터를 비용에 따라 오름차순으로 정렬한다.
- 간선을 하나씩 확인하며 현재의 간선이 사이클을 발생시키는지 확인한다.
- 사이클이 발생하지 않는 경우 최소 신장 트리에 포함시킨다.
- 사이클이 발생하는 경우 최소 신장 트리에 포함시키지 않는다.
- 모든 간선에 대하여 2번의 과정을 반복한다.
시간복잡도는 다음과 같다.
간선의 개수가
E개 일때,O(ElogE)
- 간선을 정렬하는 작업의 시간복잡도가
O(ElogE)이기 때문이다.- 서로소 집합 알고리즘 시간 복잡도 < 정렬 시간복잡도
'''
7 9
1 2 29
1 5 75
2 3 35
2 6 34
3 4 7
4 6 23
4 7 13
5 6 53
6 7 25
'''
def find_parent(parent, x):
if parent[x] != x:
return find_parent(parent, parent[x])
else:
return parent[x]
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
v, e = map(int, input().split())
parent = [0] * (v+1)
edges = []
result = 0
for i in range(1, v+1):
parent[i] = i
for i in range(e):
a, b, cost = map(int, input().split())
edges.append((cost, a, b))
edges.sort()
for edge in edges:
cost, a, b = edge
if find_parent(parent, a) != find_parent(parent, b):
union_parent(parent, a, b)
result = result + cost
print(result)
👉🏽 159여기서 최소 신장트리에 포함되어 있는 간선의 비용만 모두 더하면, 그 값이 최소의 비용에 해당한다.
📍 topology_sort(위상정렬)
위상 정렬은 순서가 정해져 있는 일련의 작업을 차례대로 수행해야 할 때 사용할 수 있는 알고리즘이다. 즉, 방향 그래프의 모든 노드를 방향성에 거스르지 않도록 순서대로 나열하는 것이다.
위상정렬의 알고리즘은 다음과 같다.
- 진입차수가 0인 노드를 큐에 넣는다.
- 큐가 빌 때까지 다음의 과정을 반복한다.
- 큐에서 원소를 꺼내 해당 노드에서 출발하는 간선을 그래프에서 제거한다.
- 새롭게 진입차수가 0이 된 노드를 큐에 넣는다.
이때, 모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재한다고 판단할 수 있다. 다시말해, 큐에서 원소가 V번 추출되기 전에 큐가 비어버리면 사이클이 발생한 것이다.
위상 정렬의 시간복잡도는 O(V + E)이다.
차례대로 모든 노드를 확인하면서, 해당 노드에서 출발하는 간선을 차례대로 제거해야한다. 결과적으로 노드와 간선을 모두 확인하는 측면에서 O(V + E)의 시간이 소요되는 것이다.
'''
7 8
1 2
1 5
2 3
2 6
3 4
4 7
5 6
6 4
'''
from collections import deque
v, e = map(int, input().split())
graph = [[] for _ in range(v+1)]
indegree = [0] * (v+1)
for i in range(e):
a, b = map(int, input().split())
graph[a].append(b)
indegree[b] = indegree[b] + 1
def topology_sort():
q = deque()
result = []
for i in range(1, v+1):
if indegree[i] == 0:
q.append(i)
while q:
now = q.popleft()
result.append(now)
for i in graph[now]:
indegree[i] = indegree[i] - 1
if indegree[i] == 0:
q.append(i)
for i in result:
print(i, end=' ')
topology_sort()
👉🏽 1 2 5 3 6 4 7 위상정렬은 DAG(direct_acyclic_graph): 순환하지 않는 방향그래프의 특징을 지니고 있고 정답이 1가지 이상인 경우도 있다.
또한, 위상정렬을 구현할때 stack을 이용한 DFS로도 구현할 수 있다.
✏️ 결론
이렇게해서 기타 그래프 이론까지 알아봤다.
내일 기타그래프 문제를 풀게되면 알고리즘을 본격적으로 공부한지 약 30일을 채우게된다.
이 책의 들어가기 전에를 보면 책을 볼때 최단경로 문제처럼 상대적으로 어려운 알고리즘을 만나면 한번에 완벽하게 이해하려 하지말고 여러 번 읽어 체화시키는것과 총 3번에 걸쳐 읽고, 각 시간을 30시간, 20시간, 10시간으로 쪼개서 점점 속도를 올리는 방법을 권했다.
이제 이론을 1번 읽었으니 나머지 2번이 남은셈이다.
다음에 또 이론을 읽을때는 지금 걸렸던 속도보다 50% 가량 빨라졌으면 좋겠다.
