기본 개념

💡 소수는 1과 자기 자신만을 약수로 가지는 1보다 큰 자연수

소수를 구하는 방법

1. 단순 나누기

소수 여부를 판단하기 위해 2부터 그 수의 제곱근까지 모든 숫자로 나눠보는 것.

제일 직관적이고, 이해하기 쉽다. 작은 범위의 소수를 구할때는 이렇게 냅다 나누기가 가장 편하다.

⇒ 만약 어떤 수로 나누어 떨어지지 않는다면 그 수는 소수 !

public static boolean isPrime(int num) {
    if (num <= 1) return false; // 1보다 작거나 같은 수는 소수가 아님
    for (int i = 2; i * i <= num; i++) { // 2부터 num의 제곱근까지 나눠봄
        if (num % i == 0) return false; // 나눠 떨어지면 소수가 아님
    }
    return true; // 나눠 떨어지지 않으면 소수
}

• num 이 소수인지 아닌지 판단을 해보자.
• 먼저, 1 이하의 숫자는 소수가 아니기 때문에 false를 반환한다.
• 그 다음에 2부터 num의 제곱근까지 나누어 본다. 만약 num이 어떤 수로 나누어 떨어진다면 false를 반환하고, 그렇지 않으면 true를 반환한다.

장점은 당연히 코드를 보고 단순하게 이해하기 쉽다는 것. 하지만 큰 범위의 숫자에 대해서는 비효율적이다. 예를 들어, 1부터 1,000,000,000까지의 소수를 찾는다고 생각해보면.. 음 네..

시간복잡도

---

2. 에라토스테네스의 체 (Sieve of Eratosthenes)

그래서 좀 더 빨리 소수만 걸러낼 수 있는 방법을 에라토스테네스는 찾았나보다. 이 체는 다음과 같은 방식으로 작동한다.

1. 2부터 시작하여, 그 수의 배수를 모두 제거
2. 그 다음 소수에 대해 같은 작업을 반복
3. 더 이상 배수를 제거할 수 없을 때까지 이 과정을 계속 진행

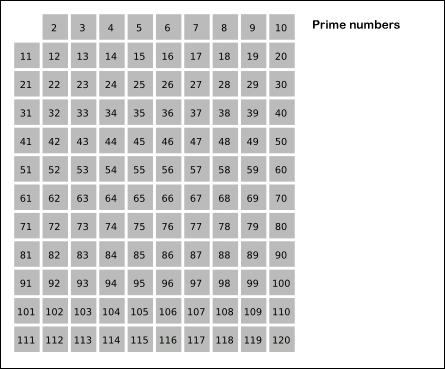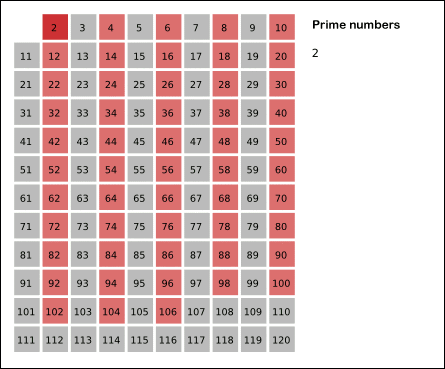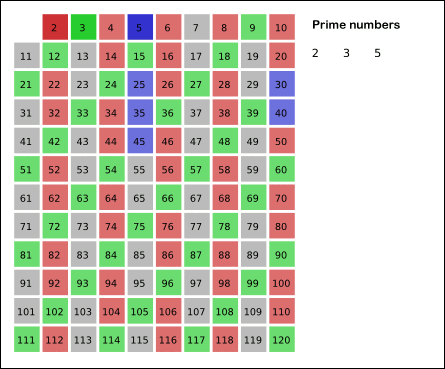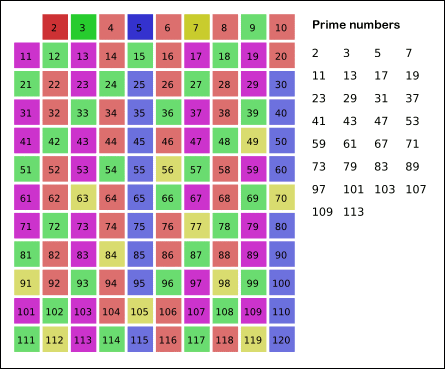
위의 애니메이션을 통해 방식이 이해가 됐다면 코드로 작성해보자.

public static boolean[] sieveOfEratosthenes(int max) {

    boolean[] isPrime = new boolean[max + 1];
    Arrays.fill(isPrime, true); // 배열을 모두 true로 초기화
    isPrime[0] = isPrime[1] = false; // 0과 1은 소수가 아님

    for (int i = 2; i * i <= max; i++) { // 2부터 시작
        if (isPrime[i]) { // i가 소수라면
            for (int j = i * i; j <= max; j += i) {
                isPrime[j] = false; // i의 배수를 false로 설정
            }
        }
    }
    return isPrime;
}

• max까지의 모든 소수를 구한다.
• isPrime 배열의 각 인덱스는 그 숫자가 소수인지 아닌지 판별 → true면 소수, false면 소수가 아님

시간 복잡도

---

주어진 범위 [M, N]에서 소수구하기

주어진 범위 내에서 소수를 모두 구하는 문제를 풀어야 하므로 에라토스테네스의 체 방식을 택해서 문제를 풀었다. 메소드 구현 자체를 N까지의 소수를 모두 배열에 담는 형식으로 해 놓았으니 시작점만 M으로 하여 범위내의 소수(=isPrime 배열)을 반환해주면 된다.

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        
        StringTokenizer stk = new StringTokenizer(br.readLine(), " ");
        int M = Integer.parseInt(stk.nextToken());
        int N = Integer.parseInt(stk.nextToken());
        
        boolean[] isPrime = sieveOfEratosthenes(N);
        
        for (int i = M; i <= N; i++) {
            if (isPrime[i]) {
                bw.write(i + "\n");
            }
        }
        
        bw.flush();
        bw.close();
        br.close();
    }

    public static boolean[] sieveOfEratosthenes(int max) {
        boolean[] isPrime = new boolean[max + 1];
        Arrays.fill(isPrime, true);
        isPrime[0] = isPrime[1] = false; // 0과 1은 소수가 아님
        
        for (int i = 2; i * i <= max; i++) {
            if (isPrime[i]) { // i가 소수라면
                for (int j = i * i; j <= max; j += i) {
                    isPrime[j] = false; // i의 배수를 소수가 아니라고 표시
                }
            }
        }
        
        return isPrime;
    }
}

• 사용자가 범위 [M, N]을 입력
• 에라토스테네스의 체를 사용해 2부터 N까지의 모든 소수를 판별
• M부터 N까지의 수를 반복하면서, 소수로 판별된 수를 출력

---

만약 단순 나눗셈으로 소수 구하기 코드를 작성한다면?

  import java.io.*;
  import java.util.*;
  
  public class Main {
      public static void main(String[] args) throws IOException {
          BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
          BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
          
          StringTokenizer stk = new StringTokenizer(br.readLine(), " ");
          int M = Integer.parseInt(stk.nextToken());
          int N = Integer.parseInt(stk.nextToken());
          
          for (int i = M; i <= N; i++) {
              if (isPrime(i)) {
                  bw.write(i + "\n");
              }
          }
          
          bw.flush();
          bw.close();
          br.close();
      }
  
      // 단순 나누기 방법으로 소수를 판별하는 메서드
      public static boolean isPrime(int num) {
          if (num <= 1) return false; // 1 이하의 수는 소수가 아님
          for (int i = 2; i * i <= num; i++) { // 2부터 num의 제곱근까지 반복
              if (num % i == 0) return false; // 나누어 떨어지면 소수가 아님
          }
          return true; // 나누어 떨어지지 않으면 소수
      }
  }

• 2부터 num의 제곱근까지의 숫자로 num을 나눠서 나누어 떨어지는지 확인하고, 만약 나누어 떨어지는 수가 있으면 소수가 아니므로 false를 반환
• 나누어 떨어지는 수가 없으면 true를 반환하여 소수임을 표시

하지만 위의 방식으로 진행하면 시간제한에 걸리게 될 것..을 우리는 모두 안다 🥲