167. Two Sum II - Input Array Is Sorted

• python3

📎 Probelm

Given a 1-indexed array of integers numbers that is already sorted in non-decreasing order, find two numbers such that they add up to a specific target number. Let these two numbers be numbers[index1] and numbers[index2] where 1 <= index1 < index2 <= numbers.length.

Return the indices of the two numbers, index1 and index2, added by one as an integer array [index1, index2] of length 2.

The tests are generated such that there is exactly one solution. You may not use the same element twice.

Your solution must use only constant extra space.

Example 1:

Input: numbers = [2,7,11,15], target = 9
Output: [1,2]
Explanation: The sum of 2 and 7 is 9. Therefore, index1 = 1, index2 = 2. We return [1, 2].

Example 2:

Input: numbers = [2,3,4], target = 6
Output: [1,3]
Explanation: The sum of 2 and 4 is 6. Therefore index1 = 1, index2 = 3. We return [1, 3].

Example 3:

Input: numbers = [-1,0], target = -1
Output: [1,2]
Explanation: The sum of -1 and 0 is -1. Therefore index1 = 1, index2 = 2. We return [1, 2].

Constraints:

• 2 <= numbers.length <= 3 * 104
• -1000 <= numbers[i] <= 1000
• numbers is sorted in non-decreasing order.
• -1000 <= target <= 1000
• The tests are generated such that there is exactly one solution.

Pseudocode

1. Initialize two pointers: one at the beginning index and one at the end index.
2. If the sum the elements at these indices is less than the target value, decrement the end index by one.
3. If the sum is greater than the target value, increment the beginning index by one.
4. If the sum equals the target value, return an array containing the indices.

Code

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:

        l, r = 0, len(numbers)-1
        while l < r:
            s = numbers[l] + numbers[r]
            if s == target:
                return [l+1, r+1]
            elif s < target:
                l += 1
            else:
                r -= 1

Result

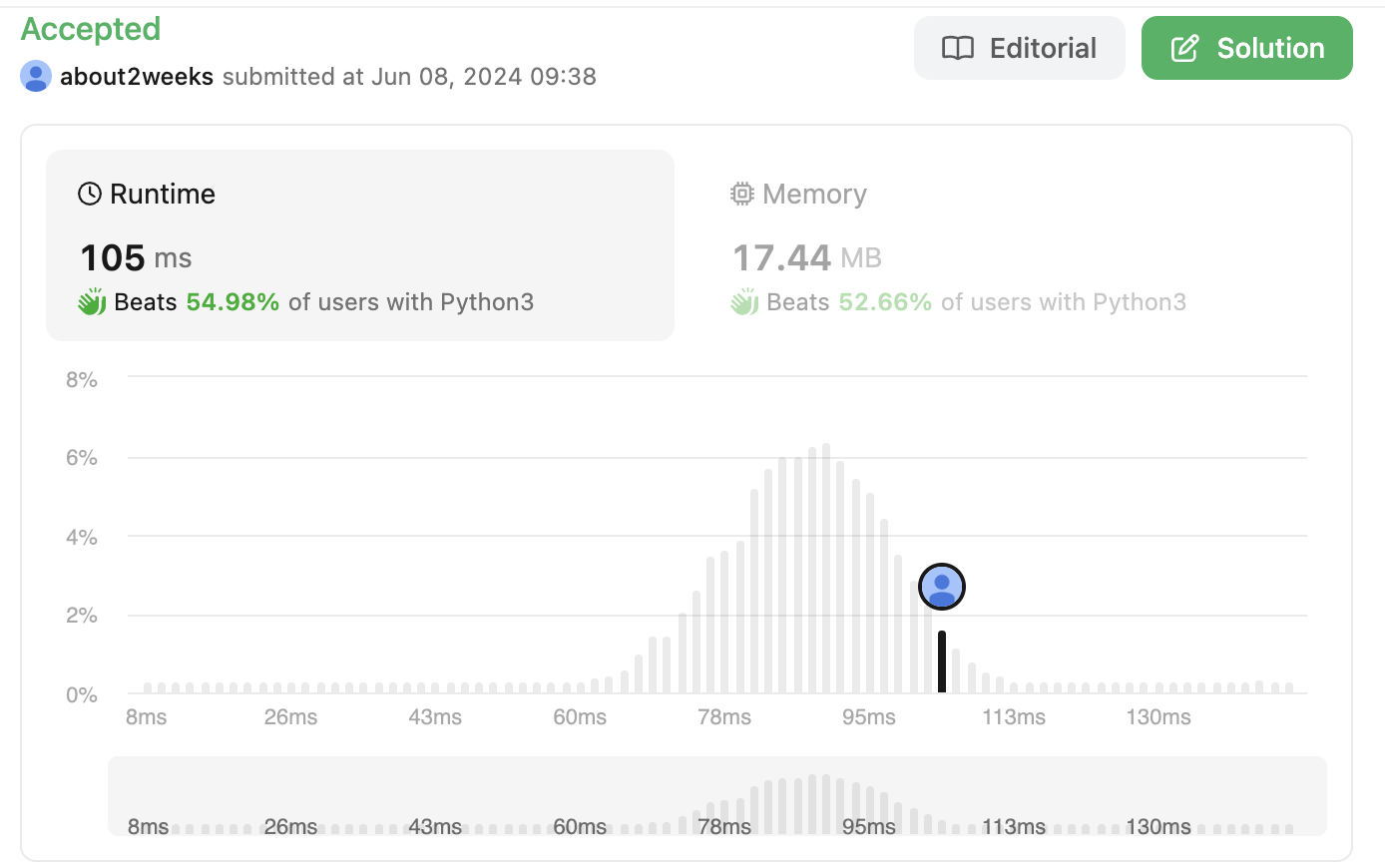
• Time Complexity: O(n)
• Space Complexity: O(1)