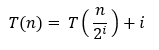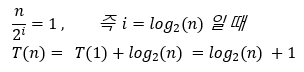시간복잡도
1. 복잡도 카테고리
1) 시간복잡도란?
시간 복잡도란 어떤 알고리즘의 시행 속도를 표현하는 수식을 의미한다.
이 표현 수식의 종류에는 표현 목적에 따라 다음과 같이 총 5가지가 있다
Tight Bound를 구할 때
Big O Notation: 점근적 상한 (Tight Upper Bound)Big Omega Notation: 점근적 하한 (Tight Lower Bound)
Loose Bound를 구할 때
Little O Notation: Loose Upper BoundLittle Omega Notation: Loose Lower Bound
(참고)
(Theta Notation : Big O와 Big Omega가 같을 때 Theta Notation으로 표현할 수 있다.)
2) Big-O Notation 종류
Big-O Notation의 종류는 다음과 같다.
Polynomial Time Complexity
Exponential Time Complexity
참고: 분류 방법
O( f(n) ) 이라고 할 때 f(n)에서 제일 영향이 큰 항을 고른 후 그 계수들을 버리면 위의 카테고리 중 한개를 얻을 수 있다.
우리는 이제부터 f(n)이 아닌 이 카테고리를 통해 해당 알고리즘의 시간복잡도를 표현할 것이다.
3) 증명
위 분류 방법은 상한선(Tight Upper Bound)이 같은 알고리즘들로 나눈 것이라고 볼 수 있다.
즉, 해당 알고리즘들은 최악의 경우에도 해당 시간복잡도보다는 많이 걸리지 않는다는 뜻이다.
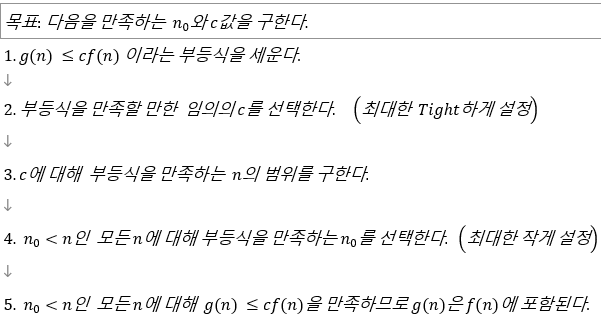
따라서 위의 분류방법은 다음과 같은 순서로 증명할 수 있다.
g(n)의 시간이 걸리는 함수가 있고 f(n)은 위 카테고리중 하나라고 하자.
위의 과정을 마친 후 마지막으로 검토해보는 것도 잊지말자.
(주의할 점)
1. n0를 구할 때 모든 실수에 대해 만족하는 것인지 확인해야 한다.
2. O(n)에는 O(logn)과 같은 복잡도들도 포함된다.
2. 구하는 방법
먼저 입력의 크기에 따라 변하는 부분은 변수 n을 가지고 표현하고 나머지 부분은 통틀어서 1로 표현한다.
그 다음 해당 식을 위의 방법대로 해석하면 된다.
1) 반복문의 시간복잡도

1. 데이터의 크기에 따라 변하는 for문에 대해서만 계산한다.
위의 example은 다음과 같이 표현할 수 있다.
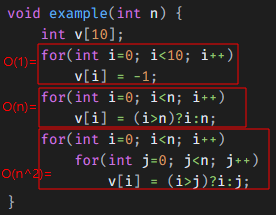
즉, O( T(n) ) = O( n^2 + n + 1) = O(n^2)
2) 재귀함수의 시간복잡도

1. 재귀함수를 점화식으로 표현한다.
위의 BinarySearch는 다음과 같이 표현할 수 있다.

(참고)
-if문 이므로 밑의 T(n/2)는 둘 중 하나만 실행된다.
즉, T(n) = T(n/2) + 1
(만약 case문이었다면 T(n/2)는 둘 다 실행되어 점화식이 바뀐다.)
2-1. 점화식으로 부터 직접 구한다
위의 Binary Search함수를 예시로 시간복잡도를 풀어보자.
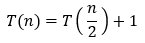
- 전개
먼저 일반항을 찾기 위해 원래 식을 위와 같이 전개한다.
- 일반화
위에서 전개한 식을 통해 T(n)의 일반항을 찾는다.
- T(1)구하기
위의 일반항에서 T(1)일때를 찾아 T(n)을 다시 표현한다.
(이 때, T(1) 은 1로 여기자)
- Big O Notation 구하기
위에서 구한 T(n)을 Big-O Notation으로 표현한다.
2-2. Master Theorem을 적용한다
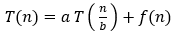
위 점화식이 다음과 같은 조건을 만족한다고 할 때 사용 가능하다.

(참고로 f(n)이 진동하는 함수이면 4번을 절대 만족할 수 없다.)
(즉, T(n) = T(n-1) + 1와 같은 식은 마스터이론을 적용할 수 없다.)
이 때 T(n)의 시간복잡도는 다음과 같다.

여기서 크고 작음의 의미는 함수의 무겁고 가벼움을 의미한다.
2-3. Advanced Master Theorem을 적용한다.
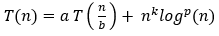
Advanced Master Theorem을 적용하기 위한 조건은 Master Theorem의 조건과 같다.
이 때 T(n)의 시간복잡도는 다음과 같다.