(자료구조) 1. 알고리즘 분석

Ui Jin·2021년 11월 11일
0

자료구조

목록 보기
1/9

개요

만약 두 코드가 같은일을 하고, 이 두 코드를 진행할 때 오류가 발생하지 않는다고 가정해 봅시다.

그렇다면 이중 어떤 코드가 좋은 코드다라는 것은 어떻게 알 수 있을까요?

당연히 더 빠르게 작동하고, 컴퓨터의 자원을 덜 소모하는 코드가 좋은 코드일 것입니다.

또한, 모든 프로그램은 같은 조건에서 동작하는 것이 아니고, 해당 프로그램에 주어진 상황은 항상 달라집니다. 즉, 좋은 코드라고 하더라도 특정 상황에서는 나쁜 코드가 될 수도 있다는 것입니다.

따라서, 좋은 코드란 최악의 상황에서도 최적의 결과를 낼 수 있는 코드여야 합니다.

이러한 프로그램을 만들기 전, 우선 이런 관점으로 코드를 분석하는 방법을 알아봅시다.

알고리즘의 분석방법

(Analysis of Algorithms)

1) Pseudo-code

Pseudo-code란?

알고리즘, 즉 해당 코드의 동작 과정을 설명하는 Code입니다.

사람에게 설명하는 것이 주된 목표이기 때문에 C++보다는 덜 Detail하다고 볼 수 있습니다.

이 Pseudo-code를 보고서 다음의 Primitive operation의 수를 세어보면 해당 코드가 얼마나 빨리 진행되는지 파악할 수 있습니다.

Primitive operations

Primitive operation에는 다음이 있습니다.

  • 사칙연산
  • 대입연산
  • 접근([])
  • 함수호출
  • 함수리턴

즉, 컴퓨터의 작업 과정을 위의 5개의 카테고리로 분류하고 해당 작업을 얼마나 하는지 파악해보는 것입니다.

2) Recurrence Rotation, 재현식

사실 위와 같이 Primitive operations를 하나씩 세는 것은 너무 주먹구구식의 방법이 됩니다.

또한, 코드가 매우 길어질 경우에는 이러한 방법은 거의 불가능할 것입니다.

Asymptotic Analysis

(= Big-Picture Approach)

점근적 분석은 이러한 문제에 대해 해결책을 제시해 줄 수 있습니다. 이 분석 방법은 알고리즘을 분석할 때, primitive operation의 모든 개수가 아닌 그 Growth Rate를 분석하는 것입니다.

이때 Growth Rate는 결국 N이 커질수록 constant factors와 lower-Order term 에는 영향을 받지 않게 됩니다.

(참고)
( N이란 프로그램에게 주어진 상황의 크기라고 생각하면 될 것 같습니다. 예를들어 N개의 수를 분류하는 프로그램과 같이 말이죠! )

이를 활용한 대표적인 방법이 아래의 Big-Oh Notation이 되겠습니다.

Big-Oh Notation

Asymptotic Analysis를 통해서 구할 수 있는 Growth Rate는 대표적으로 다음과 같이 7 Category중의 하나( O(g(n)) )에 해당되게 됩니다.

  • O(n!)
  • O(2n)
  • O(nd)
  • O(n*log n)
  • O(n)
  • O(log n)
  • O(log(log n))
  • O(1)

즉 다시말해서, 우리가 실제로 구한 시간/공간 복잡도 함수가 f(n)이라고 하고 위의 7개중 1개를 g(n)이라고 해봅시다.

이때, f(n) = O(g(n)) 이 성립 된다는 것입니다.

이를 증명하기 위해서는 다음이 성립하는 C와 n0을 찾을수 있음을 보이면 되겠습니다.

f(n) ≤ cg(n) 이다. (단, n에 대해서 n ≥ n0이 성립할 때)

이 식은 g(n) ≤ f(n) ≤ cg(n)이 결국 성립함을 표현함으로써, 복잡도함수 f(n)이 g(n)에 포함됨을 알려줍니다.

(참고)
( g(n)은 f(n)의 Asymtotic upper bound가 된다.)

이 과정을 규칙으로 만들어 보면

  1. f(n)과 g(n)의 식 찾기

  2. f(n) ≤ cg(n)를 만족하는 c값 찾기 (다양한 수가 나올 수 있음)

  3. 이때의 n0 찾기 (c의 값에 따라서 달라짐)

  4. c와 n0를 넣고 다시 증명하기

위와 같이 만들어 볼 수 있겠죠?!
1. 숙지하기

(주의)
(위의 3번과정을 자세히 봐봅시다! 특정 범위에서는 우리가 목표한 결과와 다르다는 것을 기억하고, 우리의 목표는 궁극적(n->∞일 때)인 결과를 얻는 것입니다.)

(예시)
f(n) = 3log n + log(log n)

  1. f(n) g(n) 찾기
    -> g(n) = log n
  1. f(n) ≤ cg(n)
    -> c = 4라고 하자. 즉, 3log n + log(log n) ≤ 4log n
  1. 이때의 n0 찾기
    -> 이때 n3log n ≤ n4 즉, log n ≤ n
    n0 = 1 이라고 하자.
  1. 증명(빼먹지 말자)
    f(n) ≤ 4g(n) (단, n에 대해서 n ≥ 1이 성립할 때)

시간복잡도함수

2. 방법 숙지하기

그렇다면 위의 복잡도함수 f(n)을 어떻게 구하면 될까요?

여기에 대한 규칙을 따로 정해봅시다!

  1. 입력의 크기를 n이라고 하자

  2. 해당 함수 LinearSum의 시간 복잡도 함수를 Tn라고 하자

  3. n과는 관련없는 코드를 통틀어서 1이라고 하자

이것을 다음과 같은 코드에서 살펴보고 이해해 봅시다

1번
다음과 같은 Pseudo-code가 있다.

Algorithm LinearSum(A, n)
    input: An integer array A and an integer n
    output: The sum of the first n integers in A

    if n=1 then
        return A[0]
    else 
        return LinearSum(A, n-1) + A[n-1]
  • 위의 경우 Tn = Tn-1 + 1라고 할 수 있다.
  • 따라서 Tn = n-1 + T1 = n 이라고 할 수 있다
  • 즉, T는 O(n)의 시간 복잡도를 가진다고 할 수 있다.

2번
다음과 같은 Pseudo-code가 있다.

Algorithm power(x, n)
    Input: A number x and an integer n >= 0
    Output: The value x^n

    if n = 0 then
        return 1.0
    if n is odd then
        y <- power(x, (n-1)/2)
        return x*y*y
    else 
        y <- power(x, n/2)
        return y*y
  • 위의 경우 Tn = 1 + Tn/2 이라고 할 수 있다.
  • 따라서 Tn = 1 + 1 + Tn/4 = ... = i + Tn/2i이다. (n = 2i)
  • Tn = log2 n + T1 = log n + 1 이다.
  • 즉, T는 O(log n)의 시간 복잡도 함수를 가진다.

3번
다음과 같은 Pseudo-code가 있다.

Algorithm LinearFibonacci(k)
    Input: An integer k
    Output: A pair(F_k, F_k-1)

    if k<=1 then
        return (k,0)
    else
        (i, j) <- LinearFibonacci(k-1)
    return (i+j, i)
  • 위의 경우 Tn = Tn-1 + 1라고 할 수 있다.
  • 따라서 Tn = n-1 + T1 = n 이라고 할 수 있다
  • 즉, T는 O(n)의 시간 복잡도를 가진다고 할 수 있다.

4번
다음과 같은 Pseudo-code가 있다.

Algorithm BinarySum(A, i, n)
    Input: An integer array A and integers i and n
    Output: The reversal of the n integers in A starting at index i

    if n = 1 then
        return A[i]
    return BinarySum(A, i, [n/2]) + BinarySum(A, i+[n/2], [n/2])
  • 위의 경우 Tn = 1 + Tn/2 + Tn/2 = 1 + 2Tn/2 이라고 할 수 있다.
  • 따라서 Tn = 1 + 2 + 4Tn/4 = ... = 1 + 2 + ... + 2i-1 + 2iTn/2i이다.
    (n = 2i)
  • Tn = 2i - 1 + 2iTn/2i = n-1 + nT1 = 2n-1
  • 즉, T는 O(n)의 시간 복잡도 함수를 가진다.

5번
다음과 같은 Pseudo-code가 있다.

Algorithm BinaryFibo(k)
    Input: An integer k
    Output: The k th Fibonacci number

    if k <= 1 then
        return k
    else
        return BinaryFibo(k-1) + BinaryFibo(k-2)
  • 위의 경우 Tn = 1 + Tn-1 + Tn-2이라고 할 수 있다.
  • 이때 Tn > 1 + Tn-2 + Tn-2 = 1 + 2Tn-2 이다.

(중요)
(피보나치 수열의 경우 일반적인 방법으로 정리가 불가능하다.)

  • 따라서
    Tn > 1 + 2Tn-2 > 1 + 2 + 4Tn-4 > ... > 1 + 2 + ... + 2i-1 + 2iTn-2i이다.
    (n-2i = 1)
  • Tn > 2i+1-1 = 2(n+1)/2 - 1
  • 즉, T는 O(2n)의 시간 복잡도 함수를 가진다.

공간복잡도함수

공간 복잡도 함수도 시간 복잡도 함수와 같습니다.

다만 메모리가 유지되는 시간이 존재한다는 것을 잊지 말아야합니다.

1번
다음과 같은 코드가 있다.

int fibo2(int n){
    int i, f[MAX_SIZE];
    f[0] = 0;
    if(n>0) {
        f[1] = 1;
        for(i=2; i<=n; i++)
            f[i] = f[i-1] + f[i-2];
    }
    return f[n];
}
  • 공간 복잡도는 Tn = 1이다.
    (입력에 따라서 사용하는 공간이 늘거나 줄거나 하지 않는다.)

2번
다음과 같은 Pseudo-code가 있다.

Algorithm BinarySum(A, i, n)
    Input: An integer array A and integers i and n
    Output: The reversal of the n integers in A starting at index i

    if n = 1 then
        return A[i]
    return BinarySum(A, i, [n/2]) + BinarySum(A, i+[n/2], [n/2])
  • 위의 경우 Tn = 1 + Tn/2 이라고 할 수 있다.

(중요)
위의 경우 BinarySum(A, i, [n/2])코드가 우선 실행되고 난 후 BinarySum(A, i+[n/2], [n/2])코드가 실행되는 것이므로 결국 공간은 Tn/2 만큼 사용하게 됩니다.

  • 따라서 Tn = 1 + 1 + Tn/4 = ... = i + Tn/2i이다. (n = 2i)
  • Tn = log2 n + T1 = log n + 1 이다.
  • 즉, T는 O(log n)의 공간 복잡도 함수를 가진다.

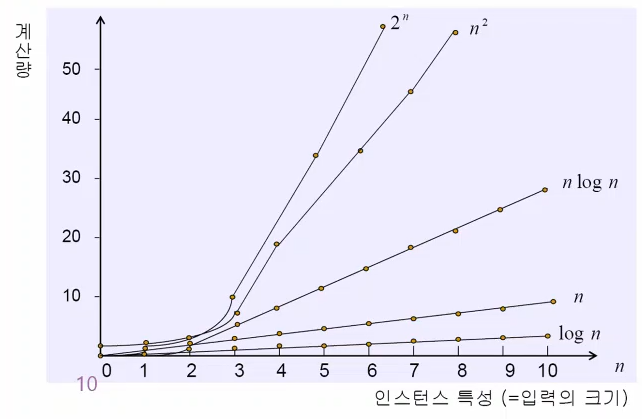
위의 예시들을 살펴보면 해당 7category들의 특징을 파악할 수 있습니다.

  • O(1): Tn = k
    입력의 크기와 상관없이 하는 일이 일정한 알고리즘

  • O(log n): Tn = Tn/2
    다음 턴에서 하는 일이 반씩 줄어드는 알고리즘

  • O(n): Tn = Tn-1
    다음 턴에서 하는 일이 1개씩 줄어드는 알고리즘

  • O(n*log n): Tn = Tn/2 + n
    다음턴에서 하는 일이 반씩 줄어들지만, 이 일들을 n번 더 작업해야 하는 알고리즘

    3. 유도해보기

  • O(2n): Tn = 2Tn-1
    다음 턴에서 하는일이 2배씩 늘어나는 알고리즘

profile
Ui Jin
github로 이전 중... (https://uijinee.github.io/)
다음 포스트

(자료구조) 2. Array와List

0개의 댓글