자 이제 그럼 실제로 앞서 배운 ADT를 어디에 사용할 수 있는지 공부해 봅시다.
Stack Case Study
먼저 Stack부터 살펴 봅시다.
Stack은 그 특성상 주로 history를 이용해야 하는 문제들에서 사용되게 됩니다.
1) Parentheses Matching Algorithm
어떤 문자열에서 괄호가 matching이 잘 되었는지 확인하는 알고리즘을 말합니다.
(참고)
( ): round bracket
{ }: curly bracket, braces
[ ]: square bracket
< >: angle bracket
우선 왜 Stack을 사용하는지부터 생각해 봅시다.
bracket matching이라는 것은 앞에 bracket을 열었을 때, 올바른 위치에서 잘 닫았는지 확인해야 하는 작업을 해야 할 것입니다.
즉, 앞의 정보를 저장해 두고 matching에서 확인하는 작업을 거치면 수월하게 구현할 수 있겠죠
코드 구현 방법 구상
Assume: bracket이 아닌 기호들은 건너 뛰고, 앞에서부터 차례로 검사한다.
1. Opening Symbol을 만나면 Stack에 push()
if((x=='(') || (x=='{') || (x=='[') || (x=='<'))
stack.push(x);2. Closing Symbol을 만나면 Stack에서 pop()
if((x==')') || (x=='}') || (x==']') || (x=='>')) {
if(stack.empty() || (stack.top()!=matching(x)))
return false;
stack.pop();
}
//matching은 Opening Symbol로 반환하는 함수Stack의 상단과 비교했을 때
- Opening Symbol과 같은 종류일 때:
pop()- Opening Symbol과 다른 종류일 때: Matching 실패 (비어있을때 포함)
3. 끝까지 검사한 후 Stack이 비어있으면 Matching 성공
if(stack.empty())
return true;
else
return false;Stack에 bracket이 남아있으면 실패
(Pseudo Code)
Algorithm ParenMatch(X, n):
Input: An array X of n tokens, each of which is either a grouping symbol, a variable, an arithmetic operator, or a number
output: true if and only if all the grouping symbols in X match
Let S be an empty stack
for i=0 to n-1 do
if X[i] is an opening grouping symbol then
S.push(X[i])
else if X[i] is a closing grouping symbol then
if S.isEmpty() then
return false {nothing to match with}
if S.pop() does not match the type of X[i] then
return false {wrong type}
else
skip the token
if S.isEmpty() then
return true {every symbol matched}
else
return false {some symbols were never matched}C++ Code
bool ParenMatching(string& target) {
AVStack stack;
for(int i=0; i<target.length(); i++) {
char x = target[i];
if((x=='(') || (x=='{') || (x=='[') || (x=='<'))
stack.push(x);
else if((x==')') || (x=='}') || (x==']') || (x=='>'))
{
if(stack.empty() || (stack.top()==!matching(x)))
return false;
stack.pop();
}
//else continue;
}
if(stack.empty())
return true;
else
return false;
}2. Stock Span Problem
어떤 배열에서 과거(이전)에 자신보다 작거나 같았던 날이 연속되는 기간의 크기를 구하는 알고리즘
코드 구현 방법 구상
마찬가지로 그냥 분석할 경우 for문을 2번사용하여야 할 것입니다. 즉, 시간이 더 걸리겠죠
하지만 우리가 for문을 1번사용하면서, 중간중간에 과거의 정보를 적당히 변형하여 저장해두어 사용한다면 엄청난 시간을 줄일 수 있을 것입니다.
우선 다음의 배열을 준비한다.
- Winner
i번째 반복에서 과거에 자신보다 큰 원소의 index를 저장하는 stack - Result
분석완료한 정보를 보관하기 위한 배열
Assume: 앞의 원소부터 차례대로 다음의 과정(2번부터)을 반복한다.
1. Winner에서 자기보다 작거나 같은 친구들은 모두 pop()
bool done = false;
while(!Winner.empty() || done) {
if(target[Winner.top()] <= target[i])
Winner.pop();
else
done = true;
}
//더이상 승자가 아니기 때문에그 결과 Winner에는 이전 반복에서까지 자기보다 큰 친구의 index만 저장되어 있음
2. Result에 i-Winner.top()을 저장
그 결과 (자신(i) - 이전에 마지막으로 자신보다 컸던 index(Winner.top())
즉, 자신보다 작거나 같았던 날이 연속되는 index수를 구할 수 있음
int h = 0;
if(Winner.empty())
h = -1;
else
h = Winner.top();
Result[i] = i-h;과거에 자신보다 컸던 날이 없을 경우 현재까지 자신이 가장 컸던 것
즉, 다시말해
-1번 index 이후로자신이 가장 컸다는 것이다.
3. 다음번 분석을 위해 Winner에 자신의 index를 저장
Winner.push(i);결과적으로
i-1번째반복 완료시 Winner에는target[i-1]과 같거나 큰 원소가 저장됨즉,
i번째반복 시작시 Winner에는target[i-1]과 같거나 큰 원소가 저장되어 있음
Pseudo Code
Algorithm computeSpan
Input array P of n integers, and an empty stack D
Output array S of n integers, S[i] is the largest interger k such that k<= i+1 and P[j] <= P[i] for j = i-k+1, ..., i
for i <-- 0 to n-1 do
done <-- false
while not(D.isEmpty() or done) do
if P[D.top()] <= P[i] then
D.pop()
else
done <-- true
if D.isEmpty() then
h <-- -1
else
h <-- D.top()
S[i] <-- i-h
D.push(i)
return SC++ Code
int* StockSpan(int* target, int size) {
int* Result = new int[size];
AVStack Winner;
for (int i = 0; i < size; i++) {
bool done = false;
int h = 0;
while (!(Winner.empty() || done)) {
if (target[Winner.top()] <= target[i])
Winner.pop();
else
done = true;
}
if (Winner.empty())
h = -1;
else
h = Winner.top();
Result[i] = i - h;
Winner.push(i);
}
return Result;
}
// 이 copy를 받은 포인터는 나중에 delete 반드시 필요분석
이해하기 힘들 수 있으니 다음의 예시로 i=0부터 다시 생각해 봅시다.
- 준비
Input: P배열, Stack D
Output: S배열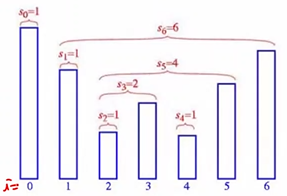
- i = 0일 경우
done = false
D.Empty() = true (D는 아직 비어있음)
--> 즉, while문 작동 X
--> if문 작동 O : h=-1
s[0] = 1, D[0] = 0
결과: s[] = 1, D[] = 0- i = 1일 경우
done = false
D.Empty() = false
--> while문 작동 O
--> P[0] <= P[1]? false : done = true
--> while문 작동 X
--> else문 작동 O : h=0
s[1] = 1, D[1] = 1
결과: s[] = {1, 1} D[] = {0, 1}- i = 2일 경우
done = false
D. Empty() = false
--> while 문 작동 O
--> P[1] <= P[2]? false : done = true
--> while문 작동 x
--> else문 작동 O: h=1
s[2] = 1, D[2] = 2
결과: s[] = {1, 1, 1}, D[] = {0, 1, 2}- i = 3일 경우
done = false
D. Empty() = false
--> while 문 작동 O
--> P[2] <= P[3]? true : D.pop()
--> p[1] <= p[3]? false : done = true
--> while문 작동 x
--> else문 작동 O: h=1
s[3] = 2, D[2] = 3
결과: s[] = {1, 1, 1, 2}, D[] = {0, 1, 3}- i = 4일 경우
done = false
D. Empty() = false
--> while 문 작동 O
--> P[3] <= P[4]? false : done = true
--> while문 작동 x
--> else문 작동 O: h=3
s[4] = 1, D[3] = 4
결과: s[] = {1, 1, 1, 2, 1}, D[] = {0, 1, 3, 4}- i = 5일 경우
done = false
D. Empty() = false
--> while 문 작동 O
--> P[4] <= P[5]? true : D.pop()
--> P[3] <= p[5]? true : D.pop()
--> p[1] <= p[5]? false : done = true
--> while문 작동 x
--> else문 작동 O: h=1
s[5] = 4, D[2] = 5
결과: s[] = {1, 1, 1, 2, 1, 4}, D[] = {0, 1, 5}- i = 6일 경우
done = false
D. Empty() = false
--> while 문 작동 O
--> P[5] <= P[6]? true : D.pop()
--> P[1] <= p[6]? true : D.pop()
--> p[0] <= p[6]? false : done = true
--> while문 작동 x
--> else문 작동 O: h=0
s[6] = 6, D[1] = 6
결과: s[] = {1, 1, 1, 2, 1, 4, 6}, D[] = {0, 6}3. Postfix Notation
중위 표기식을 후위 표기식으로 변환하는 알고리즘을 Stack을 사용해서 구현해 보겠습니다.
(참고)
수식 표기법
1) prefix notation(전위 표기법) : 연산자가 피연산자 앞에 위치
2) infix notation(중위 표기법) : 연산자가 피연산자 가운데 위치
3) postfix notation(후위 표기법) : 연산자가 피연산자 뒤에 위치후위 표기법의 장점
1) 우선 계산전, 컴퓨터는 수식을 어떤 배열에 저장합니다
2) 이때 중위 표기법을 선택할 경우, 배열을 모두 읽고 계산 우선순위를 매겨야 하므로 컴퓨터가 해석하기 불리하게 됩니다.
3) 하지만 후위 표기법은 괄호가 불필요하고 연산 순서가 간단하다후위 표기법 계산 방법(후위표기식->중위표기식)
1) Operand를 만날 경우 그대로 적자.
2) Operator를 만날 경우 그 전에 적어놓았던 OperandA,B로 연산을 수행하고 그 결과C를 적자(예시)
ex1)A+B\*C = ABC\*+
ex2)ABC*+DE/- = {A+(B\*C)} - {D/E}
코드 구현 방법 구상
후위 표기식은 우리에게 생소한 방법입니다. 따라서 다음의 방법으로 진행된 다는 것을 알려드리겠습니다.
중위 표기식->후위표기식
우선 다음의 배열을 준비한다.
-
Oper
operator들을 "잠시"저장하기 위한 Stack -
Result
변환 결과를 저장하기 위한 Stack
assume: 수식을 앞에서 부터 차례대로 읽어가며 다음 규칙대로 행동
1. Operand(피연산자)를 만날 경우 Result에 push()
if(getToken(token)=="Operand")
Result.push(token);2. Operator(연산자)를 만날 경우 Oper에 push()
if(getToken(token)=="Operator") {
while(PIE(token) <= PIS(Oper.top())) {
result.push(Oper.top());
Oper.pop();
}
Oper.push(token);
}이때 다음의 제약 조건을 가진다
Oper.top()의 연산 우선순위가 낮을경우
-> 그대로Oper에push()
Oper.top()의 연산 우선순위가 더 높을 경우
->Oper.top()의 연산 우선순위가 더 낮을 때까지pop()한 후push
-> 이때pop()한 연산자는 바로바로 Result에push()즉, Oper의 Stack은 나중에 들어온 연산의 우선순위가 더 높도록 유지해야 한다.
3. 괄호의 경우 2개의 우선 순위를 갖는다
if(getToken(token)==")"){
while(Oper.top() != "("){
Result.push(Oper.top());
Oper.pop();
}
Oper.pop() //마지막 남은 "("까지 제거
}
- stack에 들어가기 전: 우선순위 가장 높음
stack에 들어간 후: 우선순위 가장 낮음즉,
(는 제약조건 없이 항상 Oper에 들어가고 바로 후에 들어오는 연산자 또한 제약조건 없이 항상 Oper에 들어가게 됨단,
)를 만날 경우(가 나올 때 까지pop()해야 함
4. 수식이 끝나면 Oper에 존재하는 연산자들을 옮긴다
if(getToken(token)==NULL){
while(!Oper.empty()){
Result.push(Oper.top());
Oper.pop();
}
}C++ Code
void postfix(string& infix) {
AVStack Oper;
AVStack Result;
for(int i=0; i<infix.length(); i++) {
int token = getToken(infix[i]);
switch(token){
case 1: // OPERAND:
Result.push(token);
break;
case 2: // OPERATOR
while(PIS(Oper.top()) >= PIE(token)) //Stack안의 우선순위와 밖의 우선순위는 다르다.
{
Result.push(Oper.top());
Oper.pop();
}
Oper.push(token);
break;
case 3: // ')'일 경우
while(Oper.top() != '(') {
Result.push(Oper.top());
Oper.pop();
}
Oper.pop(); // '('제거
break;
case 4: // NULL일 경우
while(!Oper.empty()) {
Result.push(Oper.top());
Oper.pop();
}
break;
}
}
cout << Result << endl;
}getToken()함수: OPERATOR, OPERAND, ")", NULL을 반환하는 함수PIS()함수: Stack내의 연산자 우선순위를 반환하는 함수PIE()함수: 연산자의 우선순위를 반환하는 함수
