Stack ADT
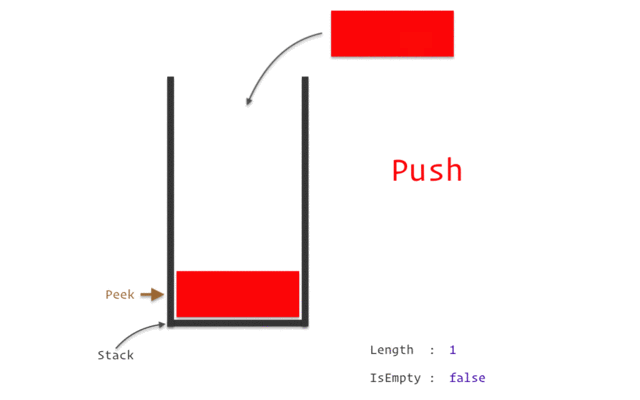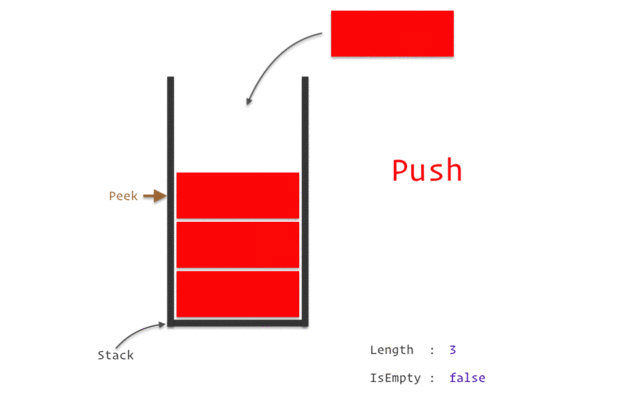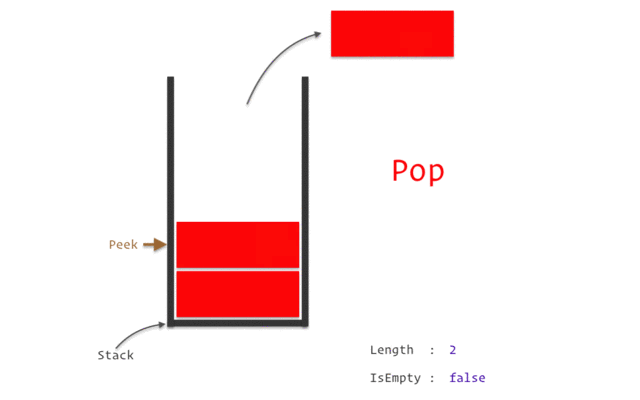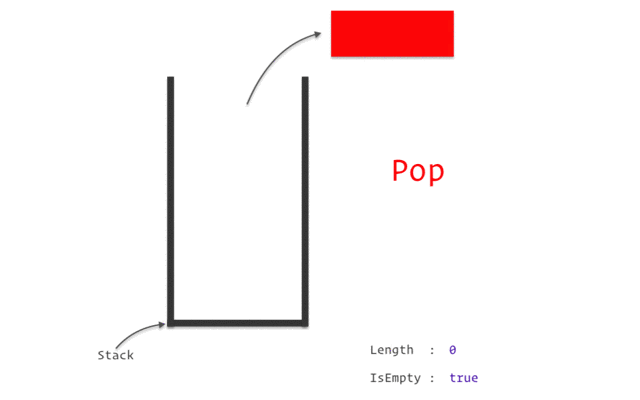
Stack은 LIFO(Last-In First-Out)의 특성을 같는 저장 공간을 의미합니다.
이것은 프링글스 통으로 많이들 비유하는데요, 한쪽이 막혀있는 프링글스 통에 물건들을 집어 넣는다고 생각해 봅시다.
이때 이 물건들을 꺼낸다고 할 때 당연히 가장 위에 있는 것들을 먼저 꺼내야만 할 것입니다.
Main Operation
위의 정의로부터 다음의 함수는 Stack에 반드시 존재해야 함을 알 수 있습니다.
-
push()
Stack의 맨 위에 push()안의 값을 추가하는 함수입니다. -
pop()
Stack의 맨 위의 값을 제거하는 함수입니다.
Auxiliary Operation
위의 함수 외에도 다음과 같은 함수가 존재할 수 있을 것입니다.
-
size()
Stack이 얼마나 차 있는지 알 수 있는 함수입니다. -
isEmpty()
Stack이 비어있는지 확인하는 함수입니다. -
top()
Stack의 맨 위의 값을 return 하는 함수입니다.
Pros & Cons
장점
-
공간 복잡도함수는 O(n)이다
-
Stack의 기능을 수 행하는 각 함수의 시간 복잡도는 O(1)이다.
단점(한계)
- a Priori
우리가 사용할 Stack의 크기를 미리 아는것이 불가능하다. 즉 쓸데 없는 공간의 낭비가 생길 수 있다.
해결방법
1) Array를 이용해 구현한 후 Full Exception을 일으키면 크기를 doubling해준다.2) linked list를 이용하여 해결한다.
구현
ArrayVector로 구현하기
stack은 한쪽에서만 push()와 pop()이 일어나는 자료구조이다.
따라서 stack을 구현할 때에는 우선 앞쪽과 뒤쪽중 어디에서 push()와 pop()을 할지 결정하는게 중요하다.
ArrayVector
먼저번에 구현했었던 ArrayVector를 이용하면 좀 더 쉽게 구현할 수 있을 것이다
class ArrayVector {
public:
ArrayVector();
~ArrayVector();
ArrayVector(ArrayVector& Arr);
ArrayVector& operator=(ArrayVector& Arr);
Elem& operator[](int i){ if (i <= Size) return A[i]; }
void reserve(int N);
void insert(int i, const Elem& e);
void erase(int i);
int size() const { return Size; }
int GetCapacity() const { return capacity; }
bool empty() const { return Size == 0; }
friend ostream& operator<<(ostream& out, ArrayVector& Arr);
private:
int capacity;
int Size;
Elem* A;
};
inline ostream& operator<<(ostream& out, ArrayVector& Arr) {
int i;
out << "(";
for (i = 0; i < Arr.size() - 1; i++)
out << Arr[i] << ", ";
out << Arr[i] << ")" << endl;
return out;
}ArrayVector::ArrayVector()
:capacity(0), Size(0), A(NULL)
{ }
ArrayVector::~ArrayVector() {
delete[] A;
}
ArrayVector::ArrayVector(ArrayVector& Arr) {
capacity = Arr.GetCapacity();
Size = Arr.size();
A = new Elem[capacity];
for (int i = 0; i < Size; i++) {
A[i] = Arr[i];
}
}
ArrayVector& ArrayVector::operator=(ArrayVector& Arr) {
if (this != &Arr) {
delete[] A;
capacity = Arr.GetCapacity();
Size = Arr.size();
A = new Elem[capacity];
for (int i = 0; i < Size; i++) {
A[i] = Arr[i];
}
}
return *this;
}
void ArrayVector::reserve(int N) {
if (capacity >= N) return;
Elem* B = new Elem[N];
for (int j = 0; j < Size; j++)
B[j] = A[j];
if (A != NULL) delete[] A;
A = B;
capacity = N;
}
// 저장공간을 설정하는 함수
// 1. 입력값이 현재 용량보다 작으면 실행X
// 2. 입력받은 값으로 새로 동적할당 실행
// 3. 원래 A는 지우고 새로 동적할당한 배열을 다시 A가 가리키도록 함
void ArrayVector::insert(int i, const Elem& e) {
if (Size >= capacity)
reserve(max(1, 2 * capacity));
for (int j = Size - 1; j >= i; j--)
A[j + 1] = A[j];
A[i] = e;
Size++;
}
// i번째에 원소를 집어넣는 함수
// 1. 저장공간이 알맞는지 판단
// 2. 저장공간이 가득찬 경우 2배 (max(1, 2*capacity))
// 3. 한칸씩 미루고 그 자리에 삽입
void ArrayVector::erase(int i) {
for (int j = i + 1; j < Size; j++)
A[j - 1] = A[j];
Size--;
}
// i번째 원소를 삭제하는 함수
// 1. i+1부터 한칸씩 앞으로 당겨 i번째 원소 삭제ArrayVectorStack
위의 ArrrayVector의 특성을 활용해서 Stack처럼 작동하도록 구현해 보자.
아래의 코드를 보면 알겠지만 ArrayVector에 복사생성자 같은 기능들이 구현되어 있기 때문에 훨씬 간단해 진다.
class AVStack {
public:
AVStack();
~AVStack();
AVStack(AVStack& s);
AVStack& operator=(AVStack& s);
void push(const Elem& e) { Arr.insert(0, e); }
void pop() { if (!empty()) Arr.erase(0); }
int size() const { return Arr.size(); }
bool empty() const { return Arr.empty(); }
const Elem& top() { if (!empty()) return Arr[0]; }
friend ostream& operator<<(ostream& out, AVStack& s);
protected:
ArrayVector& GetArray() { return Arr; }
private:
ArrayVector Arr;
};
inline ostream& operator<<(ostream& out, AVStack& s) {
out << s.GetArray();
return out;
}AVStack::AVStack()
: Arr()
{ }
AVStack::~AVStack()
{ }
AVStack::AVStack(AVStack& s)
: Arr(s.GetArray())
{ }
AVStack& AVStack::operator=(AVStack& s) {
Arr = s.GetArray();
return *this;
}List로 구현하기
stack은 한쪽에서만 push()와 pop()이 일어나는 자료구조이다.
따라서 마찬가지로 stack을 구현할 때에는 우선 앞쪽과 뒤쪽중 어디에서 push()와 pop()을 할지 결정하는게 중요하다.
Singly Linked List로 구현하기
위의 구현중에서 push()와 pop()을 어떤 방식으로 구현할 것인지 정하였으면 이제 실제로 Stack을 구현해 볼 수 있을 것이다.
여기서는 Singly Linked List의 단점을 고려해서 head부분에서 push()와 pop()을 수행하기로 결정하였다.
Node를 정의
struct Node {
Node() { };
Node(const Elem& e, Node* n)
:elem(e), next(n)
{ }
Elem elem;
Node* next;
};Stack의 특성에 맞게 Node를 연결하기
class SLStack {
public:
SLStack();
~SLStack();
SLStack(const SLStack& s);
SLStack& operator=(const SLStack& s);
void push(const Elem& e);
void pop();
int size() const { return Size; }
bool empty() const { return Size == 0; }
const Elem& top() const { return head->elem; }
friend ostream& operator<<(ostream& out, SLStack& target);
protected:
Node* GetHead() const { return head; }
void CopyFrom(const SLStack& origin);
private:
Node* head;
Node* tail;
int Size;
};
inline ostream& operator<<(ostream& out, SLStack& target) {
Node* temp = target.GetHead();
while(temp != NULL){
out << temp->elem;
temp = temp->next;
}
return out;
}
SLStack::SLStack()
:Size(0), head(NULL), tail(NULL)
{ }
SLStack::~SLStack() {
while (!empty())
pop();
}
SLStack::SLStack(const SLStack& s) {
CopyFrom(s);
}
// 원래 비어있어 바로 CopyFrom()사용 가능
SLStack& SLStack::operator=(const SLStack& s) {
if (this != &s) {
while (!empty())
pop();
CopyFrom(s);
}
return *this;
}
// if(this!=&s): 자기할당을 피해야 함!!
// CopyFrom()은 빈 stack만 사용 가능
void SLStack::CopyFrom(const SLStack& origin) {
head = NULL;
Node* CopyTo = head;
Node* CopyFrom = origin.GetHead();
while (CopyFrom != NULL) {
Node* v = new Node(CopyFrom->elem, NULL);
if (CopyTo == NULL)
head = v;
else
CopyTo->next = v;
CopyTo = v;
CopyFrom = CopyFrom->next;
}
tail = CopyTo;
Size = origin.size();
}
// - protected처리
// CopyFrom()의 경우 빈 stack만 사용 가능
// - 연결
// 1. elem을 가지고 Null을 가리키는 새로운 Node를 만듬
// 2. 새로 만든 stack을 차례대로 연결
// 2-1. origin stack의 현재원소(CopyFrom)를 가리키는 포인터 이용
// 2-2. 새로 만든 stack의 원소(CopyTo)를 가리키는 포인터 이용
void SLStack::push(const Elem& e) {
Node* temp = new Node(e, NULL);
if (Size == 0)
tail = temp;
else
temp->next = head;
head = temp;
Size++;
}
// Head를 pop()하는 Stack은 Head에서 push()가 일어나야 함
// Size가 0일경우 head와 tail은 같은 곳을 가리킴
void SLStack::pop() {
if (Size > 0) {
Node* temp = head;
head = temp->next;
delete temp;
Size--;
}
}
// List의 Head를 pop()하는 형식의 Stack이다.
// Singly Linked List는 Tail의 prev에 접근하기 까지 시간이 걸리기 때문Doubly Linked List
마찬가지로 위에서 어떤 방법으로 push()와 pop()을 수행할 것인지 먼저 정한후에 실제로 Stack을 구현해보도록 하자.
Doubly는 Singly와 다르게 어느 쪽을 선택해도 상관없다. 따라서 여기서는 trailer부분에서 push()와 pop()을 수행하도록 해보자.
Node를 정의
struct Node {
Node() { };
Node(const Elem& e, Node* p, Node* n)
:elem(e), prev(p), next(n)
{ }
Elem elem;
Node* prev;
Node* next;
};Stack의 특성에 맞게 Node를 연결하기
class DLStack {
public:
DLStack();
~DLStack();
DLStack(const DLStack& s);
DLStack& operator=(const DLStack& s);
void push(const Elem& e);
void pop();
int size() const{ return Size; }
bool empty() const { return Size == 0; }
const Elem& top() const { return trailer->prev->elem; }
friend ostream& operator<<(ostream& out, DLStack& target);
protected:
Node* GetHeader() const { return header; }
Node* GetTrailer() const { return trailer; }
void CopyFrom(const DLStack& origin);
private:
Node* header;
Node* trailer;
int Size;
};
inline ostream& operator<<(ostream& out, DLStack& target){
Node* temp = target.GetHeader()->next;
while(temp != target.GetTrailer()){
out << temp->elem;
temp = temp->next;
}
return out;
};
DLStack::DLStack() {
header = new Node();
trailer = new Node();
header->next = trailer;
trailer->prev = header;
Size = 0;
}
// Doubly Linked List의 경우 Sentinel Node가 필요하다.
// 따라서 header와 trailer가 가리키는 Node는 Stack 생성시에 바로 결정된다.
// (header와 trailer가 가리키는 Node는 push()나 pop()에 관계없이 항상 같음)
DLStack::~DLStack() {
while (!empty())
pop();
delete header;
delete trailer;
}
// 마지막에 Sentinel Node도 delete해주어야 하는 것을 잊지말자.
DLStack::DLStack(const DLStack& s) {
CopyFrom(s);
}
// 원래(sentinel까지) 비어있어 바로 CopyFrom()사용 가능
DLStack& DLStack::operator=(const DLStack& s) {
if (this != &s) {
while (!empty())
pop();
delete header;
delete trailer;
CopyFrom(s);
}
return *this;
}
// if(this!=&s): 자기할당을 피해야 함!!
// CopyFrom()은 sentinel까지 빈 stack만 사용 가능
void DLStack::CopyFrom(const DLStack& origin) {
header = new Node();
trailer = new Node();
Node* CopyTo = header;
Node* CopyFrom = origin.GetHeader()->next;
while (CopyFrom != origin.GetTrailer()) {
Node* v = new Node(CopyFrom->elem, NULL, NULL);
CopyTo->next = v;
v->prev = CopyTo;
CopyTo = v;
CopyFrom = CopyFrom->next;
}
CopyTo->next = trailer;
trailer->prev = CopyTo;
Size = origin.size();
}
// - protected처리
// CopyFrom()의 경우 빈 stack만 사용 가능 (sentinel까지 빈)
// - 연결
// 1. Singly와는 다르게 header는 NULL이 아닌 Sentinel Node를 가리키고 있음
// 2. elem을 가지고 Null을 가리키는 새로운 Node를 만듬
// 3. 새로 만든 stack을 차례대로 연결
// 3-1. origin stack의 현재원소(origin)를 가리키는 포인터 이용
// 3-2. 새로 만든 stack의 원소(copy)를 가리키는 포인터 이용
void DLStack::push(const Elem& e) {
Node* temp = new Node(e, NULL, NULL);
temp->prev = trailer->prev;
temp->next = trailer;
trailer->prev->next = temp;
trailer->prev = temp;
Size++;
}
// trailer에서 pop()하는 Stack은 trailer에서 push()가 일어나야 함
void SLStack::pop() {
if(Size>0) {
Node* temp = trailer->prev;
temp->prev->next = trailer;
trailer->prev = temp->prev;
delete temp;
Size--;
}
}
// List의 trailer->prev를 pop()하는 형식의 Stack이다.