자료구조의 종류
Sequential Data Structure()
Hierarchical Data Structure(계층구조)

Root Node: 부모가 없는 Node
Leaf Node(External Node): 자식이 없는 Node
Internal Node: 자식이 하나라도 있는 Node

Parent: Child의 바로 위에 연결되어 있는 Node
Child: 부모의 아래에 바로 연결되어 있는 Node
Sibling: 형제Node

Depth of a Node: Ancestors의 수(Node의 속성)
(Root의 Depth는 0이고 아래 자식으로 갈수록 1씩 증가함)

Height of a Tree: Depth의 최댓값(Tree의 속성)

Degree(fanout, order): 자식의 수

Traversal
접근은 항상 Root에서부터 시작, 하지만 방문순서가 다름.

• Preorder(전위순행)
  Parent -> Left Child -> Right Child

PreOrder(v){
    visit(v)
    for each child w of v
        PreOrder(w)
}

• Inorder(중위순행)
  Left Child -> Parent -> Right Child

InOrder(v){
    if isInternal(v)
        InOrder(leftChild(v))
    visit(v)
    if isInternal(v)
        InOrder(rightChild(v))
    
    // degree가 2개 이상일 경우
    // visit(v)
    // if isInternal(v)
    //    InOrder(rightChild(v)) ...를 계속 이어붙임
    // 결과적으로 v는 degree-1번 방문함
}

(참고)
중위표기식에 대한 Tree를 Inorder로 방문하면 중위 표기식이 된다.

predecessor 와 successor
어떤 요소를 Inorder로 n번째 방문했다고 하면
n-1번째로 방문했던 요소를 predecessor라고 하고
n+1번째로 방문했던 요소를 successor라고 한다.

• Postorder(후위순행)
  Left Child -> Right Child -> Parent

PostOrder(v){
    for each child w of v
        PostOrder(w)
    visit(v)
}

(참고)
중위표기식에 대한 Tree를 Postorder로 방문하면 후위 표기식이 된다.

tip
이 방문 순서는 어느 SubTree에서 보던지 간에 일정해야함.
-> 이 사실로 검산 가능

참고
euler traversal
방문을 처음 중간 끝 모두하는 것

종류

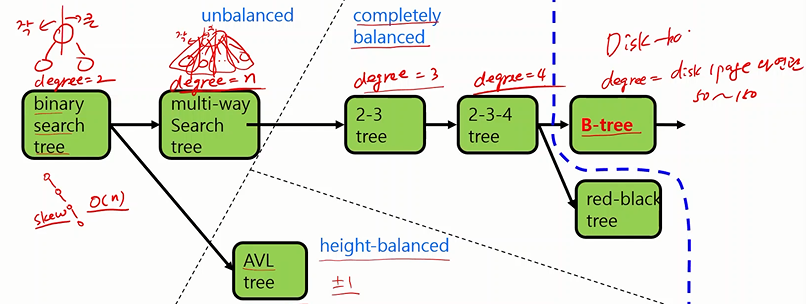
Binary Tree(BT)

이진 트리

Binary Search Tree(BST)

이진트리 + 조건

조건
key(left) <= key(parent) <= key(right)

장점
조건에 의해 탐색속도가 매우 빠름

구현

Binary Tree

Array로 구현

Binary Tree일 경우
왼쪽 = 2depth
오른쪽 = 2depth+1

list로 구현

    struct Node{
        Elem elem;
        Node* parent;
        Node* left;
        Node* right
        
        Node()
            :parent(NULL), left(NULL), right(NULL)
        { }
        Node* sibling() const{
            return (this==parent->left ? parent->right: parent->left);
        }
    }

class LinkedBinaryTree{
public:
    Node* root() { return Root; }
    Node* LeftChild(Node* v) const { return v->left; }
    Node* RightChild(Node* v) const { return v->right; }
    
    void SetRoot(Node* r){
        Root = r;
        r->parent = NULL;
    }
    void ReplaceElement(Node* n, const Elem& e){
        n->elem = e;
    }
    void ExpandExternal(Node* n, Elem left, Elem right){
        n->left = new Node;
        n->right = new Node;
        
        n->left->parent = n;
        n->left->elem = left;
        n->right->parent = nl
        n->right->elem = right;
    }
    
    void RemoveExternal_And_Above(Node* n) {
        Node* p = n->parent;
        Node* s = n->sibling();
        if(IsRoot(p) SetRoot(s);
        else{
            Node* g = p->parent;
            if(p==g->left)
                g->left = s;
            else
                g->right = s;
            s->parent = g;
        }
        delete n;
        delete p;
        size -= 2;
    }
    
    bool IsExternal(Node* n) const { return (n->left==NULL)&&(n->right==NULL)}
    bool IsInternal(Node* n) const { return !IsExternal(n); }
    bool IsRoot(Node* n) const { return (n==Root); }
private:
    Node* Root;
    int size;
};

Binary Search Tree

중요
Binary Search Tree에서는 어떤 Node의 predecessor는 해당 Node보다 바로 작은 값이 저장되어 있고 successor에는 바로 큰 값이 저장되어 있음

list로 구현

삽입과정
1. 들어갈 자리 find
2. external일 경우: 그냥 삽입
internal일 경우: (오른쪽/왼쪽)child로 이동해 다시 find후 삽입

Position find(const key& k){
    BTPosition p = finder(k, T.root());
}
BTPosition finder(const key& k, const BTPostion& p){
    if(T.IsExternal(p))
        return p;
    key curkey = key(p);
    if(k<curkey)
        return finder(k, T.leftChild(p));
    else if(k>curkey)
        return finder(k, T.rightChild(p));
    else
        return p;
}
void insert(const key& k, const Elem& e){
    inserter(k, e);
}

BTPostion Inserter(const key& k, const Elem& e){
    BTPostion p = finder(k, T.root());
    while(T.IsInternal(p))
        p = finder(k, T.rightchild(p)); // 오른쪽에서 자리를 다시 찾음
    T.expandExternal(p);
    setItemp(p, BSTItem(k, e));
    return p;
}
// 중요
// 삽입할 자리가 External일 경우: 자리에 맞게 삽입
// 삽입할 자리가 Internal일 경우: 자리를 다시 찾아야 함
// (오른쪽에서 찾을지 왼쪽에서 찾을지 결정)

삭제과정
1. 삭제할 자리 find
2. external일 경우: remove external_and_above()실행
internal일 경우: 삭제할 요소의 predecessor나 Successor를 찾아 바꾼 후에
remove external_and_aboce()실행

void Remove(const key& k, const Elem& e){
    BTPostion p = finder(k, T.root());
    remover(p);
}

BTPostion Remover(const BTPostion& r){
    BTPostion p;
    if(T.isExternal(T.leftChild(r))
        p=T.leftchild(r);
    else if (T.isExternal(T.rightChild(r))
        p=T.rightchild(r);
    
    // child가 external일 경우 child를 그냥 삭제
    
    else {
        p=T.rightchild(r);
        do
            p=T.leftchild(p);
        while(T.isInternal(p));
        setItem(r, T.parent(p).element()); // 찾은 값을 대입한 후 해당 찾은값의 external Node 삭제
    }
    T.removeExternal_AND_Above(p)
}
// 중요
// 삭제할 자리가 External일 경우: 자리에 맞게 삭제
// 삭제할 자리가 Internal일 경우: 자리를 다시 찾아야 함


// successor찾는 팁: rightchild로 옮긴 후 NULL이 나올 때 까지 leftchild로 옮겨감.
// predecessor찾는 팁: leftchild로 옮긴 후 NULL이 나올 때 까지 rightchild로 옮겨감

2-3 Tree

조건

1) binary Search Tree

2) node에는 최대 2개의 데이터 값이 존재할 수 있음

3) Leaf node를 제외한 node의 degree는 2또는 3어야 함

4) 모든 Leaf가 같은 Level에 위치해야 함(balanced tree).

delete

1) leaf node일 때
-> 그냥 지움

2) leaf node가 아닐때
-> left child의 값이 1개일 때: right child의 가장 작은 값으로 대체한다.

-> right child의 값이 1개일 때: left child의 가장 큰 값으로 대체한다.

...

2-4 Tree

B-Tree

조건

1) Leaf Node를 제외한 모든 Node는 2개 이상의 자식 Node를 가진다.

list로 구현

performace

balanced tree
모든 leaf 노드가 같은 level에 있는 tree
-> 최선의 상황

skew tree
모든 노드가 한쪽으로 치우쳐져서 list처럼 되는 것
-> 최악의 상황

• Binary Search Tree의 문제점