이 문제는 반례 하나만 생각하면 쉽다.
틀린풀이
Flow를 처음부터 생각해보자.
목표지점까지 최소로 도달해야한다.
그래프 형태이다.
딱, 여기서부터 BFS를 사용해야겠다, 라는 생각이 들었다.
두번째, 방문처리를 이미 했으면 다시 방문을 안해야한다고 생각했다.
왜냐하면, queue이기 때문에 이미 방문을 한시점이 최소라고 생각했기 때문이다.
그렇다면, 항상 말부터 이동을 먼저하고 그다음 원숭이가 방문하는 형식으로 진행하면 된다고 생각했다.
왜냐하면
0 0 0
0 0 0
에서 2,3을 한번에 말로 이동을 했다고 치자, 그러면
굳이 1,1 1,2 1,3 그다음 2,3확인시 이미 앞에서 2,3을 한번에 이동시킨게 방문처리가 되어있으므로 4번이나 움직여서 간걸 처리를 안해버리면 된다고 생각했기 때문이다.
그러나 문제는 말부터 항상 이동시킨다고 해서 그게 최선의 결과가 항상 나오는게 아니다.
예를들어, K가 1일때
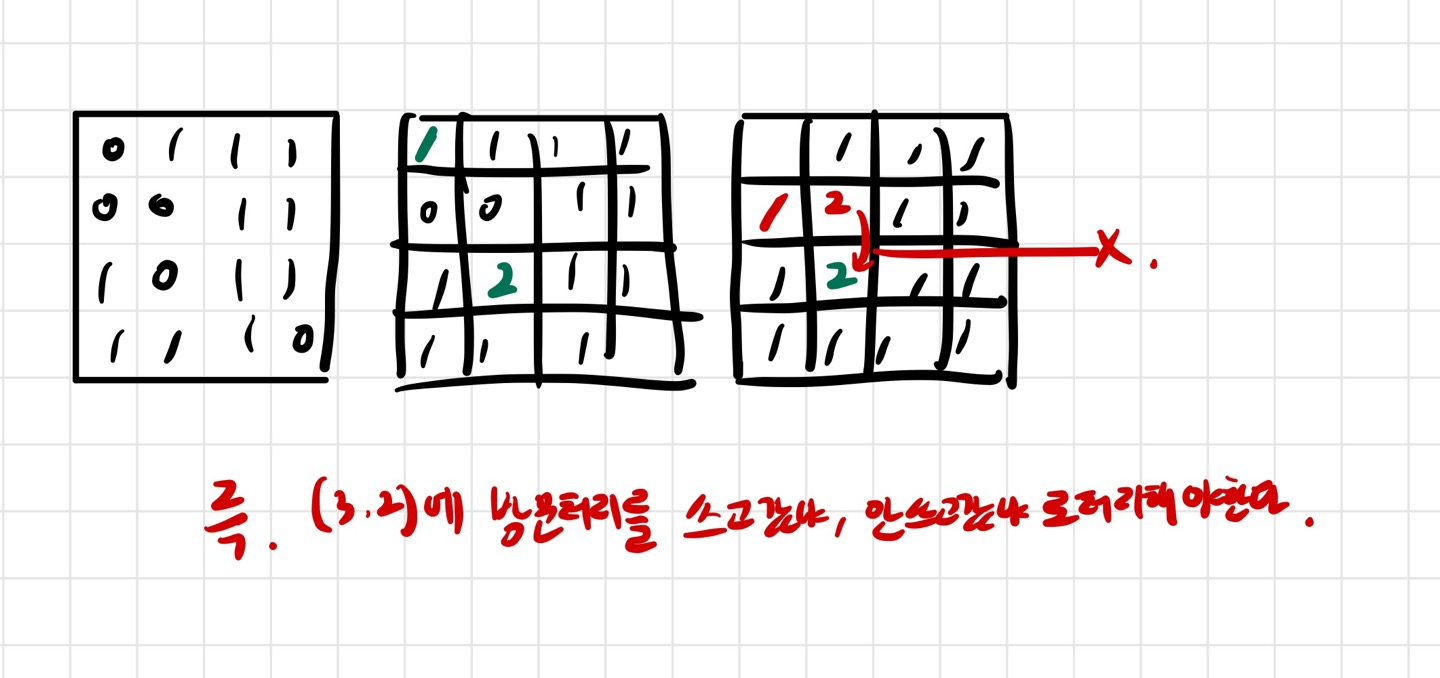
만약 1,1에서 말부터 움직여서 초록색 1,2로 이동했다고 치자. 끝칸까지 가야하는데 이미 점프를 써버려서 도달을 못한다.
그다음에 원숭이로 이동을 하면, 빨간색으로 1,2,그다음에 3,2에 가야하는데, 이미 말이 방문처리를 해버려서 3,2에 방문을 못한다.
아직 점프를 안해서 3,2에 가서 점프를하면 되는데 말이다.
그래서 핵심은 그럼, 아직 뛰지 않은 놈들은 3,2에 방문이 가능해야한다는것이다.
이말은 다르게, 뛴 횟수에 따라 다르게 3,2 방문처리르 해줘야한다는것이다.
이말은 3차원 배열로 처음에 말부터 뛰면 [3][2][1] = true지만
[3][2][0] = false이기 때문에, 한번도 안뛴 놈들은 여기가 false라서 방문처리를 할 수 있게 해야한다.
정답코드
#include <iostream>
#include <queue>
using namespace std;
int K = 0;
int W, H = 0;
int map[201][201] = { 0, };
bool visited[201][201][31] = { false, };
int Answer = 100000000;
int m_dx[4] = { 0,0,1,-1 };
int m_dy[4] = { 1,-1,0,0 };
int h_dx[8] = { -2,-1,-2,-1,1,2,1,2 };
int h_dy[8] = { -1,-2,1,2,2,1,-2,-1 };
void init() {
cin >> K;
cin >> W >> H;
for (int i = 0; i < H; i++) {
for (int j = 0; j < W; j++) {
int tmp = 0;
cin >> tmp;
map[i][j] = tmp;
}
}
}
void bfs() {
queue<pair<pair<int, int>, pair<int, int>>>q;
q.push({ { 0,0 }, { 0, 0 } });
visited[0][0][0] = 1;
while (!q.empty()) {
int Use = q.front().first.first;
int cnt = q.front().first.second;
int x = q.front().second.first;
int y = q.front().second.second;
q.pop();
if (x == H - 1 && y == W - 1 && Answer > cnt) Answer=cnt;
/*
* 만약 한번 점프를 쓰고, a,b에 도착을했음. 근데 뒤에서 안쓰고 안쓰고 한번쓰고 a,b에 도착을 하면 굳이 이걸 카운트할 필요가 없잖아
*
*/
//원숭이로 이동
for (int i = 0; i < 4; i++) {
int nx = x + m_dx[i];
int ny = y + m_dy[i];
//Use를 ++ 시키지 않은채로 map이 0이고 범위안벗어나면 넣기
if (nx >= 0 && nx < H && ny >= 0 && ny < W && !visited[nx][ny][Use] && map[nx][ny] == 0) {
visited[nx][ny][Use] = true;
q.push({{ Use,cnt + 1 }, { nx,ny }});
}
}
//말로이동
if (Use < K) {
for (int i = 0; i < 8; i++) {
int nx = x + h_dx[i];
int ny = y + h_dy[i];
if (nx >= 0 && nx < H && ny >= 0 && ny < W && !visited[nx][ny][Use + 1] && map[nx][ny] == 0) {
visited[nx][ny][Use + 1] = true;
q.push({ { Use+1,cnt + 1 }, { nx,ny } });
}
}
}
}
}
int main() {
init();
bfs();
if (Answer == 100000000) { cout << "-1"; }
else {
cout << Answer;
}
return 0;
}