해당 문제는 이 블로그의 글을 보고 풀었습니다.
문제 흐름 도식화 하기
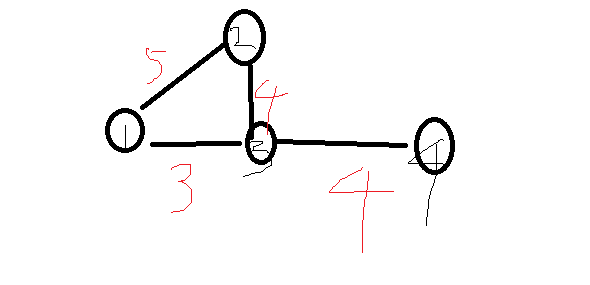
이렇게 그래프가 있다고 치자.
처음에 문제를 읽고, 출발 노드에서 목적 노드까지 도착해야하므로 BFS를 통한 풀이를 생각하였다.
BFS
BFS의 시간복잡도를 살펴보자 BFS의 시간복잡도는 O(N+M) 노드수 + 간선수이다. 왜냐하면, 각 노드를 한번씩 방문하여 visited 체크를 해야하는 N번 그리고 각 노드에서 간선의 수가 M개 있으므로 M을 더하면 시간복잡도 내에 풀이가 가능하다.
그러나 문제는 맨처음 1번노드를 넣고 2번 3번노드를 방문처리를 한뒤에 큐에 넣는다. 문제는 1->2->3->4가 정답인데 이미 앞서서 2번과 3번 노드를 방문 처리하였기 떄문에 2번에서 3번으로 가지 못한다. 고로 1->3->4번의 경우만 탐색이 가능하다.
고로 BFS로는 풀이가 불가능하다.
DFS + 백트래킹
DFS는 어떨까 일반적인 DFS도 방문처리를 하기때문에 풀지 못하지만 백트래킹을 통해 풀면 전체 경우의 수를 파악할 수 있다.
예를들어, 1 2 3 4 경우를 파악한뒤 1 3 4 를 확인할 수 있다. 그러나 이건 시간 초과가 발생한다.
만약 노드가 10000개에서 간선의 갯수가 100,000개 이니까 양방향이므로 200,000개이므로 하나의 노드에서 평균 간선이 20개정도로 예측할 수있다.
그러면 전체 경우의 수는 하나의 노드에서 20개의 간선이 있고, 또 이어진 노드에서 간선이 직전노드를 제외하면 19개 또 다음노드가 18개 이렇게 이어지면 2019...로 무조건 시간초과가 나게 된다.
BFS+이분탐색
위의 그림에서 생각해볼게 있다.
1번노드에서 1을 넣으면 BFS탐색 한번으로 가능한가? 가능하다.
2를 넣어도 가능한가? 가능하다
3도 가능하다
4를 넣으면 1번과 3번의 cost가 3이니까 넣지 않고 2번노드는 5니까 넣을것이다. 그러면 3번노드는 방문처리가 안되어있으므로 2번노드에서 3번노드로 이동이가능하다.
그렇다면 무게 1부터 최고 무게인 1,000,000,000까지 for문을 돌면서 최댓값을 찾으면 된다.
그렇게 되면 O(1,000,000,000 * (N+M))이 된다. 당연히 시간초과가 된다.
이럴떄는 1,000,000,000를 이분탐색으로 가능한 무게를 찾아주면 된다.
그렇게 되면 이분탐색에서 log 1,000,000,000이 10정도니까 풀 수 있다.
//이분탐색코드
int start = 1;
int end = 1000000000;
while (start <= end) {
int mid = (start + end) / 2;
fill(visited, visited + N + 1, false);
if (bfs(mid)) {
start = mid + 1;
if (mid > Answer) Answer = mid;
}
else {
end = mid - 1;
}
}//bfs코드
bool bfs(int weight) {
queue<int>q;
q.push(departure);
visited[departure] = true;
while (!q.empty()) {
int n = q.front();
q.pop();
for (int i = 0; i < map[n].size(); i++) {
int next = map[n][i].first;
int cost = map[n][i].second;
if (!visited[next] && weight <= cost) {
q.push(next);
if (next == arrival) return true;
}
}
}
return false;
}전체코드
int N, M;
vector<vector<pair<int,int>>> graph;
bool visited[10001];
int departure, arrival;
int Answer = 0;
void init() {
cin >> N >> M;
graph.assign(N+1, {});
for (int i = 0; i < M; i++) {
int d, a, cost;
cin >> d >> a >> cost;
graph[d].push_back({a, cost});
graph[a].push_back({d, cost});
}
cin >> departure >> arrival;
}
bool bfs(int weight) {
queue<int> q;
q.push(departure);
visited[departure] = true;
while (!q.empty()) {
int n = q.front();
q.pop();
for (auto &edge : graph[n]) {
int next = edge.first;
int cost = edge.second;
if (!visited[next] && cost >= weight) {
if (next == arrival) return true;
visited[next] = true;
q.push(next);
}
}
}
return false;
}
void solve() {
int start = 1, end = 1000000000;
while (start <= end) {
int mid = (start + end) / 2;
fill(visited, visited + N + 1, false);
if (bfs(mid)) {
Answer = mid;
start = mid + 1;
} else {
end = mid - 1;
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
init();
solve();
cout << Answer;
}중요!!!!!!!
처음에는 vector<pair<int,int>>map[100001]로 썻는데
이것보다
vector<vector<pair<int,int>>>map;하고 N으로 resize를 하는게 좋다.
map.assign(100001,{});
그리고 사용은 동일하게 배열처럼 쓰면된다.