진짜 어려웠던 문제...
Back Tracking에 사고가 매몰되니까 도저히 어떻게 풀이를 해야할지 감이 안잡혀
이틀정도 고민하다.
결국, 답안을 보고 문제를 풀었다.
이 문제의 핵심은 한가지다.
모든 노드를 끝까지 탐색할 필요가 없다는것이다.
문제 예시 2번을 보자.
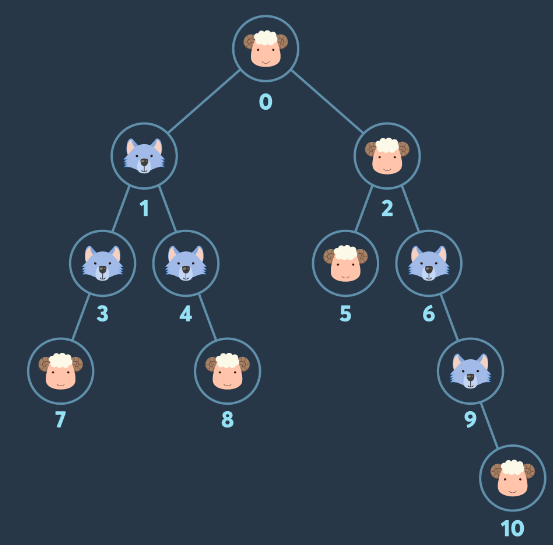
이 문제의 해답은 0-2-5-1-3-7-4-8 순서로 노드를 방문하는것이다.
여기서 볼드처리해놓은 1-3-7-4-8이 중요한데,
DFS 혹은 BackTraking으로 문제를 구현 하는경우,
일단 노드의 끝까지 가야한다는것이다.
만약 DFS나 BT로 구현을 했다면, 일단 5번들리고 6 9 10 을 방문하려는 시도를 해야한다는것이다.
내가 처음에 왜 BackTracking으로 풀어야겠다 라고 생각을 했냐면,
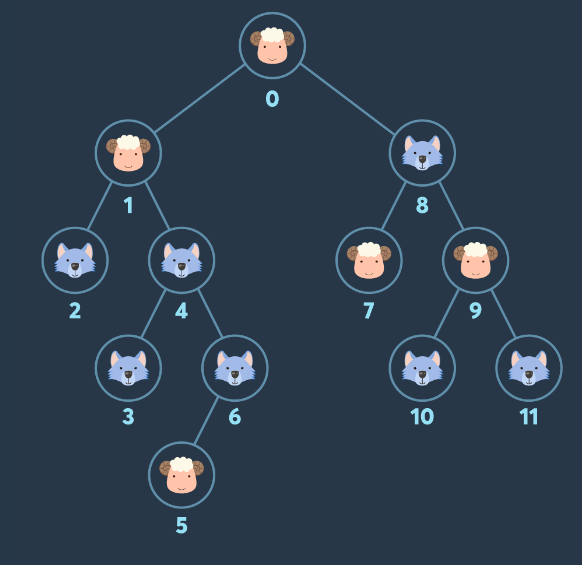
예시 1번을 보면->방문은 노드가 작은 순서대로하고, 노드 방문 가능 여부를 판단하지 않고 일단 우연치않게 1번 노드에 양이 있다고 가정
해보면,
Back Tracking으로 구현시
| sheep | wolf | Node 순서 | 양 Max |
|---|---|---|---|
| 1 | 0 | 0 | 1 |
| 2 | 0 | 0->1 | 2 |
| 2 | 1 | 0->1->2 | 2 |
| 2 | 2 | 0->1->2->4 | 0 |
| 1 | 0 | 0->1->2->4->8 | 0 |
그뒤로는 탐색 불가능
이런식으로, 한번 일단 DFS나 BackTracking으로 구현을 해버리면,
왼쪽이던 오른쪽이던 출발을 해버리면,
왼쪽 트리를 전부 검사하기 전까지는 오른쪽 트리로 이동을 못한다는 말이다.
더 쉽게 풀어서 설명하자면,
일단 0번 노드에서 1번노드로 출발을 해버리면 1번 트리(왼쪽)을 전부 다 검사하기 전까지는 도중에, 8번 노드로 올 수 가 없다는 말이다.
그런데 문제의 핵심이라고 말했던것 처럼 이러한 경우에는 0->1->8번으로 이동이 가능하게 해야한다.
그래서 나는 도대체 DFS,BT가 아니면 어떤형태로 풀어야할지 감이 도저히 잡히지 않았다.
그래서 처음에 시도를 한게 BackTracking을 하기는 하되,
어차피 양의 최대값만 난 알면되는것이니까
방문할때마다, 양과 늑대의 갯수를 저장하면서 가는 방식을 선택하려했다.
그러니까 DFS,BT의 파라미터에 queue를 하나 넣고 여기에 방문했을때의 양과 늑대의 정보를 넣어두는것이다.
예를들면,
0번 노드->{1,0}
1번 노드->{1,0} {2,0}
왜? 여기서 {1,0}을 안지우냐면 1번 왼쪽 트리 전부 검사후 8번 오른쪽 트리 검사할때 이 {1,0}없이 그냥 {2,0}으로만 확인하면, 0번노드->8번노드로 가는 경우 검사가 불가능 하기 때문이다.
고로, 방문 노드마다 생기는 경우를 전부 queue에 넣고 마치려고했다.
그런데 이렇게 해도 문제인게 결국 0번노드에서 1번노드로 가고 왼쪽트리 검사 다 한후에 8번노드로 가서 오른쪽 트리를 검사한다고 쳐도,
0->8->7->9->1 이 경우를 확인을 못한다 왜? 1번 노드는 이미 확인을 했으니까.
진짜 돌아버리는줄 알았다. 도대체 이 문제는 어떻게 풀어야하는건지 감조차 잡히지 않았다.
결국 답안을 확인했고, 어떤 블로그의 코드를 참고해서 문제를 풀었다.
결국 이 문제는 BackTraking이긴한데,
핵심은 간단하게 이거다 =>
1번노드를 통해서 내가 이미 2번노드를 방문을 했어.
근데 이미 방문한 2번노드를 8번 노드를 갔다가 다시 2번노드를 어떻게 방문하지?(왜냐하면 8번노드로 갔다는 말은 이미 왼쪽트리인 1번 노드 트리를 전부 방문을 이미 했으니까) 이게 핵심인 문제였다.
당연히 한글로 보면 이해가 안가니 예시를 들어보자
자 queue가 있다.
그리고 일단 작은것부터 방문한다고 가정을하고
0번 노드부터 시작하니까 일단 0을 넣자
q: 0
q에있는 0번노드를 pop하고
0번노드에서 for문을 돌리면
q: 1,8일것이다.
그러면 이제 1번노드로 가는것이다.
q에있는 1번 노드를 pop하고
1번노드에서 for문을 돌리면
q: 8,2,4 일것이다.
그다음에 8번노드로 가서
q: 2,4,7,9로 q에 넣으면
어? 이러면 안되는거 아닌가? 싶어야한다.
왜냐하면 1번노드는 이미 방문을 해서 q에서 빼줬고 여기서 8번노드를 방문해서 빼주면
아까 위에서 말했던것처럼
0->1->8 경우의 수는 판단이 가능해도
0->8->1의 경우의수는 죽었다 깨어나도 확인이 안된다.
그래서, 이 코드 한줄을 추가해 줘야한다.
이 코드 짜신분.. 천재인거같다...
DFS CODE
void DFS(int currentNode, int sheep, int wolf , queue<int> q, vector<int> &info){
if (info[currentNode] == 0) {
sheep++;
} else {
wolf++;
}
if(wolf>=sheep) return;
if(answer < sheep) answer = sheep;
//예제 1번->0번노드에서 1번,8번 노드 추가
for(int i=0;i<graph[currentNode].size();i++){
q.push(graph[currentNode][i]);
}
//만약 늑대가 sheep의 갯수보다 이상이면 그 뒤에 노드 탐색 필요 x
if(wolf>=sheep){
return ;
}
for(int i=0;i<q.size();i++){
int next = q.front();
q.pop();
DFS(next,sheep,wolf,q,info);
******q.push(next);
}
}DFS로 끝난다음에 BackTracking처럼 이미 방문한 노드를 다시 넣어줘야한다.
이게 왜 그렇지?
다시한번 돌아가보자
양과 늑대의 갯수는 알아서 세라
0번노드: 1,8 <=큐에있는 노드
1번노드: 8,2,4
8번노드: 2,4,7,9 q.front()로 앞에꺼 부터 확인하니까
2번노드: 더이상 자식이 없다. 그러면 DFS재귀 호출 나와서
q.push(2);를 한다.
이러면 q가 4,7,9,2가 된다.
왜 2를 넣는지 이해하기 힘들겟지만 조금만 넘어가보자.
4번노드: 7,9,2,4 (3,6번 노드는 늑대가 더많아서 push안댐)
7번노드: 여기서 확인할 수 있는게
지금 우리가 노드를 방문한 순서를 봐보자.
0->1->8->2->4->7 순서이다.
만약에 q에다가 이미 방문한 2,4번을 넣어주지 않았다면
0->1->8->7->2->4 이 경우로 2번과 4번노드를 다시 방문하지 못할 것이다.
7번노드가 지나면 9,2,4이다. 일단 생략하기 위해서 9번노드의 트리가 없다고 가정해보자 그러면 2,4 아닌가?
지금 현재 0,1,7번노드로부터 양 세마리 8번노드에서 늑대한마리를 가지고 있고
그 다음 q.front인 2번을 방문할 수 있게 된다.
이러면 0->1->8->7->2->4 경우도 확인이 가능하게 된다.
고로 BackTracking을 기존의 비슷한 BackTracking 유형처럼 마치,
0->1->2->1로 다시 돌아오기 위해서 BackTracking을 사용하는것이 아닌,
0->1로 설령 시작을 하여 2번노드를 이미 방문했더라도, 2번 노드를 q뒷편에 넣어서
0->1->8->7->2로 2번을 다시 확인 할 수 있게 만드는것이 핵심인 문제였다.
정답 CODE
#include <string>
#include <vector>
#include <algorithm>
#include <queue>
using namespace std;
vector<int> graph[17];
int answer = 0;
void DFS(int currentNode, int sheep, int wolf , queue<int> q, vector<int> &info){
if (info[currentNode] == 0) {
sheep++;
} else {
wolf++;
}
if(wolf>=sheep) return;
if(answer < sheep) answer = sheep;
//예제 1번->0번노드에서 1번,8번 노드 추가
for(int i=0;i<graph[currentNode].size();i++){
q.push(graph[currentNode][i]);
}
//만약 늑대가 sheep의 갯수보다 이상이면 그 뒤에 노드 탐색 필요 x
if(wolf>=sheep){
return ;
}
for(int i=0;i<q.size();i++){
int next = q.front();
q.pop();
DFS(next,sheep,wolf,q,info);
q.push(next);
}
}
int solution(vector<int> info, vector<vector<int>> edges) {
//graph만들기
for(int i=0;i<edges.size();i++){
int parent = edges[i][0];
int child = edges[i][1];
graph[parent].push_back(child);
}
queue<int> q;
DFS(0,0,0,q,info);
return answer;
}코드의 양을 보면 알 수 있듯이,
와 진짜 어려워서 못풀겠다. 라기 보다는
이게 결국, BackTracking이긴한데 이미 1번노드를 통해서 방문한 2번 노드를 8번 노드를 갔다가 다시 2번노드를 어떻게 방문하지? 이게 핵심인 문제였다.
