이번문제는, 다익스트라를 활용하는 문제이다.
다익스트라로 문제를 풀 생각을 못했던게,
다익스트라는 하나의 노드에서 모든 노드로 가는 최솟값을 구하는 방식이다.
고로, 노드 1번에서 산봉우리 3을 거쳐서 산봉우리5를 가는게 최단거리이면 해당 최단거리가 답이 되는게 다익스트라이다.
고로, 산봉우리를 두번 거쳐서 가는 방법이 존재할 수 있기에 못푼다고 생각했지만.
해당조건을 다익스트라에서 해결해야한다.
사고과정
- 출발점 -> 모든 노드로 가는 과정을 구한다고 치자.
만약 모든출발점으로 for문을 구성한다면 노드의 갯수 50000 * O(200,000log50,000)이므로 시간복잡도가 너무 크다는 점이다.
우리는 어디에서 출발하던 관계없이 하나의 최솟값만 구하면 되므로, 모든 시작지점을 한번에 우선순위 큐에 넣고 시작해야한다.
-
사고과정 변화
출발 점에서 모든 노드로 갈때, 출발 -> 산봉우리 -> 다른 노드 -> 산봉우리 -> ... 이런식으로 갈수도 있다.
고로, 산봉우리를 한번 만나면 산봉우리를 다시 queue에 넣는게 아니라. 거기서 멈춰야한다. -
왕복 편도
출발 -> 산 -> 출발 로 돌아오는게 사실 산에서 출발로 내려올때의 최솟값은 동일하다. 고로 굳이 이것을 왕복으로 구하는게아닌, 편도로 구한다.
코드 설명
const int MAX = 50001;
vector<pii> graph[MAX];
// 출입구에서 다른 지점까지 갈 때 가능한 최소 intensity
int intensities[MAX];
bool isSummit[MAX];
vector<int> answer(2, -1);
intiensities[1]=4이면, 출발지점에서 1번노드까지 최소 거리가 4라는 뜻입니다.
vector<int> solution(int n, vector<vector<int>> paths, vector<int> gates, vector<int> summits) {
fill(intensities, intensities + MAX, 999999999);
for(auto num: summits){
isSummit[num] = true;
}
for(auto path: paths){
int start = path[0];
int end = path[1];
int cost = path[2];
// 양방향 연결
graph[start].push_back({end, cost});
graph[end].push_back({start, cost});
}
dijkstra(gates);
우리는 최솟값을 알아야하니까 intensities를 최대값으로 모두 채워줍니다.
isSummit에 해당 산봉우리를 true로 설정합니다.
paths에 따라 양방향 그래프를 만듭니다.
그리고 다익스트라 인자에 gates벡터를 넣어줍니다.
void dijkstra(vector<int> gates){
// 최소 힙 (intensity가 작은 걸 먼저 꺼내도록)
priority_queue<pair<int,int>> pq;
// 모든 출입구를 출발 노드로 설정한다.
for(auto num: gates){
pq.push({0, num}); // (intensity, 노드 번호)
intensities[num] = 0;
}
...최소힙을 사용합니다. -> 시간복잡도가 줄어듭니다.
원래 다익스트라에는 출발위치를 주어서 해당 출발위치부터 모든 노드까지 최솟값을 구하지만,
우리는 어디에서 출발하던 상관없이 최솟값을 구해야하므로, 큐에 모든 출발 노드를 넣어줍니다. 그리고 intensities는 출발위치니까 0으로 설정합니다.
while(!pq.empty()){
int cost = -pq.top().first;
int now = pq.top().second;
pq.pop();
// 이미 한번 처리된 경우 패스
if(intensities[now] < cost) continue;
cost를 반대로 -로 꺼내줍니다. 왜냐하면 제일 작은거 부터 꺼내야하는데 Priority Queue는 큰값부터 들어가므로 넣을때도 -로 넣어줄겁니다.
if문은 바로 이 뜻입니다.
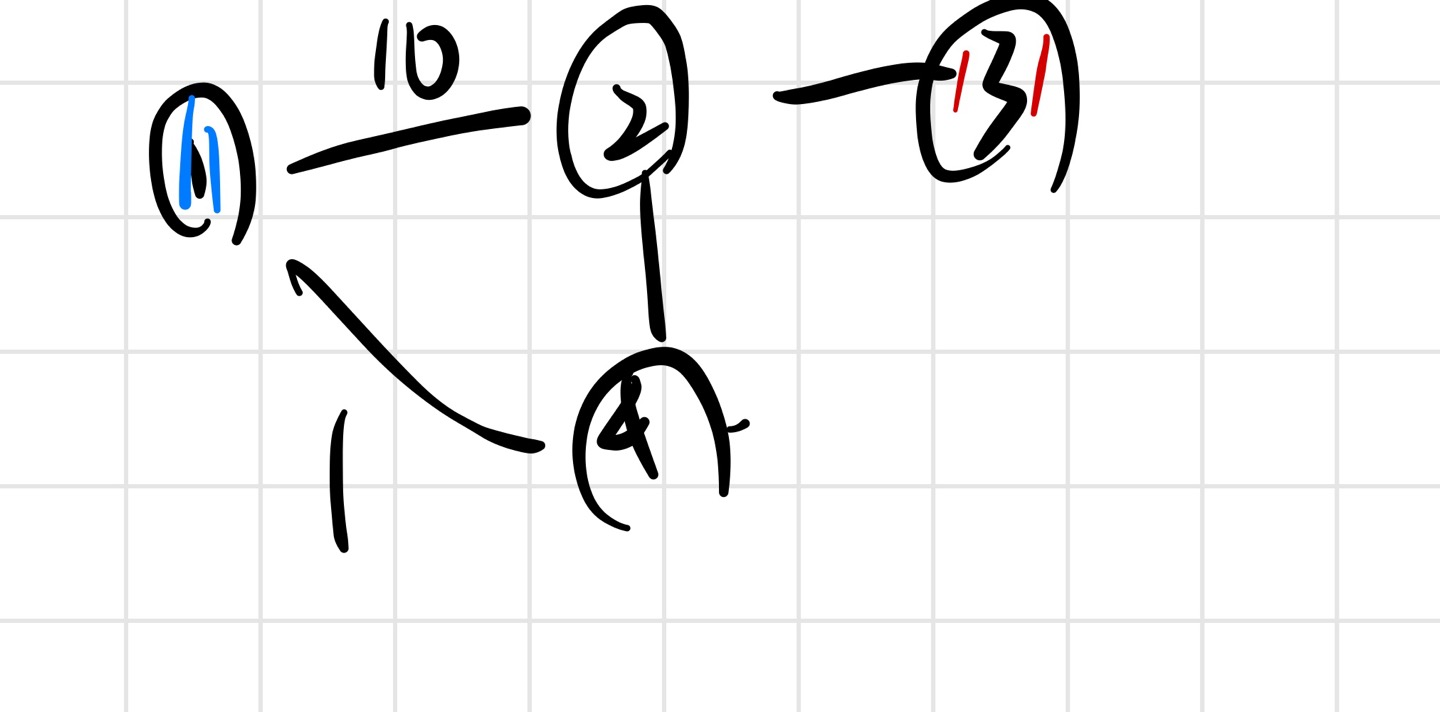
만약 출발점에서 시작하면 intensity[2]=10, intensity[4]=1 그리고 큐에 {10,2},{1,4}가 있을겁니다. 그런데 2번과 4번간선을 1이라 가정하면
intensity[2]=2로 갱신, 그리고 큐에는 {10,2},{4,2}가 존재할겁니다. 이미 2번 노드의 intensity는 2로 갱신이 되었는데 큐에서 10,2를 처리할 이유가 없습니다.
그래서 현재 intensity와 cost값을 비교하여서 cost가 더 큰경우는 고려할 필요가 없으므로 넘깁니다.
// 산봉우리까지 도달한 경우
if(isSummit[now]){
// 산봉우리 번호 & 최소 intensity 갱신
if(answer[0] == -1 || answer[1] > cost){
answer[0] = now;
answer[1] = cost;
}
// 최솟값이 동일한 경우, 산봉우리 번호가 더 낮은 것으로 저장
else if(answer[1] == cost && answer[0] > now)
answer[0] = now;
continue;
}이부분이 출발 -> 산봉우리 -> 노드 -> 산봉우리 경우를 방지하기 위함입니다.
만약에 첫번째 산봉우리에 닿았으면, 정답이거나 최소 intensity를 갱신합니다.
최솟값이 동일하면 산봉우리 번호가 더 낮은 것으로 설정합니다.
그리고 continue로 큐에 넣지 않아 산봉우리에서 다시 시작하는 경우를 없앴습니다.
// 현재 노드와 연결된 모든 노드 탐색
for(auto edge: graph[now]){
int next = edge.first;
int weight = edge.second;
weight = max(weight, cost); // 더 높은 가중치 계산
// 최소 intensity 갱신 (테이블, 우선순위 큐 갱신)
if(
intensities[next] > weight){
intensities[next] = weight;
pq.push({-weight, next});
}
}여기는 원래 다익스트라와 동일합니다. next노드와 다음 노드까지 가는데 cost를 가져와서 만약에 intensity[next]보다 더 작다면 -로 넣어줍니다. 왜냐하면 priority queue는 큰값부터 들어가기 때문에 -로 작게 만들어서 넣어줍니다.
정답코드
#include <string>
#include <vector>
#include <queue>
#include <algorithm>
#include <iostream>
using namespace std;
typedef pair<int, int> pii;
const int MAX = 50001;
vector<pii> graph[MAX];
// 출입구에서 다른 지점까지 갈 때 가능한 최소 intensity
int intensities[MAX];
bool isSummit[MAX];
vector<int> answer(2, -1);
void dijkstra(vector<int> gates){
// 최소 힙 (intensity가 작은 걸 먼저 꺼내도록)
priority_queue<pair<int,int>> pq;
// 모든 출입구를 출발 노드로 설정한다.
for(auto num: gates){
pq.push({0, num}); // (intensity, 노드 번호)
intensities[num] = 0;
}
while(!pq.empty()){
int cost = -pq.top().first;
int now = pq.top().second;
pq.pop();
// 이미 한번 처리된 경우 패스
if(intensities[now] < cost) continue;
// 산봉우리까지 도달한 경우
if(isSummit[now]){
// 산봉우리 번호 & 최소 intensity 갱신
if(answer[0] == -1 || answer[1] > cost){
answer[0] = now;
answer[1] = cost;
}
// 최솟값이 동일한 경우, 산봉우리 번호가 더 낮은 것으로 저장
else if(answer[1] == cost && answer[0] > now)
answer[0] = now;
continue;
}
// 현재 노드와 연결된 모든 노드 탐색
for(auto edge: graph[now]){
int next = edge.first;
int weight = edge.second;
weight = max(weight, cost); // 더 높은 가중치 계산
// 최소 intensity 갱신 (테이블, 우선순위 큐 갱신)
if(
intensities[next] > weight){
intensities[next] = weight;
pq.push({-weight, next});
}
}
}
}
vector<int> solution(int n, vector<vector<int>> paths, vector<int> gates, vector<int> summits) {
fill(intensities, intensities + MAX, 999999999);
for(auto num: summits){
isSummit[num] = true;
}
for(auto path: paths){
int start = path[0];
int end = path[1];
int cost = path[2];
// 양방향 연결
graph[start].push_back({end, cost});
graph[end].push_back({start, cost});
}
dijkstra(gates);
return answer;
}이게 3단계라니 말이 안됩니다. ㅠ
