Lv2라고 하기에는 좀 어려웠던 문제.. 알고나니까 쉬운??
잡설은 그만하고 바로 들어가자
이 문제의 쟁점은 아래와같다.
- 생점을 구해야한다.
- 생점에서 출발하여 생점의 자식노드의 그래프가 막대인지, 도넛인지, 8자인지 알아야한다.
1번부터 해결해보자.
문제에 아래와 같은 조건이 존재한다.
도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프의 수의 합은 2이상입니다.
이말은, 생점은 나가는 자식노드가 최소 2개이상, 생점이니까 들어오는 간선이 0인 노드가 바로 생점이 된다.
//graph를 만들때 그냥 만드는게 아니라, 3,4면 onode는 나가는 노드이므로 onode[3]추가, 들어오는 노드는 inode[4]추가
for (int i = 0; i < edges.size(); i++) {
graph[edges[i][0]].push_back(edges[i][1]);
onode[edges[i][0]]++;
inode[edges[i][1]]++;
}
// 포문을 돌면서 onode[i]가 2 이상이면서 inode가 0인것이 생점이다.
for (int i = 0; i < 1000010; i++) {
if (onode[i] >= 2 && inode[i] == 0) {
answer.push_back(i);
root = i;
}
}그렇다면 질문!
만약, 셍점에서 나가는 그래프의 노드가 2개 이상이라는 조건이 없다면 과연 생점을 찾을 수 있을까?
답은 불가능하다.
왜냐하면, 
빨간색 막대 그래프가 있다고 치고 생점이 파란색이라고 치자, 만약 2개 이상이라는 조건이 없다면, 1번 빨간색 노드가 생점인지 아니면 파란색 노드가 생점인지 알지 못한다.
이제 그래프 모양 갯수를 찾는것을 해보자.
일단 막대 그래프는 더이상 graph에서 탐색할 자식 노드가 없으면, 막대 그래프이다.
8자 그래프는 자식 노드가 2개 이상이면 8자 그래프이다.
도넛그래프가 까다로운데 이것때문에 문제를 풀지 못했다.
처음에는 단순하게 visited[node]해서 방문을 했는데 다시 방문을 했으면 도넛그래프 라고 풀었는데 if문에서 꽤나 애를 먹었다.
코드를 한번 봐보자.
void BFS() {
queue <int> q;
q.push(root);
while (!q.empty()) {
int node = q.front();
q.pop();
visited[node] = true;
if (graph[node].size() >= 2 && node != root) {
eight++;
}
else if (graph[node].size() == 0) {
mak++;
}else if(visited[node]=true){
donut++;
}
else {
for (int i = 0; i < graph[node].size(); i++) {
if(!visited[graph[node][i]]) q.push(graph[node][i]);
}
}
}
}우선 8자 그래프는 root노드가 아니면서(왜냐하면 기본적으로 root 노드는 자식노드가 2개이상), 자식 노드가 2개이상이면 eight을 ++해줬다.
막대 노드는 더이상 탐색할 자식노드가 없으면 ++해줬다.
마지막으로 visited[node] =true를 통해 할라 했는데, 되지 않는다. 그이유가 뭘까?
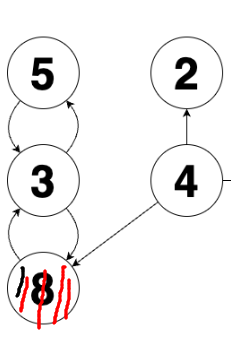
2번 예시에서 queue에서 8번 노드를 꺼내고 visited처리하고, if문 탐색을하면 visited[node]는 아까 위에서 방문처리를 했으므로, 해당 if문에 걸리게 된다.
그게 아니라, 그럼
for (int i = 0; i < graph[node].size(); i++) {
if(!visited[graph[node][i]]) q.push(graph[node][i]);
visited[grap[node][i]]=true;
}여기다가 해줘도, 동일하게 if문에서 걸린다.
그래서 해결한 방법은 그래프의 종류는 오직, 막대, 8자, 도넛 밖에 없으므로, 막대와 8자 그래프를 세고 root노드의 자식노드 개수 에서 막대 8자 그래프의 갯수를 빼주면 자동적으로 도넛노드의 갯수가 된다.
정답 코드
#include <string>
#include <vector>
#include <iostream>
#include <queue>
using namespace std;
int inode[1000010];
int onode[1000010];
vector <int> graph[1000010];
int root = 0;
vector<int> answer;
bool visited[1000010];
int eight = 0;
int mak = 0;
int donut = 0;
void BFS() {
queue <int> q;
q.push(root);
while (!q.empty()) {
int node = q.front();
q.pop();
visited[node] = true;
if (graph[node].size() >= 2 && node != root) {
eight++;
}
else if (graph[node].size() == 0) {
mak++;
}
else {
for (int i = 0; i < graph[node].size(); i++) {
if(!visited[graph[node][i]]) q.push(graph[node][i]);
}
}
}
}
vector<int> solution(vector<vector<int>> edges) {
for (int i = 0; i < edges.size(); i++) {
graph[edges[i][0]].push_back(edges[i][1]);
onode[edges[i][0]]++;
inode[edges[i][1]]++;
}
for (int i = 0; i < 1000010; i++) {
if (onode[i] >= 2 && inode[i] == 0) {
answer.push_back(i);
root = i;
}
}
BFS();
donut = graph[root].size() - mak - eight;
answer.push_back(donut);
answer.push_back(mak);
answer.push_back(eight);
return answer;
}
이 문제는 문제퀄이 ㅎㄷㄷ하다. 굉장히 잘만든 문제같다...
