해당 문제는 위상정렬 + DP 문제입니다.
위상정렬이란?
사이클이 없는 방향 그래프의 모든 노드를 순서대로 나열하는 것을 의미한다.
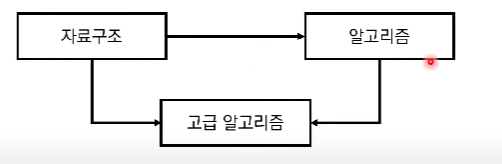
세 과목을 모두 수강하기위한 순서는
자료구조 -> 알고리즘 -> 고급알고리즘 (O)
자료구조 -> 고급 알고리즘 -> 알고리즘 (X)
이를 위해서는 진입차수가 0인 노드들을 확인해야한다.
- 진입차수가 0인 모든 노드를 큐에 넣는다.
- 큐가 빌때까지 다음의 과정을 반복한다.
큐에서 원소를 꺼내 해당 노드에서 나가는 간선을 그래프에서 제거한다.
새롭게 진입차수가 0이된 노드를 큐에 넣는다.
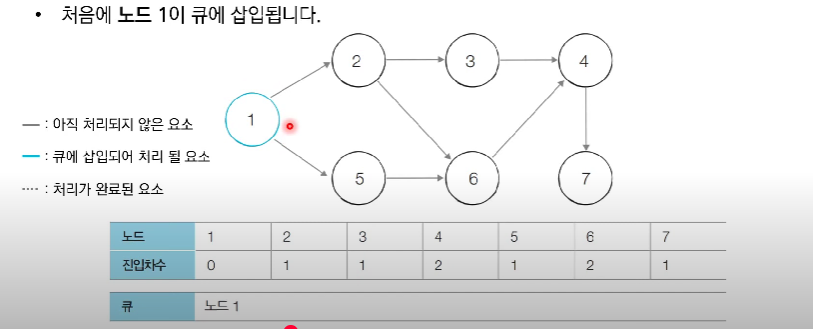
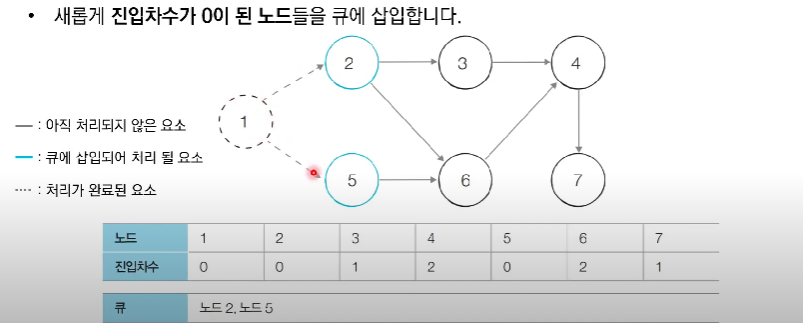
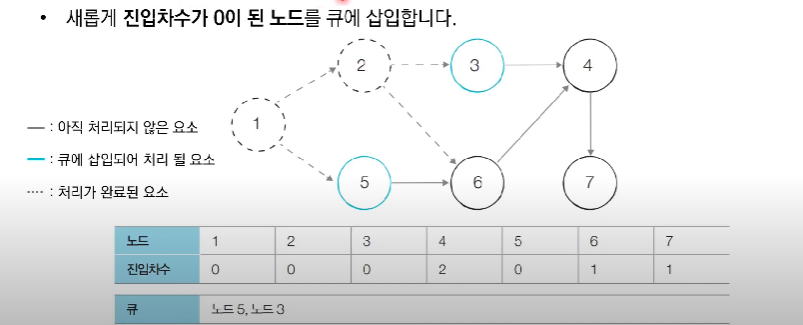
해당 문제를 보면, 위상정렬의 특징을 알 수 있는데, 반드시 직전의 건물들이 모두 지어져야 현재 건물을 지을 수 있다는점에서 확인 할 수 있다.
위상정렬 코드
//노드의 갯수 v, 간선의 갯수 e
int v, e;
//들어오는 차수
int indegree[10001];
vector<int> graph[10001];
//위상정렬함수
void topologySort(){
vector<int> result;
queue<int> q;
for(int i=1;i<=v;i++){
if(indegree[i]==0) q.push(i);
}
while(!q.empty()){
int now = q.front();
q.pop();
result.push_back(now);
for(int i=0;i<graph[now].size();i++){
indegree[graph[[now][i]]]-=1;
if(indegree[graph[now][i]]==0) q.push(graph[now][i]);
}
}
for(int i=0;i<result.size();i++){
cout<< result[i] << ' ';
}
}사이클이 없어야하는 이유가 바로, 사이클이 존재하면 진입차수가 0인 노드가 아에 없기 때문입니다.
틀린코드
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#include <queue>
#include <cstring>
using namespace std;
int N;
int K;
int Time[1001];
vector<int> graph[1001];
int indegree[1001];
int target;
int Max = 0;
void topologysort() {
queue<pair<int, int>>q;
for (int i = 1; i <= N; i++) {
if (indegree[i] == 0) q.push({ i,Time[i] });
}
while (!q.empty()) {
int now = q.front().first;
int cost = q.front().second;
q.pop();
for (int i = 0; i < graph[now].size(); i++) {
if (graph[now][i] == target && Max < Time[graph[now][i]] + cost) Max = Time[graph[now][i]] + cost;
indegree[graph[now][i]] -= 1;
if (indegree[graph[now][i]] == 0) q.push({ graph[now][i], cost + Time[graph[now][i]] });
}
}
}
int main() {
int T = 0;
cin >> T;
for (int i = 0; i < T; i++) {
cin >> N >> K;
for (int j = 1; j <= N; j++) {
cin >> Time[j];
}
for (int j = 0; j < K; j++) {
int a = 0;
int b = 0;
cin >> a >> b;
graph[a].push_back(b);
indegree[b] += 1;
}
cin >> target;
topologysort();
cout << Max << "\n";
//초기화
Max = 0;
memset(Time, 0, sizeof(Time));
memset(indegree, 0, sizeof(indegree));
for (int i = 0; i < 1001; i++) {
graph[i].clear();
}
}
}
해당 코드의 핵심은 queue에 넣을때 지금까지 거쳐온 건물 짓는 시간을 같이 넣는것이다.
첫번째가 노드 숫자고, 두번째가 해당 건물을 지을때 까지 걸린 시간이다.
if (graph[now][i] == target && Max < Time[graph[now][i]] + cost) Max = Time[graph[now][i]] + cost;
이부분에서 어차피 우리는 target의 max값만 알고 싶은거니까,
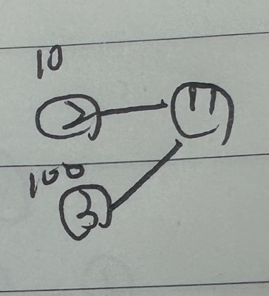
이렇게 7번 노드가 타겟이면, 2번노드에서 Max값과 비교 3번노드에서 Max값과 비교하니까 이렇게만 해도 되는줄 알았다.
그런데 문제가 있다.
2번 노드와 3번노드는 진입노드가 아무것도 없으니까 괜찮은데,
2번노드 뒤에 다른 진입노드들이 있다면 항상 최대 값임을 보장하지 않는다는 것이다.
예를 들어보자,
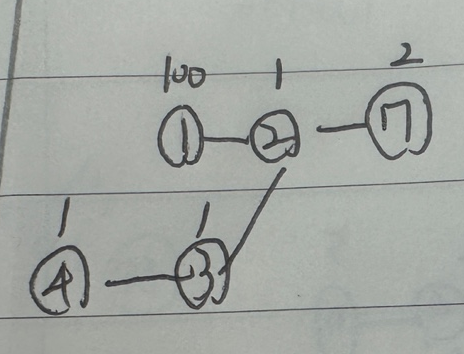
맨처음에 <1,100> <4,1> 이 큐에 들어갈 것이다.
그다음
<1,100>에서는 간선을 --시키고 3번노드와 2번노드가 연결되어있으므로 그냥 넘어간다.
<4,1>에서 <3,2>가되고, <2,3>이 된다 왜냐하면 이미 간선을 줄여놨기 때문이다.
고로, 2번까지의 총 시간이 3이 되는것이다 원래는 101인데 말이다.
고로 DP를 사용하여서 Max값을 갱신해가면서 적어줘야한다.
정답코드
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#include <queue>
#include <cstring>
using namespace std;
int N;
int K;
int Time[1001];
int Dp[1001];
vector<int> graph[1001];
int indegree[1001];
int target;
int Max = 0;
void topologysort() {
queue<int>q;
for (int i = 1; i <= N; i++) {
if (indegree[i] == 0) q.push(i);
Dp[i] = Time[i];
}
while (!q.empty()) {
int now = q.front();
q.pop();
for (int i = 0; i < graph[now].size(); i++) {
int next = graph[now][i];
indegree[next] -= 1;
if (Dp[next] < Time[next] + Dp[now]) Dp[next] = Time[next] + Dp[now];
if (indegree[next] == 0) q.push(next);
}
}
}
int main() {
int T = 0;
cin >> T;
for (int i = 0; i < T; i++) {
cin >> N >> K;
for (int j = 1; j <= N; j++) {
cin >> Time[j];
}
for (int j = 0; j < K; j++) {
int a = 0;
int b = 0;
cin >> a >> b;
graph[a].push_back(b);
indegree[b] += 1;
}
cin >> target;
topologysort();
cout << Dp[target] << "\n";
//초기화
Max = 0;
memset(Time, 0, sizeof(Time));
memset(indegree, 0, sizeof(indegree));
memset(Dp, 0, sizeof(Dp));
for (int i = 0; i < 1001; i++) {
graph[i].clear();
}
}
}
