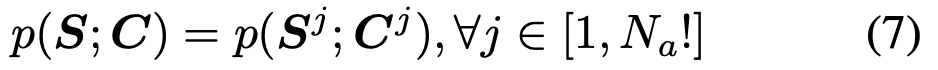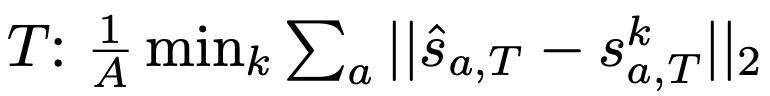[generation][23, 6][86] MotionDiffuser: Controllable Multi-Agent Motion Prediction using Diffusion

ad_official·2024년 12월 31일
0

realistic traffic agent modeling

목록 보기
4/6

-1. 바쁘신 분들을 위한 3줄 요약

  • https://arxiv.org/pdf/2206.00364 기반의 Diffusion model을 multi-agent prediction 연구에 적용 (DDPM/DDIM 계열과 좀 달라 어려웠다.)
  • PCA를 이용해서 diffusion model의 input/output 궤적 차원을 축소 -> 계산량 감소 및 성능 향상
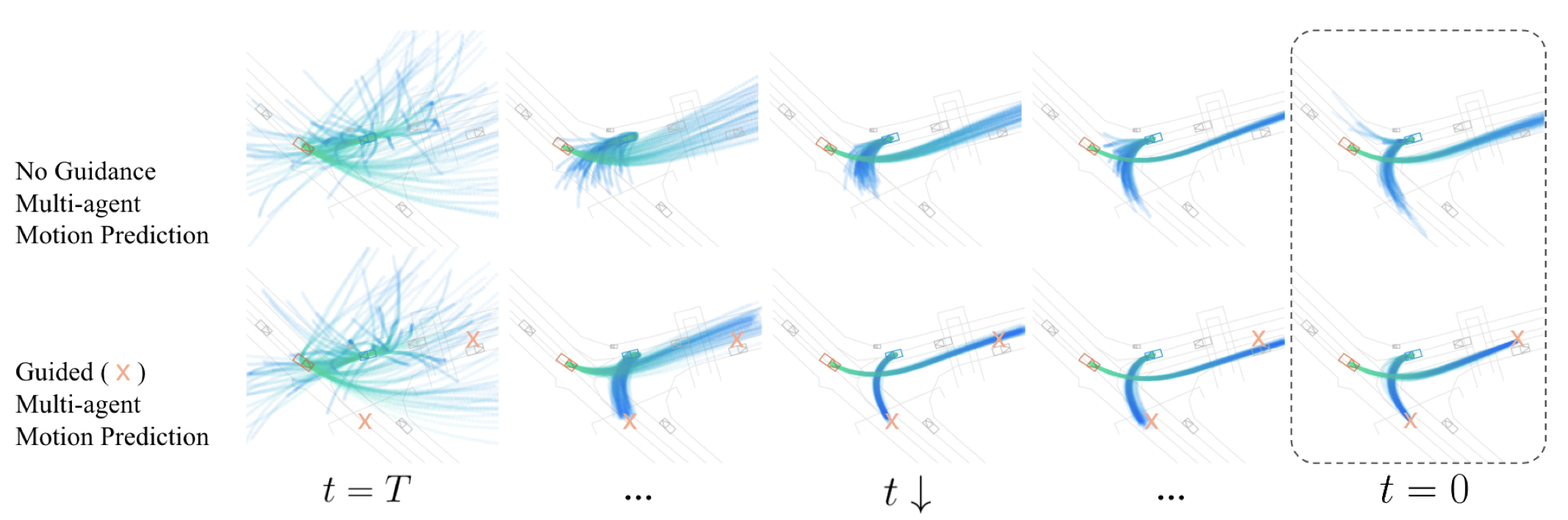
  • 미분가능한 함수로 표현 가능한 어떠한 constraint도 사용할 수 있는, guidance sampling 기법 소개

0. 네트워크 아키텍쳐와 개요

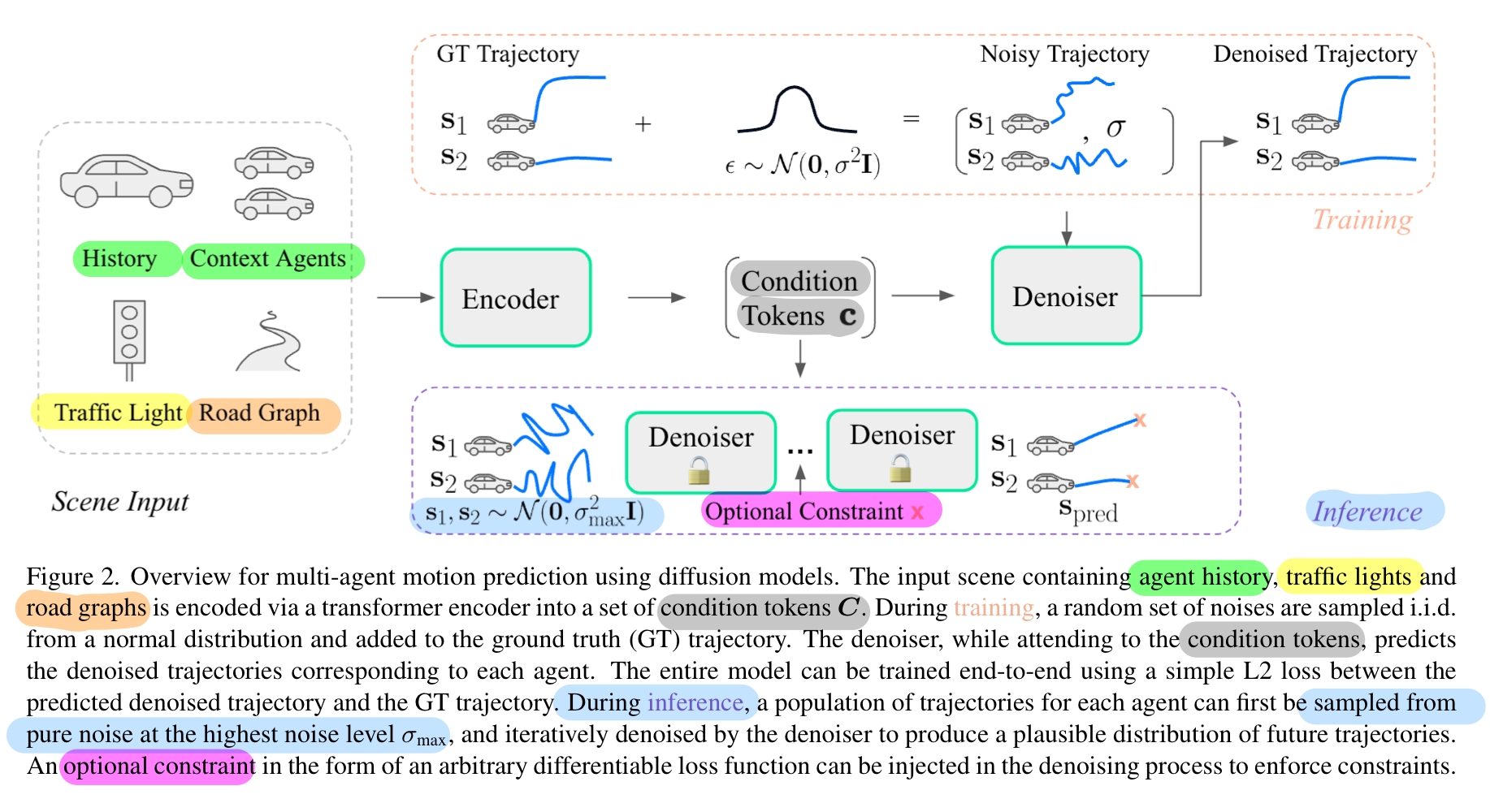
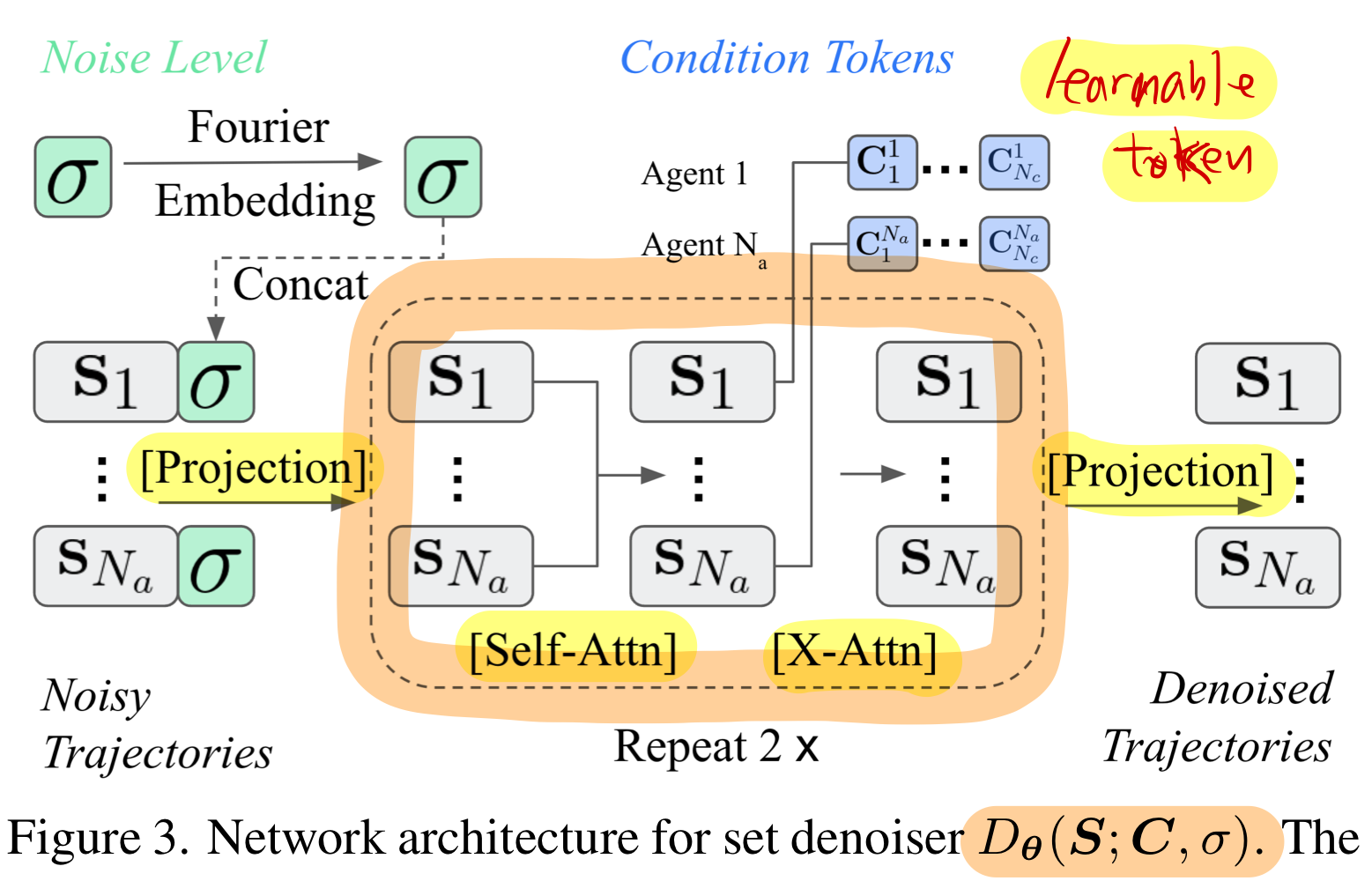
  • Wayformer와 똑같은 backbone을 썼다고 합니다.
  • 학습시 diffusion model의 input
    • multi-agent 궤적 데이터에 노이즈를 주입한 것
  • 학습시 diffusion model의 output
    • 노이즈가 제거된 multi-agent 궤적 데이터
  • inference시 diffusion model의 input
    • unit gaussian에서 random하게 추출한 multi-agent 경로 궤적
  • inference시 diffusion model의 output
    • 생성된 multi-agent 궤적 데이터

0.1. multiple agents의 공동 분포를 ‘순열 불변(permutation-invariant)’ 방식으로 학습 가능

순열 불변(permutation-invariant)이 왜 중요한가?

  • 보통 한 씬(scene) 안에는 여러 에이전트가 존재합니다(예: 차량 10대, 보행자 5명 등).
  • 순열 불변 모델이란, “에이전트 배열 순서를 바꿔 입력해도 결과(에이전트별 예측)는 동일한(순서만 바뀌는) 형태”를 의미합니다. 즉, 어떤 에이전트가 먼저 오든 나중에 오든 모델은 동일한 관계와 분포를 학습합니다.

MotionDiffuser가 이를 어떻게 달성하는가?

  • 순열 불변 디노이저(denoiser) 아키텍처를 제안합니다.
    • 여기서 디노이저(denoiser)는 확산 모델에서 “노이즈가 섞인 상태에서 원본(미래 궤적)을 복원”하는 역할을 합니다.
    • 이 디노이저가 트랜스포머(transformer) 기반으로 만들어지는데,
      • 시간에 대한 positional encoding은 주입하지만,
      • 에이전트 순서에 대한 positional encoding은 주입하지 않습니다.

1. Input/output format: PCA 기반 trajectory representation 압축

  • 한줄요약: 각 궤적( si∈RNt×Nfs_i \in \mathbb{R}^{N_t \times N_f} )을 si∈RNps_i \in \mathbb{R}^{N_p} 로 차원 축소하기
    • N_t: 미래 궤적의 timestep 개수
    • N_f: feature 개수 (x, y, yaw, vx, vy 등)
    • N_p: PCA의 주성분 축
  • PCA는 “데이터를 몇 개의 주요 축(주성분)으로 투영해서, 데이터 분산(=정보)을 최대한 보존하면서 차원을 줄이는 방법”
  • 궤적의 시간적/공간적 구조가 부드러워서 적은 주성분으로도 정보 대부분을 유지 가능
    • 학습데이터를 diffusion network에 입력 전에, 전처리 시 적용
    • 예: 80(N_t)×2(N_f)=160차원을 지닌 궤적이라 해도, 그중 3~10개의 주성분(N_p) 만으로도 데이터의 대부분(99.7%)을 설명할 수 있다고 합니다.

1.1. 왜 궤적을 압축해야 할까?

  • 확산 모델의 샘플링 또는 학습 과정에서, 차원이 너무 커지면 계산량이 폭발하기 쉽습니다.
    • 예: 80개 타임스텝 × 2D 위치만 해도 한 에이전트당 160차원이 되고, 에이전트가 여러 명이면 수백~수천 차원이 됩니다.
  • 또한, 논문에서 제시한 정확한 샘플 로그 확률 계산(Exact log probability inference) ( logp(x(0))log{p(x(0))} ) 을 하려면, 역확산 샘플링 과정에서 매 step 야코비안(Jacobian)의 트레이스(trace)를 계산하는 과정이 필요합니다.
    • 고차원일수록 이 연산이 매우 비싸질 수 있습니다.
    • 야코비안(Jacobian)의 트레이스(trace): 아래에서 자세한 설명 할 것임

1.2. PCA를 적용했을 때의 이점

  1. 모델 성능 개선:
    • 낮은 차원 공간에서 학습하므로 잡음이 줄고 재구성 정확도 가 높아집니다.
  2. 샘플링 및 로그 확률 계산 효율:
    • 차원이 크게 줄어들어 야코비안 계산이나 샘플링 과정이 훨씬 빨라집니다.
  3. 물리적으로도 의미 있는 압축:
    • 궤적 자체가 선형 변환으로 매우 잘 설명될 수 있으므로(“직진 + 가속”처럼 비교적 간단한 모양), PCA가 실제 물리적 해석에도 도움이 됩니다.
  4. 제어된 궤적 생성(Better Success with Controlled Trajectory):
    • 저차원 공간에서는 제어 변수가 적기 때문에 궤적의 제어 및 수정이 더 용이합니다.
    • 이는 제약 조건을 적용할 때 유리합니다.

1.3 PCA를 통한 궤적 데이터 표현 과정

데이터 전처리

  1. 데이터 셋에서, missing data 처리:

    • 실제 환경에서는 노출(occlusion)이나 에이전트가 장면을 떠나는 경우 등으로 인해 궤적 데이터에 결측 시간 단계(missing time steps)가 발생할 수 있습니다.
    • 이를 선형 보간(linear interpolation) 또는 외삽(extrapolation)을 통해 채워 넣습니다.

  2. 샘플링 및 정규화:

    • 궤적 샘플링: ( N_s = 10^5 )개의 에이전트 궤적을 균일하게 샘플링합니다.

      • 기존 데이터 셋에서 NsN_s 개의 데이터 궤적을 활용하겠다는 뜻임

    • 중심화 및 회전:

      • 각 궤적( si∈RNt×Nfs_i \in \mathbb{R}^{N_t \times N_f} ) 를 에이전트의 현재 위치를 중심으로 중심화합니다.
      • 에이전트의 방향(heading)이 +y 방향을 향하도록 회전시킵니다.

    • 평탄화(Flattening):

      • 시간 단계 ( N_t )과 특성 ( N_f )이 있는 궤적 ( si∈RNt×Nfs_i \in \mathbb{R}^{N_t \times N_f} )를 ( si∈RNtNfs_i \in \mathbb{R}^{N_t N_f} )로 변환.

    • 수학적 표기:

      • S′∈RNs×(NtNf)S' \in \mathbb{R}^{N_s \times (N_t N_f)}
      • 여기서 ( S' )는 샘플링된 에이전트 궤적의 집합입니다.

PCA 수행

  1. 주성분 행렬 계산:

    • 평균 궤적 계산:
      sˉ′∈RNtNf\bar{s}' \in \mathbb{R}^{N_t N_f}
      • 모든 샘플 궤적 ( S' )의 평균을 계산하여 평균 벡터를 구합니다.
    • 주성분 행렬 계산:
      Wpca∈RNp×(NtNf)W_{\text{pca}} \in \mathbb{R}^{N_p \times (N_t N_f)}
      • PCA를 통해 주성분 행렬 ( WpcaW_{\text{pca}} )를 계산합니다.
      • 여기서 ( NpN_p )는 사용할 주성분의 수입니다.
      • Whitening: 각 주성분의 분산을 동일하게 조정하여 독립적인 주성분을 만듭니다.

  2. PCA 변환 및 역변환:

    • PCA 변환(주성분 점수 계산):
      s^i=(si−sˉ′)WpcaT\hat{s}_i = (s_i - \bar{s}') W_{\text{pca}}^T
      • 각 궤적 ( s_i )에서 평균 벡터 ( sˉ′\bar{s}' )를 빼고, 주성분 행렬과 내적하여 저차원 표현 ( s^i\hat{s}_i )를 얻습니다.
    • 역변환(원본 궤적 복원):
      si=s^i(WpcaT)−1+sˉ′s_i = \hat{s}_i (W_{\text{pca}}^T)^{-1} + \bar{s}'
      • 저차원 표현 ( s^i\hat{s}_i )에 역변환 행렬을 곱하고, 평균 벡터를 더하여 원본 궤적 ( s_i )를 복원합니다.

  3. PCA 공간에서의 궤적 표현:

    • PCA 변환된 궤적:
      S∈RNa×NpS \in \mathbb{R}^{N_a \times N_p}
      • 여기서 ( N_a )는 모델링 대상 에이전트 수이고, ( N_p )는 사용된 주성분의 수입니다.
      • 이는 고차원 궤적 데이터를 저차원 잠재 공간으로 변환한 표현입니다.
  • 위 S∈RNa×NpS \in \mathbb{R}^{N_a \times N_p} 는 식 (7)에 쓰입니다.

2. 학습 과정?

  • 노이즈 제거 과정을 학습

“아래 논문의 식 (1)~(3)은, ‘데이터 궤적 분포(p(x))를 직접 모델링하기 어려우니, 각 노이즈 레벨에서 데이터 궤적의 점수 함수를 학습해(=디노이저), 큰 노이즈 상태에서 시작해 점차 깨끗한 샘플로 만들어가는 (미분방정식 기반) 방법으로 샘플링을 한다’는 아이디어를 수식으로 표현한 것이다.”

  • 식 (1): 샘플링(깨끗한 데이터 <- 노이즈 ) 과정의 ODE 표현.
    x0=x(T)+∫T0−σ˙(t) σ(t) ∇xlog⁡pθ(x(t);σ(t)) dtx_0 = x(T) + \int_T^0 -\dot{\sigma}(t)\,\sigma(t)\, \nabla_x \log p_{\theta}(x(t); \sigma(t)) \, dt
  • 식 (2): 점수 함수와 디노이저가 어떻게 연결되는지.
    ∇xlog⁡p(x;σ)=(D(x;σ)−x)σ2\nabla_x \log p(x; \sigma) = \frac{(D(x;\sigma) - x)}{\sigma^2})
  • 식 (3): 디노이저를 어떻게 학습하는지(노이즈 제거 L2 손실 최소화).
    arg⁡min⁡θEx∼pχEσ∼q(σ)Eϵ∼N(0,σ2I)∥Dθ(x+ϵ;σ)−x∥22\arg \min_{\theta} \mathbb{E}_{x \sim p_{\chi}} \mathbb{E}_{\sigma \sim q(\sigma)} \mathbb{E}_{\epsilon \sim \mathcal{N}(0, \sigma^2 I)} \| D_{\theta}(x + \epsilon; \sigma) - x \|_2^2

2.1. 두괄식 설명

  1. (x\mathbf{x}): 우리가 생성하려고 하는 데이터(예: 궤적, 이미지 등)의 벡터 표현.
    • σ: 노이즈의 표준편차 또는 노이즈 레벨
    • ϵ: 무작위 노이즈 샘플을 나타내는 벡터입니다. 보통 가우시안 노이즈에서 샘플링
  2. 점수 함수 (∇xlog⁡pθ(x;σ)\nabla_x \log p_\theta(x;\sigma))를 배우는 대신, 이를 디노이저(DθD_\theta) 형태로 학습하여, “노이즈 추가–제거” 과정을 통해 데이터 분포를 이해하게 됩니다.
  3. 샘플링 공정:
    • 큰 노이즈(가우시안)에서 시작 → 점차 (σ\sigma)를 줄여 가며 → 매 단계 “점수 함수(대신 디노이저)”로 방향을 잡고 → 최종 깨끗한 샘플 (x(0))을 얻음.
  4. 훈련 과정 pseudo code:
    • 훈련 샘플 (x∼pχ(x)x \sim p_\chi(x))에서 다양한 (σ\sigma)와 (ϵ\epsilon)을 섞은 “노이즈 (x\mathbf{x})”를 만든 후,
    • (∥Dθ(x+ϵ;σ)−x∥2\|D_\theta(x + \epsilon; \sigma) - x\|^2)를 최소화하도록 (θ\theta)를 최적화.
    • 이렇게 하면, 모델은 “노이즈가 섞인 입력”을 얼마나 잘 “원본”에 가깝게 복원하는지 배우게 되고, 그것이 곧 점수 함수 학습과 동일해집니다.

2.2. 학습과정: 확률 분포와 Score Function

직접 ‘확률 밀도함수’를 배우기 어려운 이유

  • 논문에서는 (pθ(x)p_{\theta}(x))라는 분포 전체(즉, “데이터 (x\mathbf{x})가 어떤 값일 확률”)를 직접 배우기가 어려운(intractable) 상황이라고 합니다.
    • 생성 모델의 세계에서, 분포 전체를 “정규화(normalize)”하기가 매우 까다로운 경우가 많습니다.
    • 즉 분포 전체의 적분 합을 1로 만드는 수식을 적용하기 매우 까다로운 경우가 많습니다.

훈련 데이터 (χ\chi)

  • (χ={x1,x2,…,xNd}\chi = \{x_1, x_2, \dots, x_{N_d}\}): 우리가 가지고 있는 훈련 샘플들의 집합(예: 수십만 장 이미지, 수많은 궤적 등).
  • 이 훈련 집합의 경험적 분포를 (pχ(x)≈1Nd∑δ(x−xi)p_\chi(x) \approx \frac{1}{N_d}\sum \delta(x - x_i))로 표현할 수 있습니다.
    • (δ\delta)는 디락 델타 함수로, “트레이닝 포인트에 질량이 집중된 분포”라는 의미입니다.

대신 ‘점수 함수(Score Function)’를 학습한다

  • 점수 함수 (∇xlog⁡pθ(x)\nabla_x \log p_{\theta}(x))란, “(x\mathbf{x})라는 지점에서 로그 확률의 기울기(gradient)”입니다.
    • 즉, “이 데이터 포인트 (x\mathbf{x}) 주변에서 존재 확률이 어느 방향으로 얼마나 올라가거나 내려가는가”를 나타냅니다.

(σ\sigma)가 조건부로 등장하는 이유

  • 논문에서는 (σ\sigma)라는 노이즈 레벨에서의 분포 ( pθ(x;σ)\ p_\theta(x; \sigma))를 정의
    • 이는 원 데이터 (xx)에 “정도 (σ\sigma)”의 가우시안 노이즈가 섞인 상태를 생각한 것이고,
  • 각 (σ\sigma)별로 “노이즈가 섞인 데이터”의 확률 분포를 배우면, 노이즈를 제거(denoise)하거나 샘플링하는 방법을 익힐 수 있다고 봅니다.
  • 논문에 따르면, (σ(t)=t\sigma(t) = t)라는 선형(Linear) 스케줄을 쓴다고 언급합니다([23] 참고).
  • (t)가 1에서 0으로 가면, (σ\sigma)도 1에서 0으로 선형으로 줄어듭니다.
  • (t=Tt = T)일 때 (σmax\sigma_\text{max}), 즉 가장 큰 노이즈 상태이고, 이걸 점차 줄여가며 깨끗한 샘플로 만들겠다는 뜻입니다.

2.3. 학습과정: Sampling 공식

x0=x(T)+∫T0−σ˙(t) σ(t) ∇xlog⁡pθ(x(t);σ(t)) dtx_0 = x(T) + \int_T^0 -\dot{\sigma}(t)\,\sigma(t)\, \nabla_x \log p_{\theta}(x(t); \sigma(t)) \, dt (1)

구체적으로는 어떤 과정을 거치나?

  • 여기서 (∇xlog⁡pθ\nabla_x \log p_{\theta})가 바로 “점수 함수”로, ‘여기서 확률이 더 높은 쪽으로 샘플을 이동’시키는 역할을 합니다.

2.4. 학습과정 : 데이터 분포 (pχ(x)p_\chi(x))와 Denoiser

  • 디노이저 (D(x;σ)D(x; \sigma))란?

    • 디노이저(Denoiser): “노이즈가 섞인 샘플” (x\mathbf{x})를 입력받아서, “깨끗한(원본) 샘플”을 예측하는 함수.
    • 식 (2)에서 “(∇xlog⁡p(x;σ)=(D(x;σ)−x)σ2\nabla_x \log p(x; \sigma) = \frac{(D(x;\sigma) - x)}{\sigma^2})”라고 했습니다.
      • 이는 “디노이저가 ((D(x;σ)−x)(D(x;\sigma) - x)) 형태로 원본과 노이즈의 차이를 예측”하는데, 이것이 점수 함수와 직접 연결된다는 의미입니다.

  • (3) 디노이저 훈련: 식 (3)
    arg⁡min⁡θEx∼pχEσ∼q(σ)Eϵ∼N(0,σ2I)∥Dθ(x+ϵ;σ)−x∥22\arg \min_{\theta} \mathbb{E}_{x \sim p_{\chi}} \mathbb{E}_{\sigma \sim q(\sigma)} \mathbb{E}_{\epsilon \sim \mathcal{N}(0, \sigma^2 I)} \| D_{\theta}(x + \epsilon; \sigma) - x \|_2^2 (3)

  • 목표: “노이즈가 (ϵ\epsilon)만큼 섞인 (xx)”를 입력받았을 때, 원래 (xx)를 정확히 복원하도록 (∥Dθ(x+ϵ;σ)−x∥22\|D_\theta(x+\epsilon;\sigma) - x\|_2^2)를 최소화하고자 함.

  • 여러 노이즈 레벨((\sigma))에 대해서도 잘 되도록, (σ\sigma)를 (Eσ∼q(σ)\mathbb{E}_{\sigma \sim q(\sigma)}) 식으로 샘플링하며 학습.

  • 즉, 어느 정도의 노이즈가 섞여도 원본 (x)를 잘 추정하는 함수 (DθD_\theta)를 학습하는 것이 확산 모델의 핵심 아이디어 중 하나입니다.

식 (2)와 식 (3)이 어떻게 연결되는가?

점수 함수 vs. 디노이저

  • 식 (2)
    ∇xlog⁡p(x;σ)=(D(x;σ)−x)σ2\nabla_x \log p(x;\sigma) = \frac{(D(x;\sigma) - x)}{\sigma^2}
    라는 건, “노이즈가 (σ\sigma)만큼 섞인 (x\mathbf{x})를 (xclean\mathbf{x}_{\text{clean}}) = D(x;σ)D(x;\sigma)) 로 복원했을 때, 그 복원 정도가 점수 함수와 비례한다”는 말입니다.
  • 우리가 (3)번 식의 L2 에러를 최소화하는 디노이저 (DθD_\theta)를 학습하면,
    • 결과적으로 (∇xlog⁡pθ(x;σ)\nabla_x \log p_\theta(x;\sigma))도 자동으로 학습된다는 뜻입니다.
  • 이는 “확률 분포 자체를 직접 학습하는 대신, 노이즈 제거 과정을 학습”해서 점수 함수를 얻는 방법으로 이해하시면 됩니다.

2.5. 장점: L2 loss만 사용하고, trajectory anchors에 의존하지 않는 단순한 predictor 구조

  • 배경: 왜 과거 연구에서는 ‘trajectory anchors’를 보통 사용하는가?
    • 모션 예측에서 한 에이전트가 움직일 수 있는 경로는 매우 다양합니다(다중모달성).
      • 예를 들어, 자동차가 직진할 수도 있고, 오른쪽으로 돌 수도 있고, 갑자기 속도를 늦출 수도 있는 등 미래의 가능성이 여러 갈래로 나뉩니다.
    • 이를 효과적으로 모델링하기 위해 기존 많은 모델들은 앵커(anchor) 라 불리는 ‘미리 정해둔 후보 궤적’들을 제안해 왔습니다.
      • 다양한 모드(mode)를 대표하는 다수의 궤적을 설정하고, 그중 어느 궤적이 실제로 일어날지 확률적으로 예측
  • 단일 L2 loss만 사용, 미래 궤적 모드(앵커) 사용 안 함
    • MotionDiffuser는 ‘확산 모델’을 이용함으로써 이러한 복잡한 앵커 구조 없이 다양한 미래 궤적 분포를 자연스럽게 학습.
    • 결과적으로 모델 구조가 간단해지고(추가적인 앵커 설정이나 앵커 선택 로직이 필요 없어 효율적), 다중모달성을 잘 표현할 수 있음.

2.6. 학습 세부 사항: Preconditioning and training

  • Conditional diffusion model 파트는 그냥 읽으면 이해되는 내용
  • TODO
    • Preconditioning and training 파트는 느낌만 이해했음
    • 나중에 필요하면 추가 공부 및 정리 필요

2.7. 디노이저 학습하면 -> 궁극적으로 ‘로그 확률’을 구할수 있게 됨

로그 확률 (log(p(x))을 왜 구하면 좋은가?

  • 모델이 생성한 결과가 얼마나 ‘그럴듯한지’ 확인
    • 확산 모델은 미래 궤적(차가 어디로 갈지) 또는 이미지를 만들어내는 모델
    • 만들기만 해서 끝나면, “이게 정말 말이 되는 결과인지” 평가하기가 어렵죠.
    • 그래서 “이 샘플은 모델이 생각하는 확률 분포에서 얼마나 가능성이 높은가?”를 나타내는 로그 확률 logp(x(0))log{p(x(0))}을 계산하는 방법이 있으면 좋아요.
    • 만약 로그 확률이 너무 낮은 샘플이면, “이거는 현실성이 별로 없는 결과네”라고 걸러낼 수 있어요.

Exact log probability inference with Jacobian trace?

핵심 한 줄 요약

  • “확산 모델에서 로그 확률 계산 ( logp(x(0))log{p(x(0))} )을 위해서는, 샘플링 (역확산) 시 매 시간에 따라 야코비안 트레이스를 계속 적분해야 하는데, 이 연산이 고차원일수록 엄청 비싸기 때문에, PCA로 차원을 줄여서 계산을 훨씬 효율적으로 만든다.”

sampling 과정에서 시간이 지남에 따라 p(t) ‘확률’은 어떻게 바뀔까?

‘밀도’가 바뀌는 걸 ‘divergence’ 개념으로 설명
  • 궤적 공간에서 샘플이 이동하면(시간 t에 따라 궤적이 바뀌면), 그 주위의 밀도(분포)도 함께 변합니다.
  • 이 밀도 변화가 “얼마나 공간을 넓히는가(+) 혹은 좁히는가(-)”로 측정되는데, 이 값이 “발산(divergence) = 야코비안 트레이스”입니다.
  • 그래서 exact log probability inference를 하려면, 이 발산(트레이스)을 계속 추적해 적분해 주어야 하는 것이지요.
    • +: 팽창. 그 구역에 있던 샘플들은 서로 더 멀어지니, 밀도(샘플이 모여 있는 정도)는 낮아집니다.
    • -: 수축. 같은 샘플이라도 더 빽빽이 몰려 밀도가 높아지죠.
  • 이 “얼마나 팽창·수축하느냐” -> divergence = 야코비안(Jacobian)의 트레이스(trace)
  • 그래서, 확산 모델에서 x(t)가 움직일 때 logp(x(t))가 어떻게 변하는지 계산하려면,
    • 결국 “공간을 얼마나 ‘펼치거나(+) 오그라뜨게(-)’ 하는가”인 divergence을 추적해야 하고, 그게 곧 야코비안 트레이스를 구하는 이유입니다.

야코비안(Jacobian)과 트레이스(trace)란?

야코비안(Jacobian)
  • 야코비안은 “함수가 입력받은 여러 변수들(예: x, y, z)에 대해 어떻게 출력값이 변하는지”를 편미분으로 전부 모아놓은 행렬입니다.
    • 예: (f(x,y))라는 함수가 있을 때,
      Jf=[∂f1/∂x∂f1/∂y∂f2/∂x∂f2/∂y]J_f = \begin{bmatrix} \partial f_1 / \partial x & \partial f_1 / \partial y \\ \partial f_2 / \partial x & \partial f_2 / \partial y \end{bmatrix}
      같은 식이에요.
트레이스(trace)
  • 정방행렬(가로·세로 크기가 같은 행렬)에서 대각선에 있는 숫자들을 전부 더한 값이에요.
  • 야코비안이 n×nn \times n이라면, 대각선 원소들의 합이 그 행렬의 트레이스입니다.
  • 물리·수학적으로는 이 트레이스가 “공간이 어느 정도로 팽창(+), 수축(-)하느냐”를 의미할 때가 많습니다.
    • 그래서 이를 “발산(divergence)”이라고 부르기도 해요.

왜 고차원에서는 이게 힘든가?

야코비안 행렬이 (n×nn \times n)
  • 만약 궤적 정보가 200차원이라면, 야코비안은 200×200=40,000개 숫자를 갖는 행렬이에요.
  • 이걸 매 시간 스텝마다 계산하고 더하려면 엄청난 연산이 필요해요.
PCA로 차원을 줄이면?
  • PCA는 “데이터가 실제로는 몇 개의 중요한 축(주성분)으로만 잘 설명된다”는 원리를 이용해서, 고차원 데이터를 저차원으로 ‘똑똑하게’ 압축해 줍니다.
  • 예: 200차원을 10차원으로 줄이면, 이제 야코비안은 10×10 = 100개 원소만 계산하면 되죠.
  • 그래서 계산이 훨씬 빨라져요.

3. 학습 후 , inference sampling (w/o guidance)

3.1. Sampling

한 문장 요약

“Eqn. 1(ODE)를 풀어 노이즈 많은 초기 상태 (x(T))에서 깨끗한 샘플 (x(0))에 도달할 때, 2차 정확도의 Huen 방식을 사용해 단계별로 샘플을 업데이트하며, 그 단계를 32번 수행한다”
x0=x(T)+∫T0−σ˙(t) σ(t) ∇xlog⁡pθ(x(t);σ(t)) dtx_0 = x(T) + \int_T^0 -\dot{\sigma}(t)\,\sigma(t)\, \nabla_x \log p_{\theta}(x(t); \sigma(t)) \, dt (1)
는 뜻입니다. 이를 통해 샘플링 정확도와 계산 효율을 균형 있게 맞추려고 하는 것입니다.

왜 ODE를 써야 하는가?

  • 논문에서는 ODE 공식으로 (x(t)x(t))가 변하는 법칙을 명시해 두었습니다.
  • 실제로는 (σ(t)\sigma(t))가 줄어들면서, (∇xlog⁡pθ(x(t);σ(t))\nabla_x \log p_{\theta}(x(t);\sigma(t)))가 샘플 (x(t)\mathbf{x}(t))을 “더 확률이 높은 방향”으로 이동시키는 식입니다.
  • 이를 한 번에 닫힌 형태로 풀기 어렵기에, 수치 해석 기법(ODE solver)으로 시간이 (T)에서 0으로 흐를 때 (x(t)\mathbf{x}(t))가 어떻게 바뀌는지 단계별로 추적합니다.

Huen’s 2nd order method란?

개념

  • Huen’s method(혹은 Heun’s method)는 2차 정확도(2nd order)를 가지는 Runge-Kutta 계열의 ODE 해법 중 하나입니다.
  • 간단히 말해, 1차(Forward Euler)보다 오차가 훨씬 적고, 완전 4차(고전적 Runge-Kutta)보다는 계산비용이 낮은 중간 수준의 방법입니다.

Huen’s method 동작 원리 (간단 요약)

  1. Predictor(예측 단계):

    • ( xn+1pred=xn+f(tn,xn) Δt\mathbf{x}_{n+1}^{\text{pred}} = \mathbf{x}_n + f\bigl(t_n,\mathbf{x}_n\bigr)\,\Delta t)
    • 여기서 (f)는 ODE의 우변, 즉 (dxdt\frac{dx}{dt})를 의미합니다.

  2. Corrector(보정 단계):

    • ( xn+1=xn+Δt2(f(tn,xn)+f(tn+1,xn+1pred))\mathbf{x}_{n+1} = \mathbf{x}_n + \frac{\Delta t}{2} \Bigl( f\bigl(t_n,\mathbf{x}_n\bigr) + f\bigl(t_{n+1}, \mathbf{x}_{n+1}^{\text{pred}}\bigr) \Bigr) )
  • 이렇게 Predictor–Corrector 두 단계를 거쳐, 한 스텝에서의 오차를 1차보다 효과적으로 줄입니다.

3.2. improved trajectory sample clustering algorithm

  • 이 알고리즘은 모션 예측 모델이 생성한 다수의 샘플(궤적들) 중에서 대표성(representative)을 갖춘 소수의 궤적 집합을 추출하기 위해 사용됩니다.
  • 의문점
    • 애초에 inference 시 sampling 속도가 느리니까, sampling을 많이 못할 것 같은데?
    • 논문에서는 sampling을 한 1000번 하고, 그 중에서 6개 골라내는 식으로 설명하고 있네? 1000개를 언제 다 뽑고 있지?

문제 배경: “왜 샘플 클러스터링이 필요한가?”

모델이 만들어내는 ‘다양한 미래 궤적’

  • 확산 모델(예: MotionDiffuser)은 단일 에이전트 또는 다중 에이전트의 미래 궤적을 다양한 형태로 생성할 수 있습니다.
  • 이처럼 다중모달(multi-modal) 분포로부터 임의 개수의 샘플을 추출할 수 있으니, 이론적으로는 수백~수천 개의 궤적이 생성될 수 있습니다.

최종 제출(또는 활용) 시 제한된 샘플 수

  • 실제 평가나 산업 현장에서는, 너무 많은 궤적을 전부 사용하기 어렵거나, 특정 개수(예: 6개)로 요약이 필요합니다.
    • 예: Waymo Open Motion Dataset의 Interaction Prediction 챌린지에서 6개 예측 궤적만 제출하라는 요구사항이 있을 수 있음.
  • 따라서, 모델이 뽑은 다수의 샘플 중에서 대표성을 갖춘 소수(예: 6개) 궤적을 선택하는 “샘플 클러스터링” 기법이 필요하게 됩니다.

샘플 클러스터링의 기본 아이디어

“대표 모드(Mode)” 추출

  • 여러 개의 미래 궤적 샘플이 있을 때, 서로 형태가 유사한 궤적들끼리 한 군집(cluster)을 이룹니다.
    • 예: “직진 궤적” 군집, “큰 회전 궤적” 군집, “작은 회전 + 감속 궤적” 군집 등.
  • 클러스터링을 통해, 각각의 군집 대표(center)를 골라내면, 이 대표가 해당 군집의 특징(미래 경로 패턴)을 대변합니다.

거리(metric)를 활용한 군집화

  • 논문에서는 특정 고정 거리 임곗값(threshold) 내에 들어오는 샘플들을 하나의 군집으로 묶는 탐욕적(greedy) 알고리즘 접근을 채택합니다([48] 참고).

MotionDiffuser에서의 “개선된(Improved) 샘플 클러스터링” 핵심 포인트

  • MotionDiffuser가 사용하는 클러스터링 기법은 [48]의 “Trajectory Aggregation Method”를 기반으로 몇 가지 개선을 더했다고 언급됩니다. 주요 포인트는 다음과 같습니다.

Iterative Greedy Clustering (반복적 탐욕 군집화)

  1. 샘플 추출: 확산 모델(MotionDiffuser)에서 예를 들어 1,000개의 미래 궤적 샘플을 생성. (다중 에이전트라면, 샘플 하나에 여러 에이전트 궤적 포함)
  • PCA 변환: 각 샘플을 PCA 공간으로 투영하여 차원을 줄인 상태로 diffusion model을 처리했음(거리 계산 효율↑).
  1. Initialize: 클러스터 목록(cluster list)을 비운 상태에서 시작.
  2. While (아직 샘플이 남아 있고, 원하는 클러스터 수 미만이라면):
    1. 모든 남은 샘플 중, “이 샘플을 center로 삼았을 때 몇 개를 커버할 수 있는지” 계산.
    2. 그 중 “가장 많은 샘플”을 커버하는 center(대표)를 찾음.
    3. 그 center에서 임곗값((ϵ\epsilon)) 이하로 떨어져 있는 샘플들을 하나의 군집으로 묶음.
    4. 묶인 샘플들은 후보에서 제거하고, 군집 목록에 등록.
  3. 출력: 최종 군집들의 대표 궤적(또는 군집 평균)을 대표 예측으로 사용.

이렇게 하면, 제한된 개수의 대표 궤적만 뽑아도 분포의 주요 모드들을 잘 반영할 수 있습니다.

‘Joint Prediction’ 셋업에서의 특별 처리

  • 다중 에이전트 공동 예측(Joint Prediction)에서는, “하나의 샘플”이 곧 “모든 에이전트의 궤적 묶음( joint trajectory )”을 의미합니다.
  • 따라서, “샘플 간의 거리”를 계산할 때는 모든 에이전트의 궤적을 동시에 고려해야 합니다.
    • 예: 에이전트 A, B, C가 각각 (x,y) 변화를 80 스텝 간 가지면, 이를 모두 포함해 집합 전체 거리를 계산해야 합니다.
  • MotionDiffuser는 이 부분을 “각 에이전트별로 임곗값 이내에 들어오는지”를 종합적으로 확인하도록 변경(수정)했다고 언급합니다.
    • 즉, A~C 모든 에이전트가 유사하다면 같은 군집으로 묶이도록, 거리 계산을 확장한 것입니다.

고차원 궤적의 효율적 클러스터링

  • 이 과정에서 PCA 기반으로 사전에 궤적 차원을 줄였다면, 거리 계산이나 탐욕적 선택도 훨씬 빨라집니다.
  • 논문에서는, PCA로 궤적 차원을 획기적으로 낮추면(예: 160 → 10 차원), 군집화 연산 역시 비용이 줄어 실시간에 가깝게 혹은 대규모 데이터셋에 대해서 수행 가능해진다고 설명합니다.

왜 “개선된(Improved)”인가?

  • 논문에서 “improved trajectory sample clustering algorithm”이라 표현한 이유는,

    1. 기존 알고리즘([48] 참조)보다 다중 에이전트 공동 예측 상황에 맞게 조정(modification) 했다는 점,
    2. PCA 공간에서 효율적으로 군집화함으로써 성능(정확도 & 속도)을 높였다는 점,
    3. 임곗값 기반 탐욕적 군집을 통해 여러 모드를 효과적으로 커버하면서도 간단한 알고리즘을 유지했다는 점이 결합된 결과로 보입니다.

  • 실제로, Waymo Open Motion Dataset의 Interaction Prediction 과제처럼, ‘6개’ 대표 궤적을 요구하는 경우에 이 기법을 적용하면, 천 개 이상의 샘플을 생성한 뒤, 가장 6개의 대표 모드를 골라낼 수 있습니다. 이로써 충분한 다양성과 적절한 대표성을 확보합니다.

4. 학습 후 , inference sampling (with guidance)

4.1. 결론: 제약 걸린 확산 샘플링의 과정

  1. 결합:

    • 최종적으로 샘플링 시,(p(S;C)⏟원래 궤적 분포×q(S;C)⏟제약 분포\underbrace{p(S;C)}_{\text{원래 궤적 분포}} \times \underbrace{q(S;C)}_{\text{제약 분포}}) 두 항을 합쳐, 각 스텝에서 노이즈를 제거해 나감.
    • 즉, “모델이 학습한 자연스러운 궤적”과 “추가적인 제약”을 모두 반영한 궤적을 생성.

  2. 기존 점수 함수: (∇xlog⁡p(x;σ)=(D(x;σ)−x)σ2\nabla_x \log p(x; \sigma) = \frac{(D(x;\sigma) - x)}{\sigma^2}))

    • 확산 모델이 학습한 “미래 궤적 분포”를 따르는 방향.

  3. 제약 점수 함수: (∇Slog⁡q(S;C,σ)≈λ∂∂SL(D(S;C,σ))\nabla_S \log q(S; C, \sigma)\approx \lambda \frac{\partial}{\partial S} \mathcal{L}(D(S;C,\sigma)))

    • “원하는 물리적·커스텀 조건”을 만족하도록 만드는 방향.

4.2. 결합 분포 샘플링과 ‘점수 함수(Score Function)’

점수 함수(Score) 개념

  • 확산 모델에서, 분포 ( p(S; C) )를 직접 다루기보다는, “로그 확률의 기울기”인 점수 함수 (∇Slog⁡p(S;C)\nabla_S \log p(S;C)\ )를 학습/활용합니다.
  • “결합 분포”의 점수 함수는 다음과 같이 쓸 수 있습니다.
    ∇Slog⁡(p(S;C)⋅q(S;C))=∇Slog⁡p(S;C)+∇Slog⁡q(S;C).\nabla_S \log \bigl(p(S;C) \cdot q(S;C)\bigr) = \nabla_S \log p(S;C) + \nabla_S \log q(S;C).

식 (12)에서 말하는 ‘노이즈 레벨 (σ\sigma)를 고려한 점수’

  • 실제 확산 모델 샘플링 과정에서, “노이즈가 (σ\sigma)만큼 섞인 상태”를 단계별로 디노이징할 때, 모든 단계(노이즈 레벨)에 대한 점수 함수가 필요합니다.
  • 따라서, 식 (12):
    ∇Slog⁡p(S;C,σ)  +  ∇Slog⁡q(S;C,σ)\nabla_S \log p(S;C,\sigma) \;+\; \nabla_S \log q(S;C,\sigma) {12}
  • 참고: (∇xlog⁡p(x;σ)=(D(x;σ)−x)σ2\nabla_x \log p(x; \sigma) = \frac{(D(x;\sigma) - x)}{\sigma^2})

4.4. 제약 그래디언트((∇Slog⁡q(S;C,σ)\nabla_S \log q(S;C,\sigma)))를 어떻게 구하나?

“클래스 분류 기반 가이던스(classifier-based guidance)” 유사

  • 여기서는 “물리 제약”이나 “in-painting 조건” 같은 것을 특정 네트워크가 (∇Slog⁡q(⋅)\nabla_S \log q(\cdot))로 예측할 수도 있고, 혹은 임의의 미분 가능한 비용 함수를 정의해 (추가 학습 네트워크 없이) 그 그래디언트를 이용할 수도 있습니다.

임의의 비용 함수 ( L\mathcal{L} )를 사용하고 싶다

  • 논문에서는 “특수한 네트워크를 훈련하지 않아도, 임의의 미분 가능한(autograd 가능) cost function”을 통해 제약을 표현하겠다고 합니다.
  • 예: (Lcollision(S)\mathcal{L}_{\text{collision}}(S)) = “충돌이 발생하면 큰 값”이 되도록 설계 → 그라디언트를 빼주면 “충돌을 피하는 방향”으로 샘플링.

4.5. 노이즈 상태 (S) vs. 디노이징된 상태 (D(S;C,σ)D(S; C, \sigma))

문제: “노이즈가 섞인 (S)”는 물리적으로 의미가 없을 수 있다.

  • (σ\sigma)가 크면, (S) 자체가 “엉망인 궤적” (데이터 매니폴드 밖)일 수 있음.
  • 그런데 우리가 정의한 물리 제약(충돌 회피 등)은 “물리적으로 그럴듯한 궤적”을 가정해야 적용이 제대로 됩니다.

핵심 아이디어: “(D(S;C,σ)D(S; C, \sigma))”와의 이중성(duality)

  • 논문에 따르면, 디노이저 (D(S;C,σ)D(S; C, \sigma))는 “노이즈가 섞인 (S)”를 입력받아, (상대적으로) “물리적으로 타당한” 궤적을 근사해 줍니다.
    • 아무리 (\sigma)가 커도, 모델은 “학습된 데이터”에 맞추어 되도록 유사한 궤적을 예측하려고 하죠.
  • 그래서, “노이즈가 섞인 (S)”에 제약을 적용하기보다는, 그에 대응되는 “디노이징된 결과 (D(S;C,σS;C,\sigma))”에 대해 비용 함수를 계산하면, 더 현실적인 제약을 반영할 수 있습니다.

4.6. 식 (13): 제약 그래디언트 추정

∇Slog⁡q(S;C,σ)  ≈  λ  ∂∂S  L(D(S;C,σ)).\nabla_S \log q(S;C,\sigma) \;\approx\; \lambda \;\frac{\partial}{\partial S}\; \mathcal{L}\bigl(D(S;C,\sigma)\bigr). (13)

식 (13) 해석

  • ( ∇Slog⁡q(S;C,σ)\nabla_S \log q(S;C,\sigma)): “노이즈 상태 (S)”에서의 제약 분포의 점수(로그 확률 기울기).
  • (L(D(S;C,σ))\mathcal{L}(D(S;C,\sigma))): “디노이저가 복원한 궤적”에 대해 정의된 임의의 비용 함수(예: 충돌 점수, 특정 위치 도달 점수 등).
  • (∂∂S\frac{\partial}{\partial S}): “(S)”(노이즈 상태)에 대한 편미분.
    • 실제 비용은 “(D(S))”에 정의되었지만, 체인 룰(chain rule)에 의해 (∂L/∂S\partial \mathcal{L}/\partial S)로 바꿀 수 있습니다.
  • (λ\lambda):하이퍼파라미터로, “제약의 강도”를 조절합니다.

4.7. 예: Repeller Cost

Repeller Cost의 역할

  • Repeller Cost는 에이전트 간의 거리가 너무 가까워지지 않도록 모델이 궤적을 조정하게 합니다.
  • 충돌이 발생할 가능성이 있는 상황에서는 Repeller Cost가 높아져, 모델이 이를 피하도록 궤적을 변경하게 됩니다.

Repeller Cost 수식 이해하기

식 (15): Repeller Cost ( A )

A=max⁡((1−1rΔ(D(S;C,σ)))⊙(1−I),0)A = \max\left(\left(1 - \frac{1}{r} \Delta(D(S; C, \sigma))\right) \odot (1 - I), 0\right) (15)

  • 용어 해석:
    • ( A ): 각 시간 단계별로 계산되는 Repeller Cost.
    • ( r ): Repeller Radius. 두 에이전트 간 최소 허용 거리.
    • ( Δ(D(S;C,σ))\Delta(D(S; C, \sigma)) ): 모든 에이전트 쌍 간의 ( L_2 ) 거리를 계산한 결과. 크기는 ( RNa×Na×Nt\mathbb{R}^{N_a \times N_a \times N_t} )입니다.
    • ( I ): Identity Tensor. 자기 자신과의 거리는 항상 무시하도록 설정하기 위해 사용됩니다. 크기는 ( RNa×Na×Nt\mathbb{R}^{N_a \times N_a \times N_t} )입니다.
    • ( ⊙\odot ): 원소별 곱(Element-wise Multiplication).
    • (max⁡(⋅,0)\max(\cdot, 0)): 결과가 음수가 되지 않도록 하는 클램프 함수.

Repeller Cost 계산 과정:

  1. 거리 계산:

    • 모든 에이전트 쌍 간의 ( L_2 ) 거리를 계산하여 ( Δ(D(S;C,σ))\Delta(D(S; C, \sigma)) )를 구합니다.
    • 예: 에이전트 A와 B, A와 C, B와 C 간의 거리.

  2. 비교 및 비용 산출:

    • 각 거리에서 (1−1r×거리1 - \frac{1}{r} \times \text{거리} )를 계산합니다.
    • 이 값이 1보다 작으면 (즉, 거리가 ( r )보다 작으면), Repeller Cost가 발생합니다.
    • ( ⊙(1−I)\odot (1 - I) )는 자기 자신과의 거리는 고려하지 않도록 설정합니다.
    • 최종적으로, Repeller Cost ( A )는 ( (1−1rΔ)\left(1 - \frac{1}{r} \Delta \right) )가 양수인 경우에만 값을 가지며, 그렇지 않으면 0입니다.

식 (16): Repeller Loss ( Lrepell\mathcal{L}_{\text{repell}} )

Lrepell(D(S))=∑A∑(A>0)+eps\mathcal{L}_{\text{repell}}(D(S)) = \frac{\sum A}{\sum(A > 0) + \text{eps}} (16)

  • 용어 해석:

    • ( \sum A ): 모든 시간 단계에서의 Repeller Cost 합계.
    • ( \sum(A > 0) ): Repeller Cost가 0보다 큰 경우의 수(즉, 충돌이 발생한 에이전트 쌍의 수).
    • ( \text{eps} ): 작은 상수로, 분모가 0이 되는 것을 방지합니다.

  • Repeller Loss 계산 과정:

    • 모든 Repeller Cost를 합산한 값을, Repeller Cost가 발생한 경우의 수로 나눕니다.
    • 이는 평균 Repeller Cost를 계산하는 것과 유사합니다.
    • 모델은 이 손실을 최소화함으로써, 충돌을 피하는 궤적을 생성하도록 학습됩니다.

4.8. Constraint Score Thresholding (ST) (식 (17)과 (18))

Constraint Score Thresholding의 필요성

  • 안정성 유지: 제약 조건이 너무 강하게 작용하면 샘플링 과정이 불안정해질 수 있습니다.
  • 균형 유지: 확산 모델의 기본 점수 함수와 제약 점수 함수 간의 균형을 맞추어, 현실적이고 안전한 궤적을 생성합니다.

수식 이해하기

식 (17): 관계 설명

“(∇xlog⁡p(x;σ)=(D(x;σ)−x)σ2\nabla_x \log p(x; \sigma) = \frac{(D(x;\sigma) - x)}{\sigma^2})” (2) 에서 유도해보면,
σ∇xlog⁡p(x;σ)=D(x,σ)−xσ=ϵ,  ϵ∼N(0,I)\sigma \nabla_x \log p(x; \sigma) = \frac{D(x, \sigma) - x}{\sigma} = \epsilon, \; \epsilon \sim \mathcal{N}(0, I) (17)

  • 용어 해석:

    • ( σ\sigma ): 노이즈의 수준(표준편차).
    • ( ∇xlog⁡p(x;σ)\nabla_x \log p(x; \sigma) ): 점수 함수(데이터 분포의 로그 확률의 기울기).
    • ( D(x,σ)D(x, \sigma) ): 디노이저 함수. 노이즈가 섞인 데이터 ( x )를 깨끗한 데이터로 복원합니다.
    • ( ϵ\epsilon ): 표준 정규 분포를 따르는 노이즈 벡터.

  • 의미:

    • 점수 함수에 노이즈 수준 ( σ\sigma )를 곱하면, 디노이저가 예측한 노이즈 ( ϵ\epsilon )과 동일해집니다.
    • 이는 디노이저가 실제 노이즈를 얼마나 잘 예측하는지를 나타냅니다.
    • 이를 착안해서 식 (18)을 만들어봅시다.

식 (18): Constraint Score Thresholding

∇Slog⁡q(S;C,σ)  ≈  λ  ∂∂S  L(D(S;C,σ)).\nabla_S \log q(S;C,\sigma) \;\approx\; \lambda \;\frac{\partial}{\partial S}\; \mathcal{L}\bigl(D(S;C,\sigma)\bigr). (13) 참고

∇Slog⁡q(S;C,σ):=clip(σ∇Slog⁡q(S;C,σ),±1)/σ\nabla_S \log q(S; C, \sigma) := \text{clip}(\sigma \nabla_S \log q(S; C, \sigma), \pm 1)/\sigma (18)

  • 용어 해석:

    • ( ∇Slog⁡q(S;C,σ)\nabla_S \log q(S; C, \sigma) ): 제약 분포 ( q(S;C,σ)q(S; C, \sigma) )의 점수 함수.
    • clip((⋅\cdot), (±\pm 1)) : 입력 값을 (-1)에서 (+1) 사이로 제한하는 함수.
    • (/ \sigma): 노이즈 수준 ( \sigma )로 나누기.

  • 의미:

    • 제약 점수 ( ∇Slog⁡q\nabla_S \log q )를 (±1\pm 1) 사이로 제한하여, 너무 큰 값이 되지 않도록 합니다.
    • 이렇게 하면, 제약이 샘플링 과정에서 과도하게 영향을 미치는 것을 방지할 수 있습니다.
    • 노이즈 수준 ( σ\sigma )에 따라 제약 점수를 조정함으로써, 제약의 강도를 균형 있게 유지합니다.

4. Experiment and Results

4.2. Multi-Agent Motion Prediction

  • Waymo Open Motion dataset 에서 정의한 Metric을 차용함 (5가지)
  • multi(A마리)-agent 궤적 예측을 K개 한다고 하면, 우리는 K개 중, 가장 좋은 성능을 낸 궤적을 바탕으로 metric을 최종 도출합니다.
  • 3초, 5초, 8초 시간 기준의 각 metric 결과값을 각각 계산하였고, agent type(vehicles, pedestrians, cyclists) 마다 각각 계산했습니다.
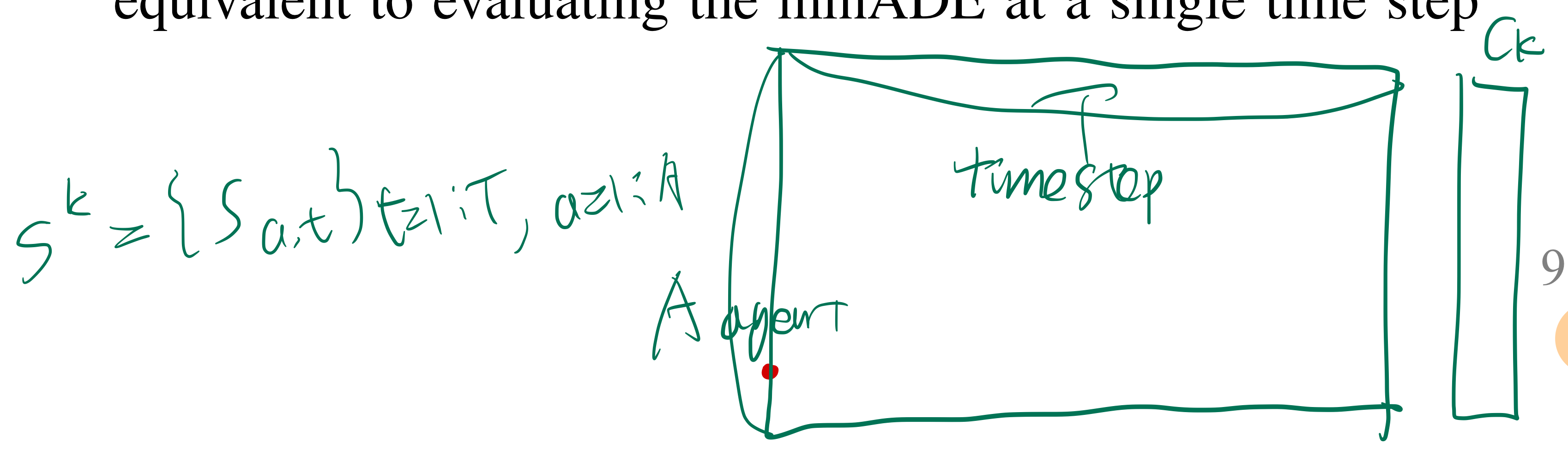
  • 위 그림의 c_k는 confidence score로 multi-agent 궤적 예측 1개당 -> 1개 scalar 값임

minSADE

  • minimum Average Displacement Error

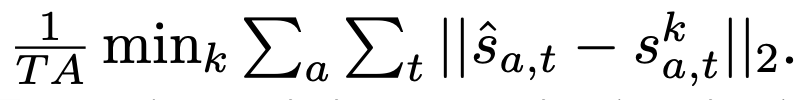
minSFDE

SMR

  • Miss Rate
  • IsMATCH(st^,st)IsMATCH({\hat{s_t}}, s_t): 시간 t의 각 waypoint에 대해, (모든 A마리 agent가) match인지 miss인지 표시하는 binary 값 (정답 궤적 위치와 가까운지 아닌지 판단)
    • MRt{MR}_{t} : 모든 A마리 agent가 전부 match되어야 match이고, 하나라도 miss이면, miss 입니다.
  • 그 time step에서의 miss rate는, dataset 전체에서 평균내서 계산합니다.
  • 우리는 속도가 느리거나, 예측 시간의 초반일수록 -> 더 빡빡한 match 기준을 세웁니다.
  • 그리고, lateral deviation과 longitudinal detivation의 threshold를 다르게 설정합니다.

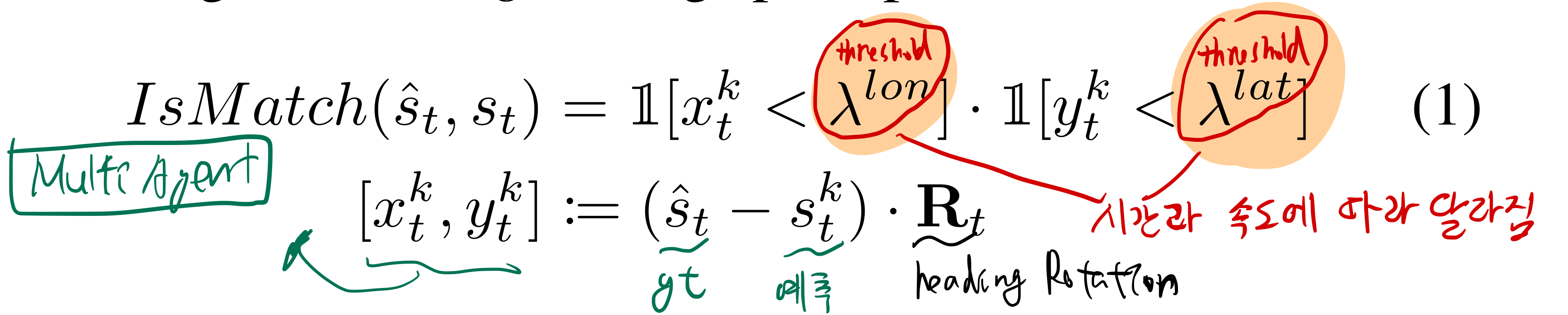
mAP

  • mean Average Precision
    • precision-recall curve의 아랫 면적 (by applying confidence score c_k threshold across a validation set)
      • 아마 예측한 K개 궤적 중, confidence score threshold를 넘는 궤적 후보군들만 남기고 TP, FP, FN 을 구분한다는 뜻 같다.
    • 더불어, 우리는 8개 다른 driving behavior (straight, straight-left, straight-right, left, right, left u-turn, right u-turn, and stationary) 에 대해 mAP를 각각 구한 후 평균했습니다.
  • Miss Rate를 이용해서 True Positive, False Positive, False Negative의 정의를 내림 (True Negative는 없음)
  • object detection분야? (예: 정답 2개, 예측 3개 상황에서, 정답-예측 IoU 기준 이상이 1개)
  • multi-agent trajectory prediction 분야?
    • K개 예측, 정답 1개
  • 논문 발췌
    • only one true positive is allowed for each object and is assigned to the highest confi- dence prediction, the others are counted as false positives.

True Positive

  • object detection분야: 1개
  • K개 예측 중, Miss Rate를 통과한 궤적들 중, 가장 confidence score가 높은 궤적 (1개)

False Positive

  • object detection분야: 2개
  • TP가 존재할 때, TP 를 제외한 나머지 궤적

False Negative

  • object detection분야: 1개
  • TP가 없을 떄, K개 궤적 예측 전부

Overlap metric

  • 가장 GT와 유사한 multi-agent trajectory가, 서로 경로끼리 얼마나 overlap 되는지를 측정한 매트릭
  • 좀 더 궁금하면 27 참조
profile
ad_official
ad_official

0개의 댓글