Tree

트리는 일반적으로 대상 정보의 각 항목들을 계층적으로 연관되도록 구조화시키고자 할 때 사용하는 비선형 자료구조이다.
데이터 요소들의 단순한 나열이 아닌 부모-자식 관계의 계층적 구조로 표현이 된다.
트리는 그래프의 한 종류이며 사이클이 없다.

용어

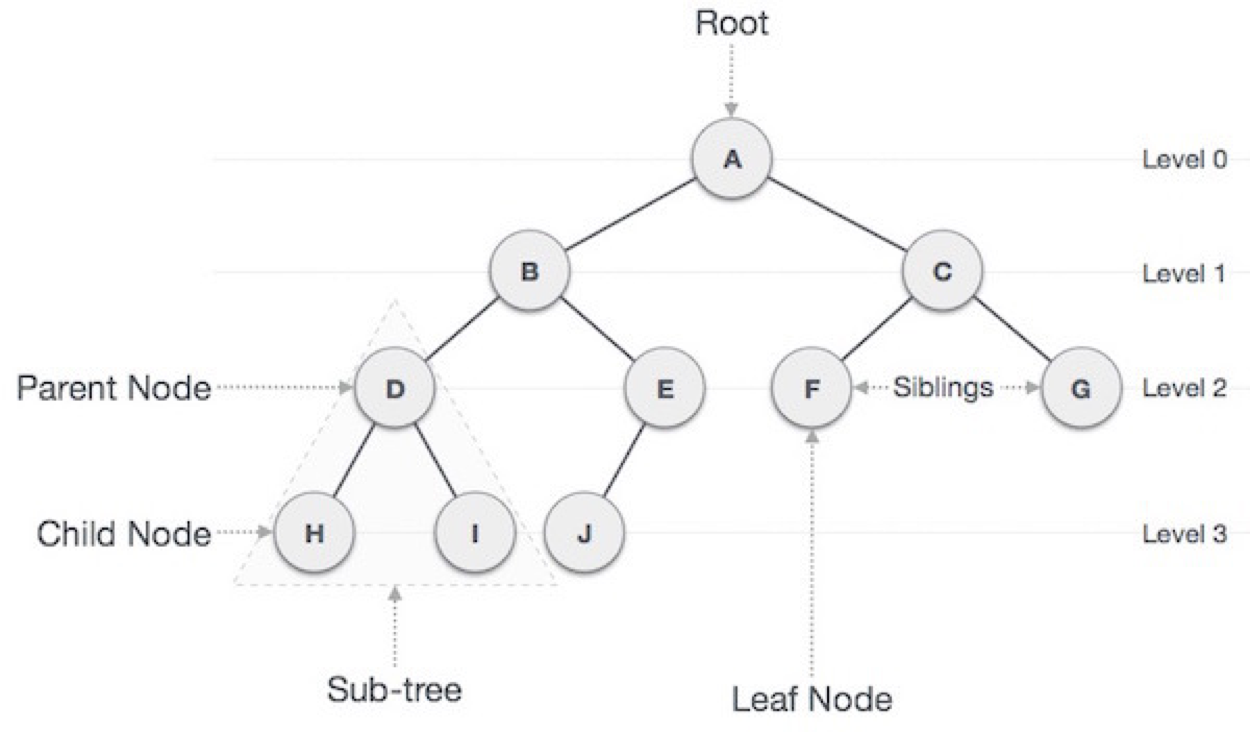
• node: 트리를 구성하고 있는 각 요소
• Edge(간선): 트리를 구성하기 위해 노드와 노드를 연결하는 선
• Root Node: 최상위 계층에 존재하는 노드
• level: 트리의 특정 깊이를 가지는 노드의 집합
• degree(차수): 하위 트리 개수 / 간선 수 (degree) = 각 노드가 지닌 가지의 수
• Terminal Node ( = leaf Node, 단말 노드) : 하위에 다른 노드가 연결되어 있지 않은 노드
• Internal Node (내부노드, 비단말 노드) : 단말 노드를 제외한 모든 노드로 루트 노드를 포함한다.

이진트리(Binary Tree)

이진트리는 트리를 구성하는 노드들의 최대 차수(degree)가 2인 노드들로 구성되는 트리이다.

• 이진트리의 레벨 i에서 가질 수 있는 최대 노드의 수는 2^i이다. (i>=0)
• 깊이가 k인 이진트리가 가질 수 있는 최대 노드의 수는 2^k-1이다.(k>=1)

이진트리는 완전 이진 트리(Completable Binary Tree)와 포화 이진 트리(Perfect Binary Tree), 전 이진 트리(Full Binary Tree)라고 하는 특별한 트리 구조를 정의할 수 있다.

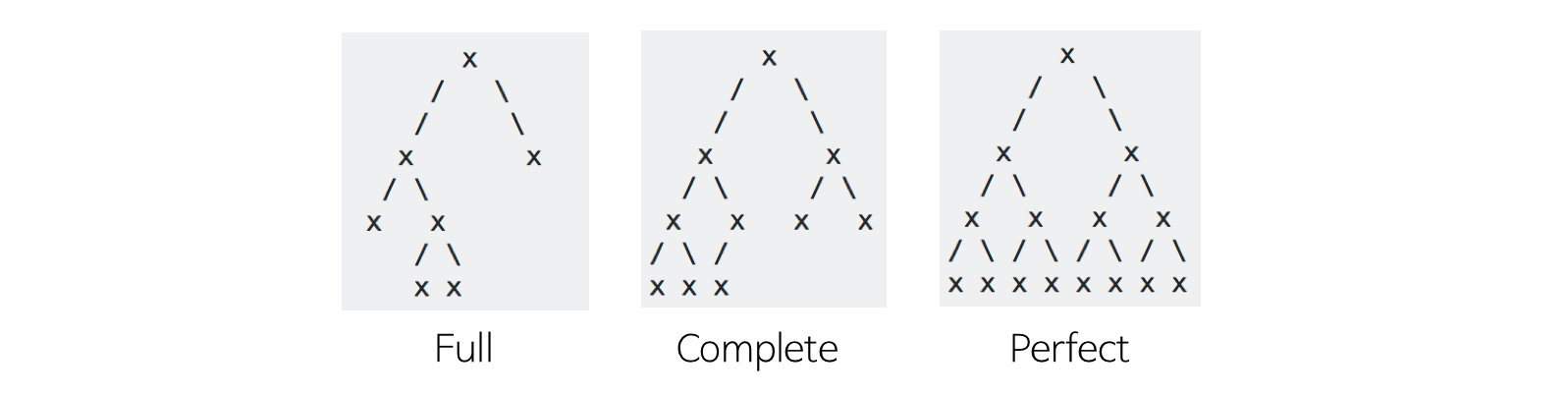
완전 이진 트리

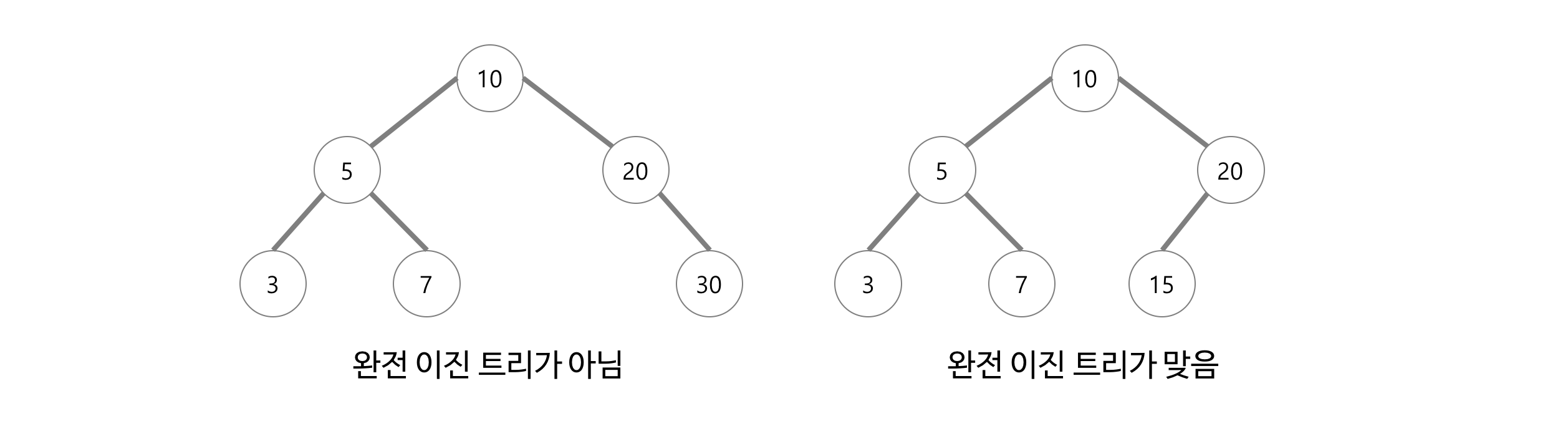
• 트리를 구성하고 있는 임의의 두 단말 노드의 레벨 차이가 1이하이고,
• 마지막 레벨을 제외한 모든 레벨에 존재할 수 있는 모든 노드를 갖고 있으며,
• 왼쪽에서 오른쪽으로 채워지는 이진트리
• heap

전 이진 트리

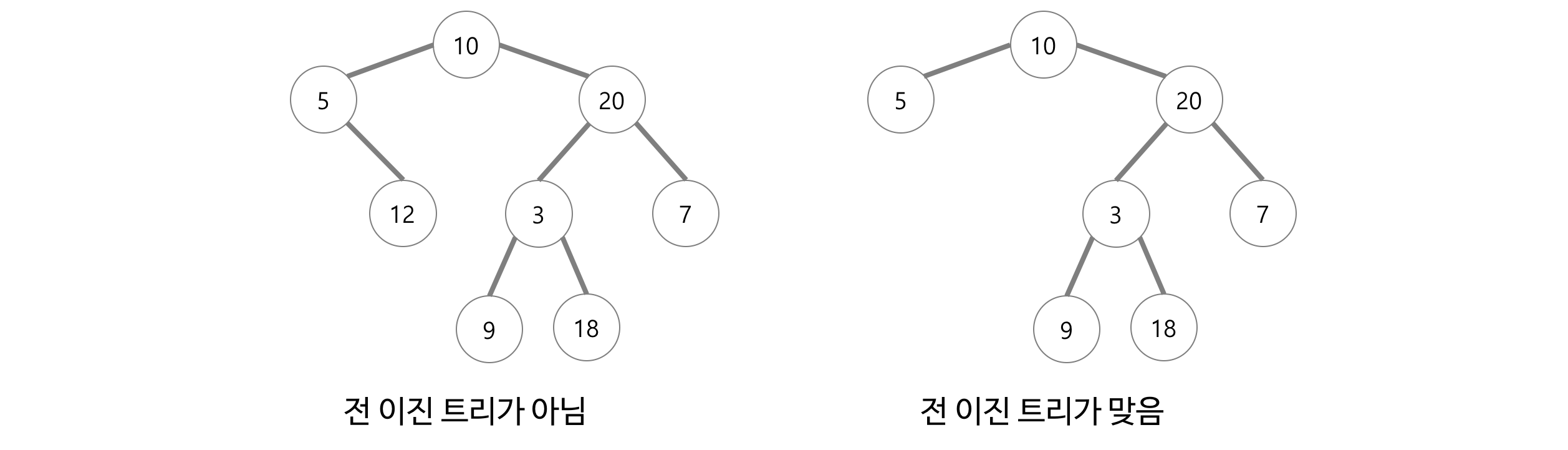
• 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리.

포화 이진 트리

• 모든 레벨에 노드가 차있는 상태로 최대 노드 수인 2^k-1개로 채워져 있는 트리
• 전 이진 트리이면서 완전 이진 트리인 경우

이진 트리의 표현

1. 배열을 이용한 표현

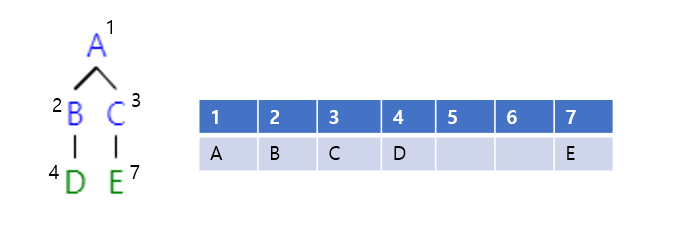
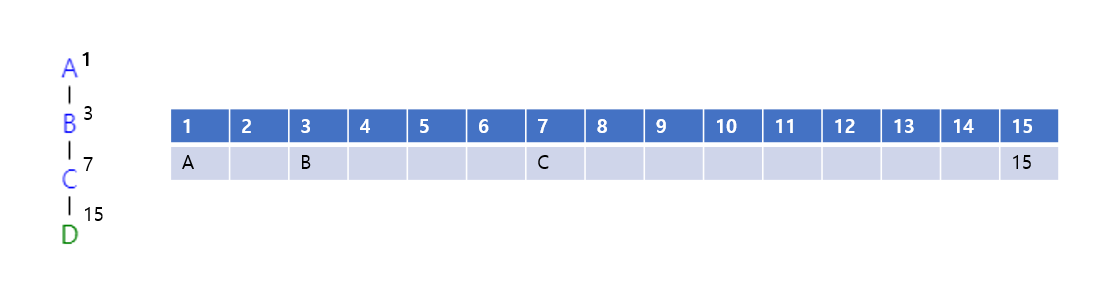
• 빈 노드에 대해서는 계속 사용하지 않기 때문에 메모리 낭비
• 데이터의 삽입, 삭제 연산시 노드의 레벨 변경으로 인한 데이터의 이동 발생

2. 연결리스트를 이용한 표현

• 각 노드는 data필드와 왼쪽 서브 트리를 가리키는 필드, 오른쪽 서브 트리를 가리키는 필드로 구성

이진 트리 순회

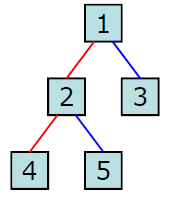
1. 중위 순회(inorder traversal)
왼쪽 서브트리 -> 루트 -> 오른쪽 서브트리
루트 노드가 가운데에 온다.
4-2-5-1-3
.
2. 후위 순회(postorder traversal)
왼쪽 서브트리 -> 오른쪽 서브트리 -> 루트
루트 노드가 후위에 온다.
4-5-2-3-1
.
3. 전위 순회(preorder traversal)
루트 -> 왼쪽 -> 오른쪽
루트 노드가 맨 앞에 온다.
1-2-4-5-3

이진 탐색 트리(Binary Search Tree)

모든 노드가 자신의 왼쪽 서브트리에는 현재노드보다 작은 키값이, 오른쪽 서브트리에는 현재 노드보다 큰 값이 오는 규칙을 만족하는 이진트리이다.

모든 왼쪽 자식들 <= n < 모든 오른쪽 자식들 (모든 노드 n에 대해서 반드시 참)
규칙 1. 이진 탐색 트리의 노드에 저장된 키는 유일하다.
규칙 2. 루트 노드의 키가 왼쪽 서브 트리를 구성하는 어떠한 노드의 키보다 크다.
규칙 3. 루트 노드의 키가 오른쪽 서브 트리를 구성하는 어떠한 노드의 키보다 작다.
규칙 4. 왼쪽과 오른쪽 서브트리도 이진 탐색 트리이다.

• 이진 탐색 트리의 탐색 연산은 평균 O(log n)의 시간 복잡도를 갖는다.
• 비교적 삽입, 삭제가 효율적인 자료구조이다.
• 이진 탐색 트리는 Skewed Tree(편향 트리)가 될 수 있다.
  • 저장 순서에 따라 계속 한 쪽으로만 노드가 추가되는 경우가 발생하기 때문.(O(n))
  • 이를 해결하기 위해 균형잡힌 이진검색트리를 고안. 대표적인 것은 레드블랙트리와 AVL트리다.
• 이진 탐색 트리는 이진 탐색을 쉽게 할 수 있도록 만들어진 트리이다.

Red-Black Tree

레드블랙 트리는 자가균형이진탐색 트리(self-balancing binary search tree)로써, 대표적으로 연관배열(associative array) 등을 구현하는데 쓰이는 자료구조이다.

특징

balanced binary search tree

• 이진 탐색 트리가 편향 트리가 될 경우를 방지하는 조건을 추가함
  • 균형이 잡혀 위 그림 같은 경우가 안나온다 -> 레드블랙트리의 높이는 logn에 바운드 된다 -> 레드블랙트리에서 삽입, 삭제, 검색 연산은 O(logn)의 시간복잡도를 가지게 된다.
• 자료의 삽입과 삭제, 검색에서 최악의 경우에도 일정한 실행 시간을 보장한다(worst-case guarantees).
  • 이는 실시간 처리와 같은 실행시간이 중요한 경우에 유용하게 쓰일 뿐만 아니라, 일정한 실행 시간을 보장하는 또 다른 자료구조를 만드는 데에도 쓸모가 있다. 예를 들면, 각종 기하학 계산에 쓰이는 많은 자료 구조들이 레드-블랙 트리를 기반으로 만들어져 있다.

조건

1. Root Property : 루트노드의 색깔은 검정(Black)이다.
   (추가되는 노드는 빨강이다)
2. External Property : 모든 external node들은 검정(Black)이다.
3. Internal Property : 빨강(Red)노드의 자식은 검정(Black)이다.
   == No Double Red(빨간색 노드가 연속으로 나올 수 없다.)
4. Depth Property : 모든 리프노드에서 Black Depth는 같다.
   == 리프노드에서 루트노드까지 가는 경로에서 만나는 블랙노드의 개수는 같다.
   (그냥 노드의 수는 다를 수 있음.)

위 조건들을 만족하게 되면, 레드블랙 트리는 가장 중요한 특성을 나타내게 된다. 루트 노드부터 가장 먼 경로까지의 거리가, 가장 가까운 경로까지의 거리의 두 배보다 항상 작다. 다시 말해 레드블랙 트리는 개략적으로 균형이 잡혀있다. 따라서, 삽입, 삭제, 검색 시 최악의 경우(worst-case)에서의 시간복잡도가 트리의 높이(깊이)에 따라 결정되기 때문에 보통의 이진검색 트리에 비해 효율적이다.

Double Red 해결 전략

이렇게 연속해서 빨강 노드가 오게 되었을 때 해결 방법은 두가지 이다.

현재 insert된 노드의 uncle node(부모 노드의 형제 노드)를 w라고 할때,

• w==Black 👉 Restructuring
• w==Red 👉 Recoloring

즉, insert노드의 uncle node의 색을 기준으로 해결 전략이 달라지게 된다.

Restructing
1. 나(z)와 내 부모(v), 내 부모의 부모(Grand Parent)를 오름차순으로 정렬
2. 무조건 가운데 있는 값을 부모로 만들고 나머지 둘을 자식으로 만든다.
3. 올라간 가운데 있는 값을 검정(Black)으로 만들고 그 두자식들을 빨강(Red)로 만든다.

• Restructuring은 다른 서브트리에 영향을 끼치지 않기 때문에(4번조건) 한번의 과정으로 종료.
  • Restructing 전후의 Black 노드의 개수에 변화가 없기때문에 다른서브트리에 영향을 끼치지 않음
• Restructuring자체의 시간복잡도는 O(1)에 끝나지만, (순서결정시간 - 상수시간, 트리로 만드는시간 - 상수시간, 원래있던 노드들의 구조들을 바꿔주는 시간 - 상수시간)
  Restructuring은 어떤 노드를 insertion한 뒤 일어나므로 총 수행시간은 O(logn)이다. 지금 현재 노드가 들어갈 위치를 먼저 찾아야 하기 때문.

Recoloring
1. 현재 insert된 노드(c)의 부모(p)와 그 형제(u)를 검정(Black)으로 하고 Grand Parent(내 부모의 부모)를 빨강(Red)로 한다.
2. Grand Parent(내 부모의 부모)가 Root node가 아니었을 시 Double Red가 다시 발생 할 수 있다.

• Recoloring의 경우 Restructuring과 다르게 propagation될 수 있다. 최악의경우 Root까지 갈 수 있음.

AVL Tree와 Red Black Tree 차이

• AVL Tree가 Red Black Tree보다 빠른 Search를 제공
  • AVL Tree가 더 엄격한 Balanced를 유지하고 있기 때문
• Red Black Tree은 AVL Tree보다 빠른 삽입과 제거를 제공
  • AVL Tree보다 Balanced를 느슨하게 유지하고 있기 때문
• Red Black Tree는 AVL Tree보다 색깔을 저장하기 위해 더 많은 Space Complexity가 필요
• Red Black Tree는 대부분의 언어의 map, multimap, multiset에서 사용
• AVL tree는 조회에 속도가 중요한 Database에서 사용

Heap

힙(heap)은 완전이진트리(Complete binary tree) 를 기본으로 한 자료구조(tree-based structure) (시간복잡도 : O(log N))

특징

• 일반적으로 배열을 사용하여 구현한다.배열에 트리의 값들을 넣어줄 때, 0 번째는 건너뛰고 1 번 index 부터 루트노드가 시작된다.
• 여러 개의 값들 중에서 최댓값이나 최솟값을 빠르게 찾아내도록 만들어진 자료구조이다. (우선순위큐 구현시 사용함)
• 힙은 일종의 반정렬 상태(느슨한 정렬 상태) 를 유지한다.
  • 큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있다는 정도
  • 간단히 말하면 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰(작은) 이진 트리를 말한다.
• 힙 트리에서는 중복된 값을 허용한다. (이진 탐색 트리에서는 중복된 값을 허용하지 않는다.)

힙의 종류

최대 힙

부모노드의 키값이 자식노드의 키값보다 항상 큰 힙
Max Heap에서는 Root node 에 있는 값이 제일 크므로, 최대값을 찾는데 소요되는 연산의 time complexity 이 O(1)이다. 그리고 complete binary tree이기 때문에 배열을 사용하여 효율적으로 관리할 수 있다. (즉, random access 가 가능하다. Min heap 에서는 최소값을 찾는데 소요되는 연산의 time complexity 가 O(1)이다.)

최소 힙

부모노드의 키값이 자식노드의 키값보다 항상 작은 힙
키값의 대소관계는 부모-자식 간에만 성립하고 형제간에는 성립하지 않는다.

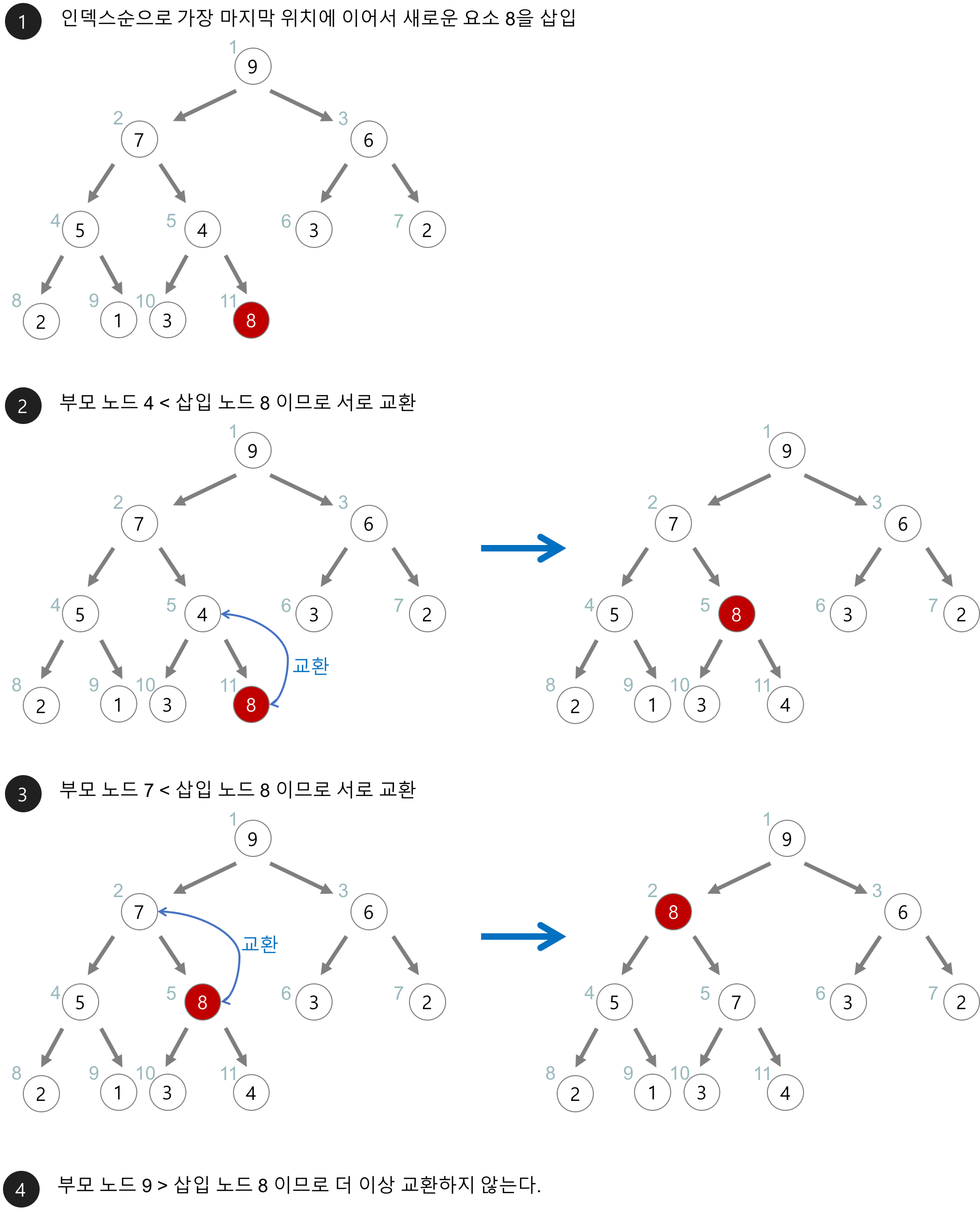
삽입

(max heap 기준)
1. 힙의 가장 마지막 원소에 원하는 값을 삽입한다.
2. 부모가 삽입 원소보다 작다면(Max_Heap기준) 부모와 자식의 값을 교환한다.
3. 2번에서 부모가 없거나, 부모가 자식보다 클 경우에 종료

삭제

(max heap 기준)
1. 루트노드를 삭제하고 힙의 마지막 노드를 루트로 가져온다.
2. 가져온 루트와 자식노드를 비교하고 가져온 노드가 작을 경우 자식과 위치 변경
3. 자식 노드가 더이상 없거나, 자식보다 클 경우 종료

---

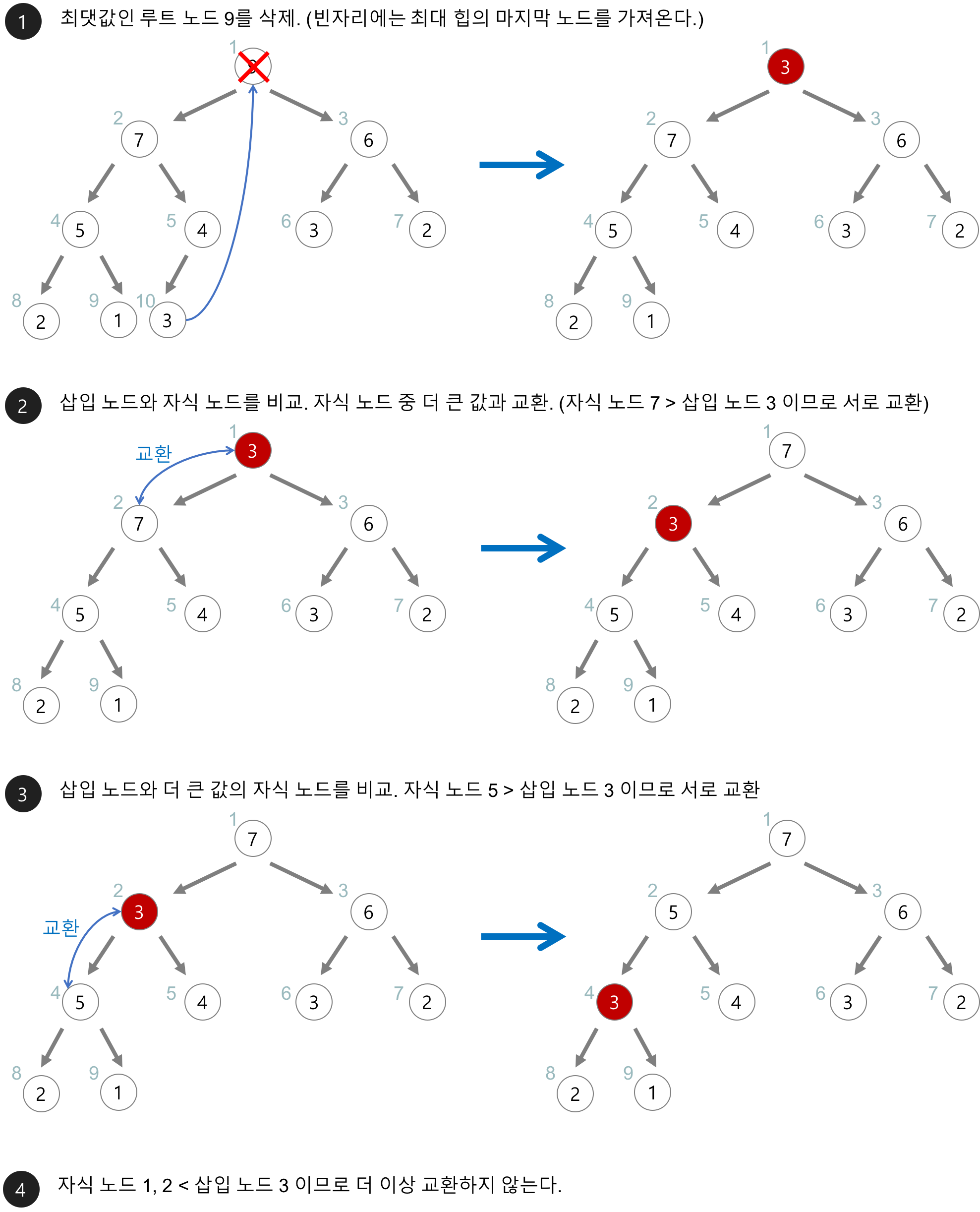
참고
https://gmlwjd9405.github.io/2018/08/12/data-structure-tree.html
https://wayhome25.github.io/cs/2017/04/19/cs-23/
https://coderkoo.tistory.com/10
https://zeddios.tistory.com/237
https://nesoy.github.io/articles/2018-08/Algorithm-RedblackTree