How does Normalization help DNN training?

• Stabilizing Activation Distributions
• Faster Convergence
• Regularization
• Enabling Larger Learning Rates
• Reducing Internal Covariate Shift
• Making Networks Robust to Initialization
• Reducing Gradient Vanishing/Exploding

Batch Normalization

A mechanism that aims to stabilize the distribution over a mini-batch of inputs to a given network layer during training.

• augment the network w/ additional layers that set mean&variance of the distribution of each activation to be zero and one respectively.
• batch normalized inputs can be scaled and shifted based on trainable parameters to preserve model expressivity.
• applied before non-linearity of previous layer

What is the benefit?

Faster Convergence

BatchNorm reduces internal covariate shift, which leads to more stable gradients and faster convergence during training. This can lead to shorter training times and require fewer training epochs.

→ makes the landscape of the corresponding optimization problem
significantly smooth :

• ensure that gradients are more predictive → gradient direction remains fairly accurate when taking larger step in a direction of a computed gradient

• allows for use of larger range of learning rates and faster network convergence

• improved Lipschitzness(ß-smoothness) of both the loss & gradients

↔ non-convex, flat region, sharp minima

• convex 함수의 경우, 우리가 딥러닝에서 경사 하강법을 통해 찾는 최저점이 단 하나 존재한다. 이 점을 전역 최적해Global Minimum이라고 한다.
• non-convex 함수는 무한히 넓은 함수 공간에서 여러 곳의 지역 최저점 Local minima을 갖는다. 위 함수에서 이로 인하여, 경사 하강법을 시작하는 위치에 따라 서로 다른 최저점을 향해 결과가 수렴하게 된다. non-convex 함수의 문제는 우리가 어디가 전역 최적해인지를 알 수가 없다는 것이다. 이로 인해 non-convex 한 문제를 딥러닝으로 해결하려고 하면 학습이 잘 되지 않고 좋지 않은 지역 최저점에 갇히는 등의 문제가 발생한다.

• ICS : the change in the distribution of layer inputs caused by updates to the preceding layers.

Regularization:

BatchNorm acts as a form of regularization, reducing the need for other regularization techniques like dropout. It can mitigate overfitting to some extent.

Increased Learning Rates

BatchNorm allows for the use of higher learning rates without the risk of causing divergence or instability in the training process.

Network Robustness

BatchNorm can make neural networks more robust to changes in initialization and architecture choices. less sensitive to hyperparameter choices

Prevention of exploding or vanishing gradients

Layer Normalization

Layer normalization works well for RNNs and improves both the training time and the generalization performance of several existing RNN models.

Batch Norm in RNN can be problematic because we need to compute and store separate statistics for each time step in a sequence & when the length of sequence is different for test cases. On the other hand, Layer Norm depend only on the summed inputs to a layer at the current time-step & has only one set of gain and bias parameters shared over all time-steps.

In Layer Norm, all the hidden units in a layer share the same normalization terms µ & σ but different training cases have different normalization terms. ‘covariate shift’ problem can be reduced by fixing the mean, variance of the summed inputs in the same layer:

According to Xiong et.al

1. learning-rate warm up stage is essential ?

   Original-designed Post-LN Transformer places the layer normalization between the residual blocks
   → expected gradients of the parameters near the output layer are large
   → Using large learning rate on the gradients make training unstable

2. location of layer normalization matters ?

   If the layer-normalization is put inside the residual blocks
   (Pre-LN Transformer), the gradients are well-behaved at initialization

   → remove warm up stage

Instance Normalization

started from real-time image generation / style transfer

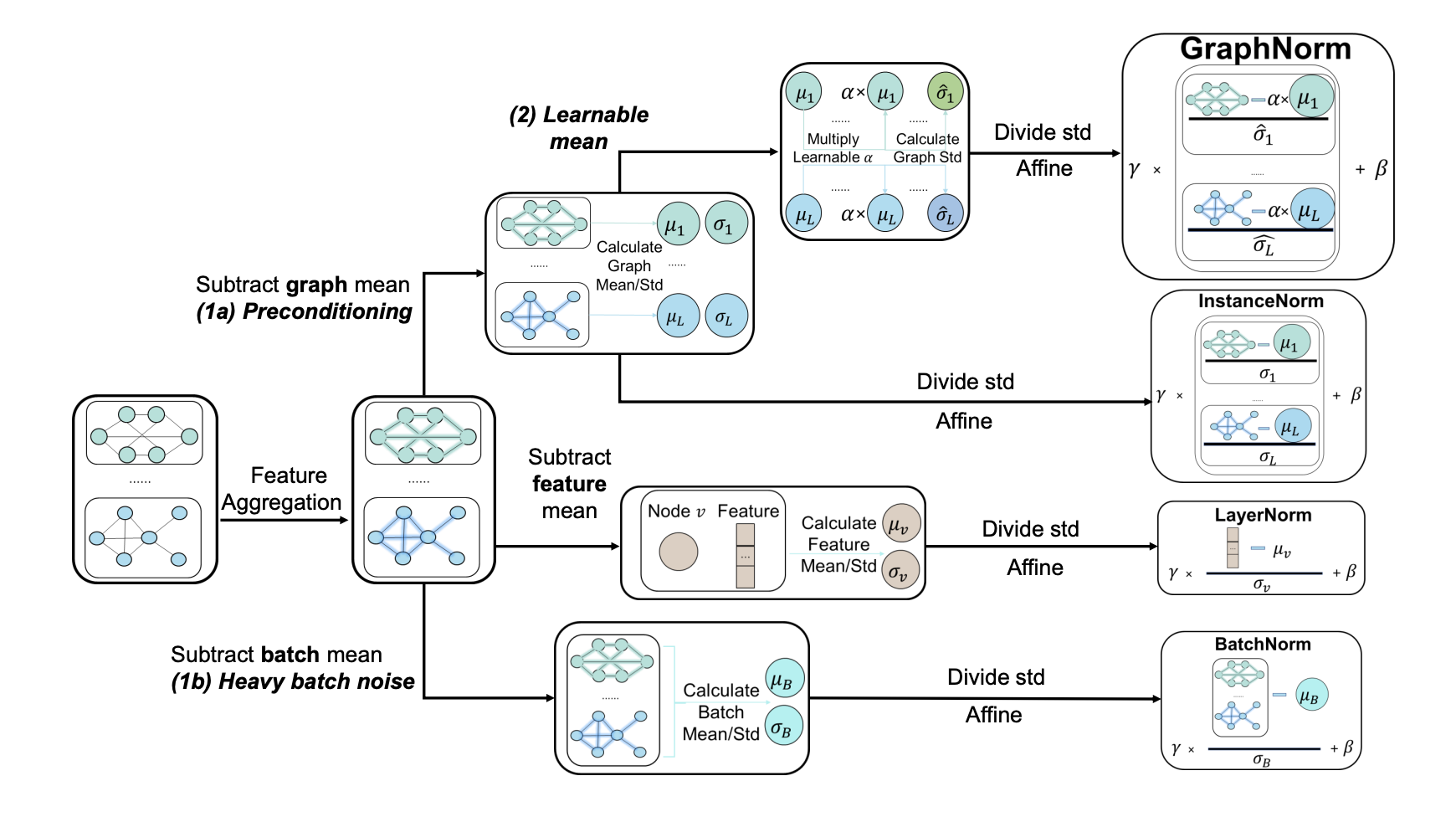
Graph Normalization

Instance Norm serves as a pre-conditioner(for graph aggregation) for GNNs.
Preconditioning is weaker with Batch Norm due to heavy batch noise in graph dataset : larger variance of batch-level statistics on graph dataset .
Shift operation in Instance Norm(subtracts the mean statistics from node hidden representations) has expressiveness degradation of GNNs for highly regular graphs - removing mean statistics that has structural information can hurt the performance

Representation of normalization layer(after the linear transformation)

$H^{(k)} = F^{(k)}(Norm(W^{(k)}H^{(k-1)}Q))$

$F^{(k)}$ : function that applies to each node separately

$Q$ : $n*n$ matrix representing the neighbor aggregation

$W^{(k)}$ : weight/parameter matrix in layer k

• $F^{(k)}$ : ReLU , $Q_{GCN}$ → GCN with normalization
• $F^{(k)} : MLP^{(k)}$, $Q_{GIN}$ → GIN with normalization

---

Reference

Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
Layer Normalization
Instance Normalization: The Missing Ingredient for Fast Stylization
GraphNorm: A Principled Approach to Accelerating Graph Neural Network Training
On Layer Normalization in the Transformer Architecture