[Unit 1] Graph

Graph

Graph
여러 개의 점이 서로 복잡하게 연결된 관계를 표현한 자료구조
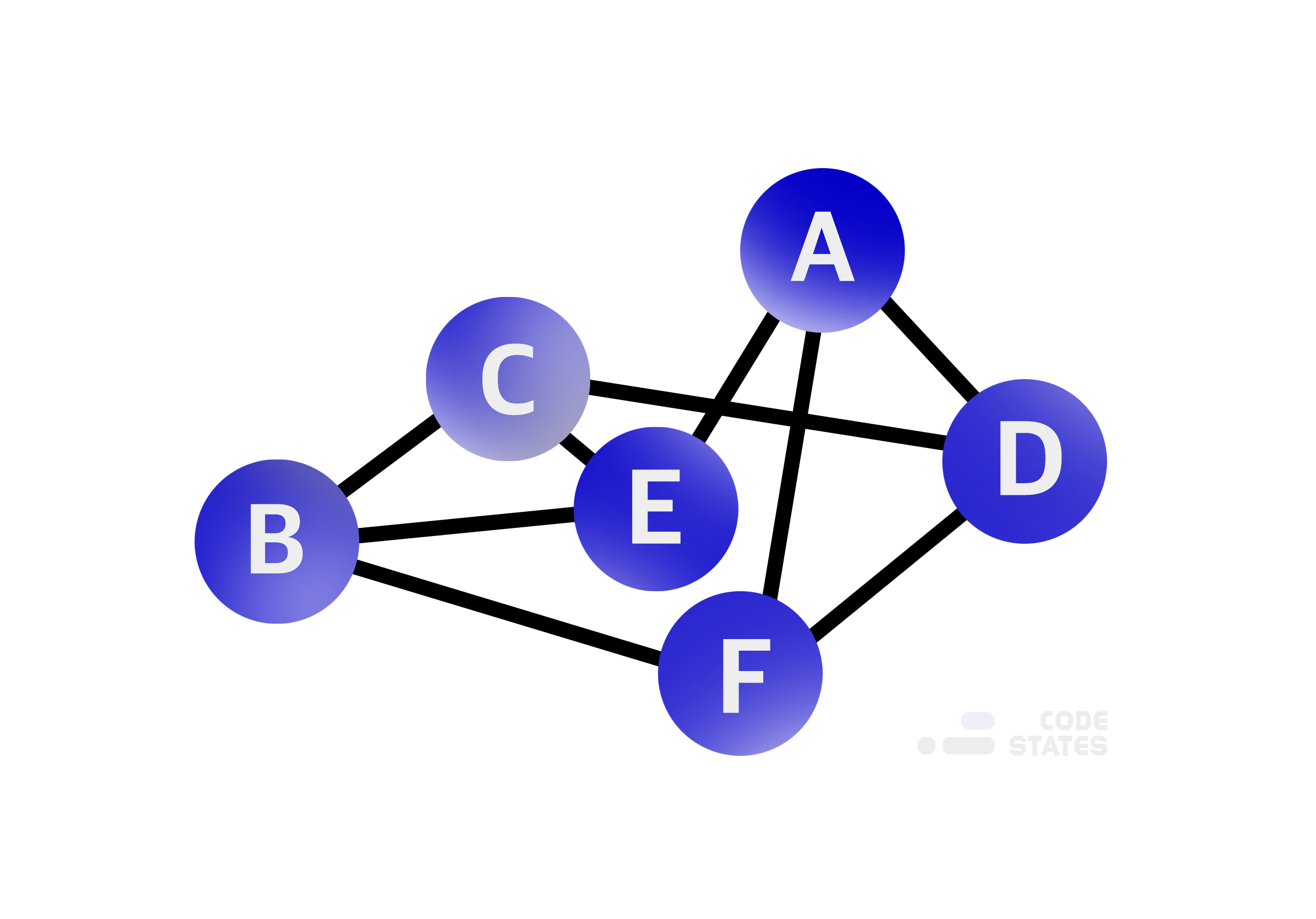
Graph의 구조

• 직접적인 관계가 있는 경우 두 점 사이를 이어주는 선이 있다.
• 간접적인 관계라면 몇 개의 점과 선에 걸쳐 이어진다.
• 하나의 점을 그래프에서는 정점(vertex) 이라고 표현하고, 하나의 선은
  간선(edge) 이라고 한다.
  
• 정점(vertex) : 노드(node)라고도 하며 데이터가 저정되는 그래프의 기본 원소
• 간선(edge) : 정점 간의 관계 (정점을 이어주는 선)
• 인접 정점(adjacent vertex) : 하나의 정점에서 간선에 의해 직접 연결된정점
• 가중치 그래프(weighted Graph) : 연결이 강도가 얼마나 되는지 적혀 있는 그래프
• 비 가중치 그래프(unweighted Graph) : 연결의 강도가 적혀 있지 않은 그래프
• 무방향 그래프(undirected graph) : 서울에서 부산으로 갈수 있듯, 부산에서 서울로 가는 것도 가능
• 단방향 그래프(directed graph) : 서울에서 부산으로 갈수 있지만 부산에서 서울로 가는 것은 불가능
• 진입차수(in-degree)/진출차수(out-degree) : 한 정점에 진입하고 진출하는 간선이 몇개인지를 나타냄
• 인접(adjacency) : 두 정점 간에 간선이 직접 이어져 있으면 두 정점은 인접한 정점
• 자기 루프(self loop) : 정점에서 진출하는 간선이 곧바로 자기 자신에게 진입하는 경우, 다른 정점을 거치지 않음
• 사이클(cycle) : 한정점에서 출발해 다시 해당 정점으로 돌아갈 수 있으면 사이클이 있다고 표현 서울 - 대전- 부산 - 서울
  
  
  Graph 표현 방식
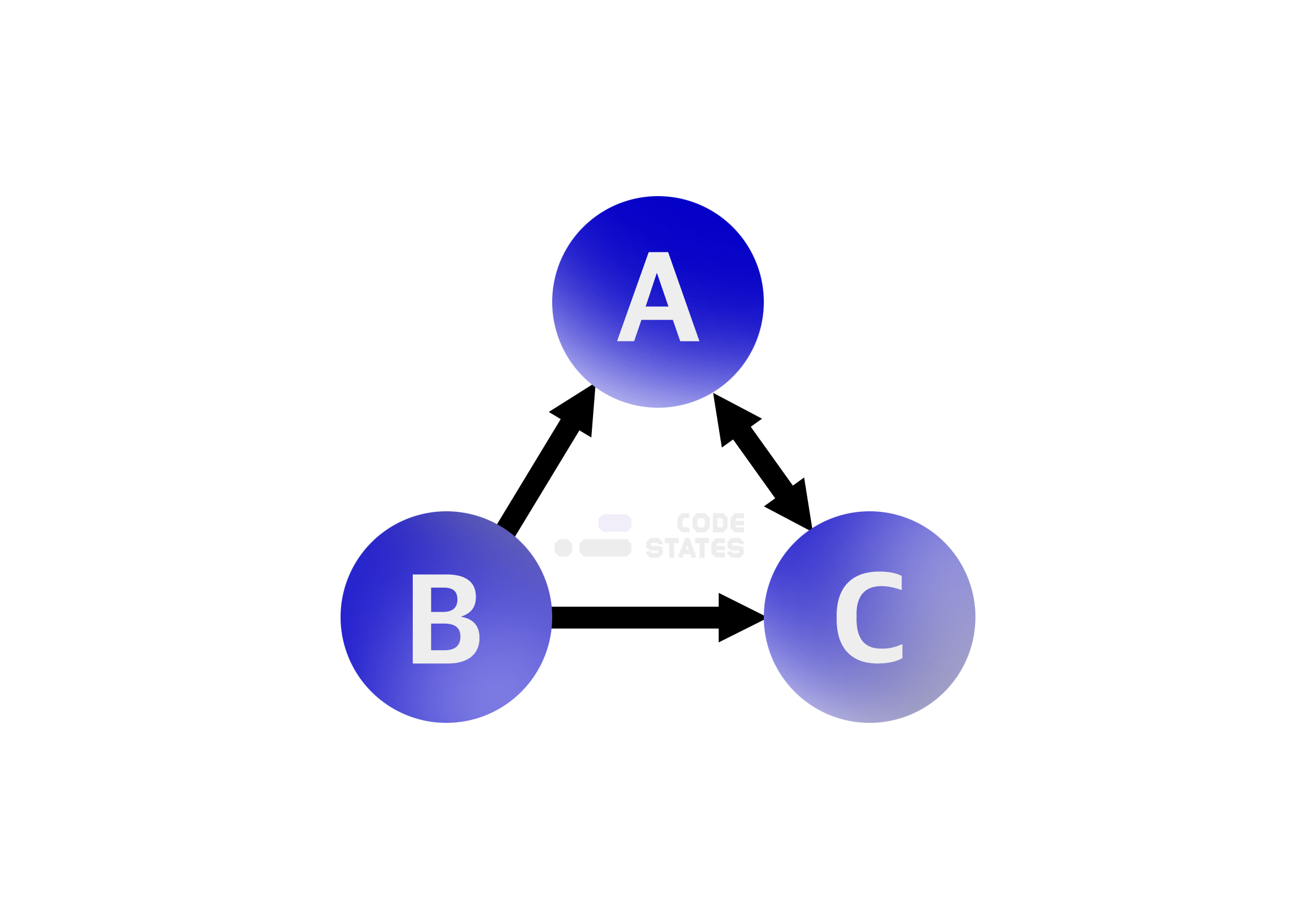
  인접 행렬
  두 정점을 바로 이어주는 간선이 있다면 두 정점은 인접하다고 한다.
  두 정점이 이어져 있다면 1(true), 이어지지 않았다면 0(false)로 표시

A의 진출차수는 1개입니다: A —> C
[0][2] === 1 // A([0])는 C([2])로 가는 진출차수가 있다(1)
B의 진출차수는 2개입니다: B —> A, B —> C
[1][0] === 1 // B([1])는 A([0])로 가는 진출차수가 있다(1)
[1][2] === 1 // B([1])는 C([2])로 가는 진출차수가 있다(1)
C의 진출차수는 1개입니다: C —> A
[2][0] === 1 // C([2])는 A([0])로 가는 진출차수가 있다(1)

인접 리스트
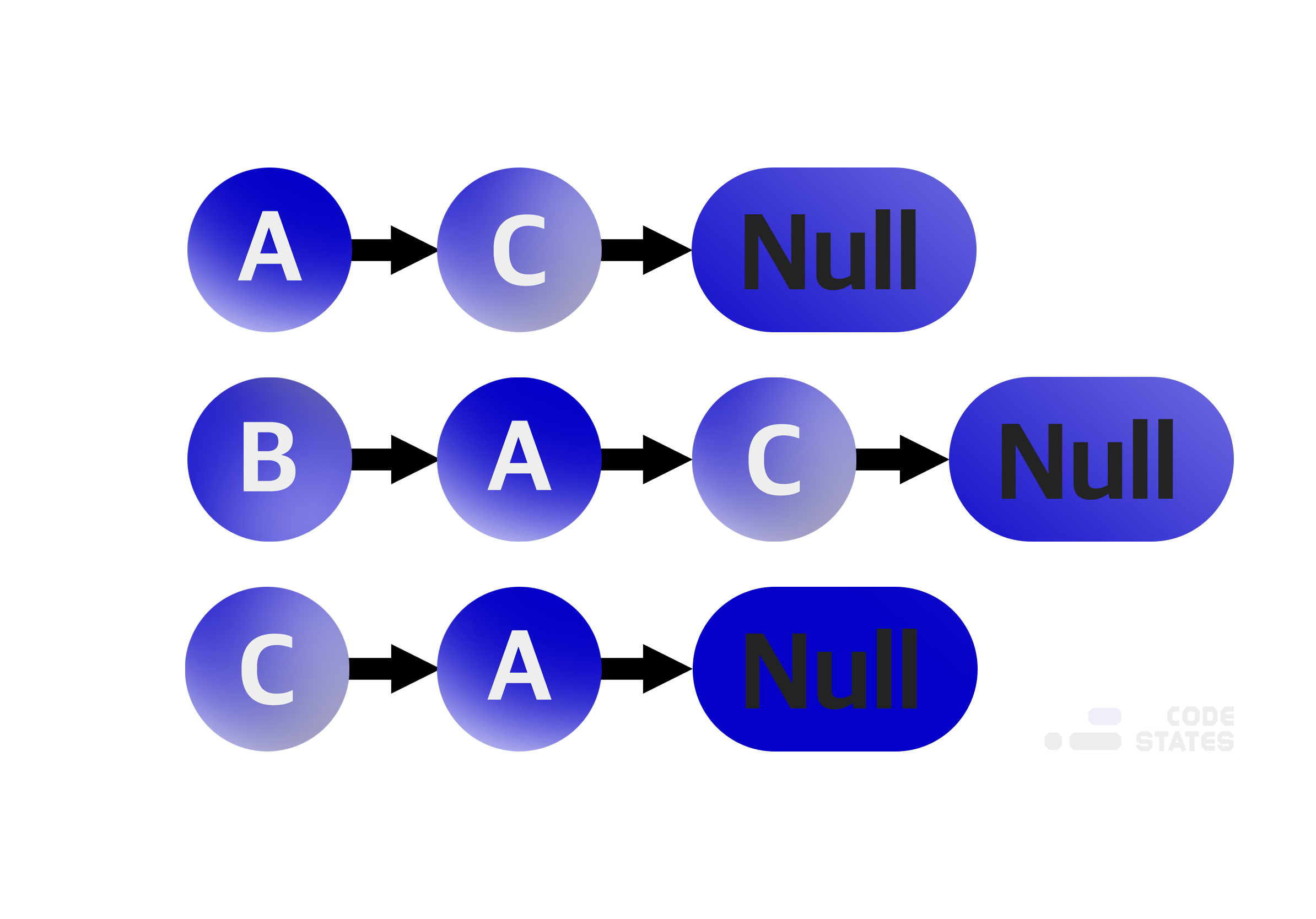
각 정점이 어떤 정점과 인접하는지를 리스트 형태로 표현
각 정점마다 하나의 리스트를 가지고 있고 이 리스트는 자신과 인접한 정점을 담고 있다.
인접행렬과 인접 리스트 사용

[인접 행렬]
1. 한 개의 큰 표와 같은 모습을 한 인접 행렬은 두 정점 사이에 관계가 있는지, 없는지 확인하기에 용이합니다.
    - 예를 들어, A에서 B로 진출하는 간선이 있는지 파악하기 위해선 0번째 줄의 1번째 열에 어떤 값이 저장되어있는지 바로 확인할 수 있습니다.
2. 가장 빠른 경로(shortest path)를 찾고자 할 때 주로 사용됩니다.
    - 최단 경로를 구하는 과정(BFS)에서는 그래프 탐색이 빈번하게 발생하는데, 이때 인접행렬이 인접리스트에 비해 조회 성능이 우수합니다. 
인접행렬의 경우 인덱스를 직접 접근하여 조회가 O(1)로 이루어지기 때문입니다. 
반면, 인접리스트의 경우 각 row를 선형 조회해야 하므로 노드의 수가 N일 경우 O(N)의 시간이 소요됩니다.
정리하자면, 인접리스트의 경우 A 노드에서 B 노드로 이동하는 경우만 해도 O(N)의 시간이 소요되며, 더불어 최단 경로를 구하는 과정 자체에서도 시간이 많이 소요되기 때문에 
인덱스를 통한 직접 접근이 가능한 인접행렬이 최단경로를 찾는 데 더 유리한 측면이 있다는 것입니다.
[인접 리스트]
1. 메모리를 효율적으로 사용하고 싶을 때 인접 리스트를 사용합니다.
    - 인접 행렬은 연결 가능한 모든 경우의 수를 저장하기 때문에 상대적으로 메모리를 많이 차지합니다.

DFS & BFS

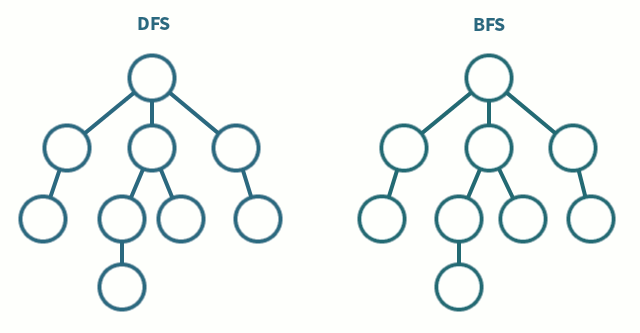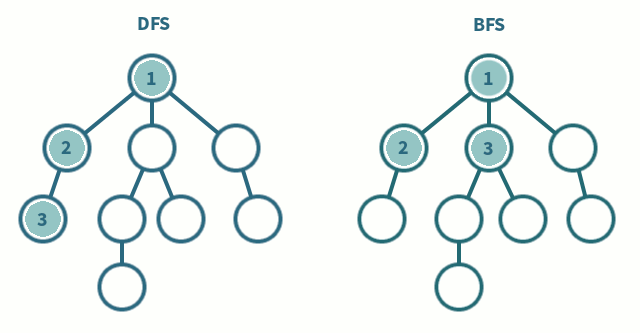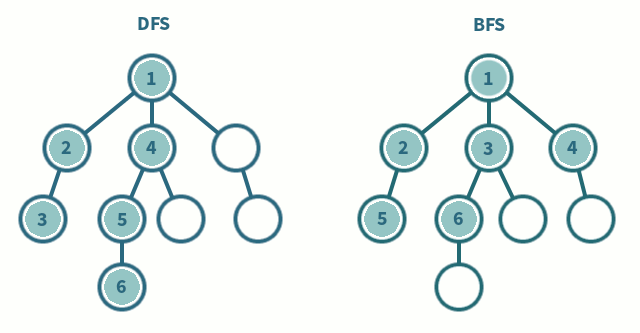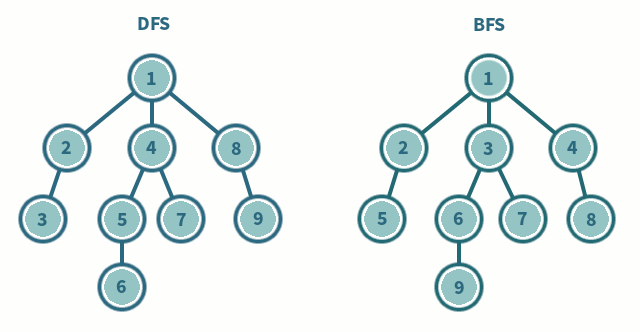
깊이 우선 탐색(DFS;Depth-First Search)
로트노드에서 시작해 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방식
최대한 깊이 내려간 뒤, 더이상 깊이 갈 곳이 없을 경우 옆으로 이동

• 모든 노드를 방문하고자 하는 경우
• DFS가 BFS보다 좀 더 간단
• 검색 속도 자체는 BFS에 비해 느림
  
  
  너비 우선 탐색(BFS; Breadth-First Search)
  루트노드에서 시작해 인접한 노드를 먼저 탐색하는 방법
  최대한 넓게 이동한 다음, 더이상 갈 수 없을때 아래로 이동
• 최단 경로를 찾고 싶은 경우

내용 참조, 이미지 출처 : 코드스테이츠
DFS,BFS 이미지 출처 :https://devuna.tistory.com/32