깊이 우선 탐색 (Depth-first search, DFS)

깊이 우선 탐색

DFS 역시 BFS와 마찬가지로 그래프를 탐색하는 알고리즘의 하나로, 시작 정점으로부터 하나의 방향을 잡아 끝까지 탐색한 후 마지막 분기점으로 돌아와 다시 다른 방향으로 끝까지 탐색을 반복하는 방식이다. 이렇게 이름처럼 깊이를 우선적으로 쭉 탐색하기 때문에 그래프의 최대 경로가 정해져 있거나, 깊이를 예측할 수 있는 경우에 사용된다.

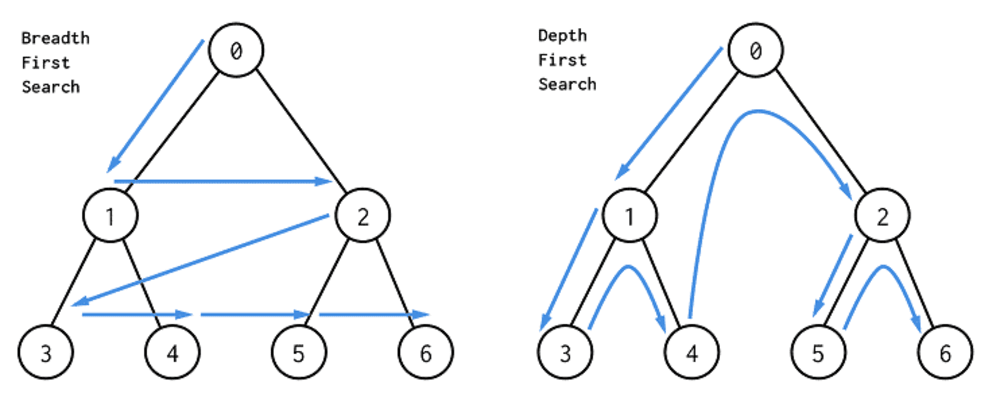※ 이미지 출처 : https://dev.to/danimal92/difference-between-depth-first-search-and-breadth-first-search-6om

DFS 구현 : 스택 / 재귀함수

더 이상 방문할 정점이 없을 때 마지막 분기점으로 돌아오는 로직은 스택을 이용하거나 재귀함수를 이용해 구현할 수 있다.
이 경우에도 BFS와 같이 한 정점을 두 번 방문하는 일이 없도록 방문 여부를 나타내는 리스트를 따로 만들어 두고, 정점을 방문할 때 마다 방문 표시를 해둔다.

DFS 알고리즘

• 스택을 활용한 DFS

  1. 시작 정점을 스택에 삽입한다.
  2. 스택에서 하나의 정점을 꺼낸다.
  3. 스택에서 꺼낸 정점이 아직 방문하지 않은 정점이라면, 방문 표시 후 이웃 정점들을 스택에 삽입한다.
  4. 스택에 담긴 정점이 없을 때까지 2-3번 과정을 반복한다.

• 재귀함수를 활용한 DFS

  1. 파라미터로 넘어온 정점이 이미 방문한 정점일 경우 return 하도록 base condition을 설정한다.
  2. 파라미터로 넘어온 정점이 방문하지 않은 정점일 경우 방문 표시를 한다.
  3. 인접 정점에 대해 재귀적으로 함수를 호출하며 탐색을 진행한다.

DFS 코드 (Python)

# 그래프 탐색 (DFS)

# 1) 스택을 이용한 DFS 구현
def dfs_stack(graph, start):
    visited = []
    stack = []
    
    # 시작 노드 스택에 담기   
    stack.append(start)
    
    # 스택에 방문하지 않은 인접 정점들을 담은 후 하나씩 빼오면서 탐색
    while stack:
        now = stack.pop()
        if now not in visited: 
            visited.append(now)
            stack.extend(graph[now])

    return ' '.join(visited)


# 2) 재귀함수를 이용한 DFS 구현
visited = []
def dfs_recursive(graph, start):
    # 이미 방문한 노드라면 탐색 종료
    if start in visited:
        return
    
    # 방문 표시
    visited.append(start)
    print(start, end=' ')

    # 인접 정점들에 대해 재귀 호출
    for now in graph[start]:
        dfs_recursive(graph, now)


graph = {
    'A': ['B'],
    'B': ['A', 'H', 'C'],
    'C': ['B', 'D'],
    'D': ['C', 'E', 'G'],
    'E': ['D', 'F'],
    'F': ['E'],
    'G': ['D'],
    'H': ['B', 'I', 'J', 'M'],
    'I': ['H'],
    'J': ['H', 'K'],
    'K': ['J', 'L'],
    'L': ['K'],
    'M': ['H']
}

print(dfs_stack(graph, 'A'))  
print(dfs_recursive(graph, 'A'))

DFS를 활용한 문제 해결

앞서 BFS로 풀었던 문제를 이번에는 DFS로 해결해보았다.
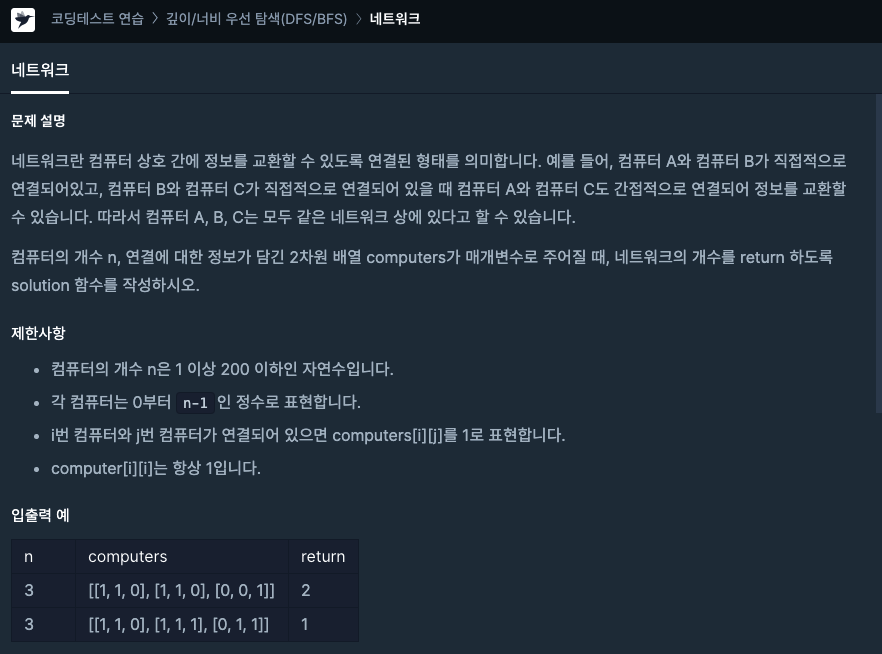
코딩테스트 연습 > 깊이/너비 우선 탐색(DFS/BFS) > 네트워크

# 네트워크(DFS)
def dfs(k, graph, visited):
    visited[k] = True  # 방문 표시
    for i in range(len(graph[k])):
        # 아직 방문하지 않은 인접 정점들에 대해 재귀 수행
        if not visited[i] and graph[k][i] == 1:
            dfs(i, graph, visited)


def solution(n, computers):
    ans = 0
    visited = [False] * n  # 방문 여부를 표시할 리스트
    for i in range(n):
        if not visited[i]:
            # 아직 방문하지 않은 경우, 해당 정점에 대해 재귀 수행
            dfs(i, computers, visited)
            ans += 1    
        if all(visited):
            break
    return ans