Leetcode #3 Longest Substring Without Repeating Characters

문제

String 형인 str 인자에서 중복되지 않은 알파벳으로 이루어진 제일 긴 단어의 길이를 반환해주세요.

str: 텍스트
return: 중복되지 않은 알파벳 길이 (숫자 반환)

예를 들어,

str = "abcabcabc"
return 은 3
=> 'abc' 가 제일 길기 때문

str = "aaaaa"
return 은 1
=> 'a' 가 제일 길기 때문

str = "sttrg"
return 은 3
=> 'trg' 가 제일 길기 때문

나의 풀이

def get_len_of_str(s):
    # 아래 코드를 작성해주세요.
    result = []

    for a in range(0, len(s) + 1):
        for b in range(0, len(s) + 1):
            if len(list(s[a:b])) == len(set(s[a:b])):
                result.append(s[a:b])

    return max([len(x) for x in result])

• 빈리스트 result생성
• for문 2번으로 문자열에서 생성될 수 있는 모든 값 슬라이싱
• if문으로 슬라이싱 값이 중복된거 없을때만 저장(set로 만들면 중복값이 사라지므로 길이가 달라짐)
• return max([len(i) for i in result])
• ex) len(s) == 3 -> [0:1][0:2] [0:3][1:2] ...

더 나은 해결 방법이 떠오르지 않아 어쩔수 없이 시간복잡도가 $O(n^2)$인 로직밖에 생각하지 못했다.
for문을 한번만 쓰고 값을 비교한다음 큰 값을 비교한다는 생각도 해보았으나 코드를 어떻게 짤지 감이 오지 않았다.

결국 검색을 해보니 슬라이딩 윈도우라는 알고리즘을 알게 되었다.

슬라이딩 윈도우(Sliding Window)

[알고리즘] 슬라이딩 윈도우 알고리즘
길이가 n인 어떤 배열 X가 존재할때, 길이가 n 이하면서 X의 요소를 포함하는 서브 배열의 합계 값을 비교하고자 한다.
이 때 X의 서브 배열을 for 루프로 모든 배열 요소를 특정 길이만큼 순회하면서 합계를 비교하는 것은 비효율적이다.(위 나의 풀이랑 동일하다.)
for 루프를 순회하는 기존 방식에서 서브 배열의 요소를 순회하다 보면 중복되는 요소들이 존재한다.

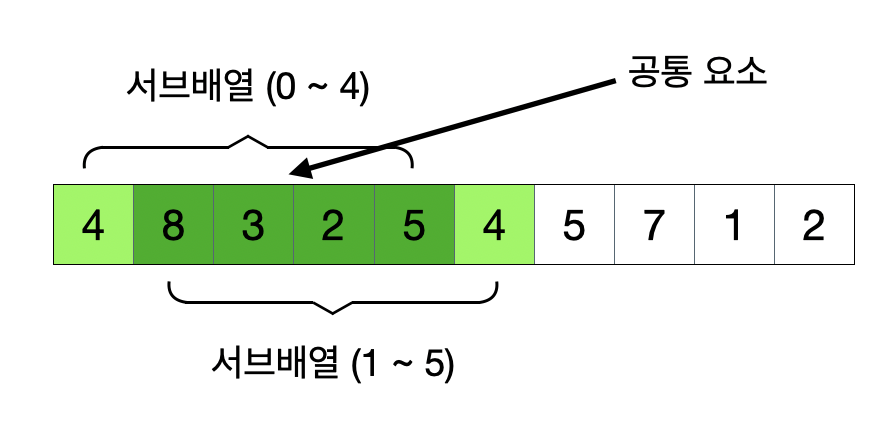
이미지처럼 범위가 5인 서브 배열을 탐색하는 경우 두 서브 배열은 1~4 범위가 중복된다.
이를 재사용하는 알고리즘이 슬라이딩 윈도우다. 코드를 통해 살펴보자.

def max_sub_array(arr, k):
    window_sum = 0
    max_sum = 0
    window_start = 0

    for window_end in range(len(arr)):
        window_sum += arr[window_end]  # 슬라이딩 인덱스 범위 요소 합산
        
        # 슬라이딩 윈도우의 범위가 k 보다 커진 경우
        if window_end >= (k - 1):
            max_sum = max(max_sum, window_sum)
            window_sum -= arr[window_start]  # 슬라이드 윈도우 범위를 벗어난 요소를 합계에서 제거
            window_start += 1  # 슬라이드 윈도우 시작 인덱스 증가

    return max_sum


if __name__ == '__main__':
    print(max_sub_array([2, 4, 7, 10, 8, 4], 3))

# 결과: 25 (7 + 10 + 8)

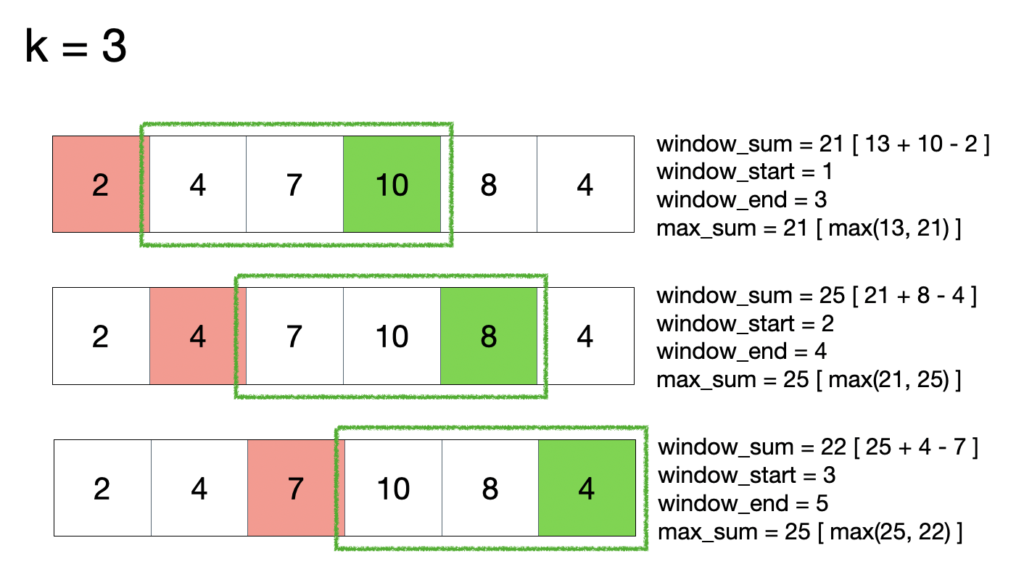
• 길이가 3인 서브 배열을 순회하면서 값을 비교한다고 했을 때, 인덱스의 시작과 마지막 값의 변수를 선언한다.(window_start, window_end)
• 순회를 할 때마다 이전 값과 이전 값에서 다음 순회값의 인덱스의 시작을 더하고 마지막을 뺀 값을 max()함수를 통해 window_end가 기존 배열의 길이에 도달할 때 까지 비교한다.
• 이전 값을 재사용하므로 for 루프를 한번만 사용하게 된다.

위 포스팅을 통해서 슬라이딩 윈도우가 어떤 방식으로 진행되는지 알게 되었다. 배운 내용을 적용해 중복되지 않은 알파벳의 최대 길이를 반환하는 문제의 코드를 짜보았다.

def get_len_of_str(s):
    # dct	= 파라미터로 받은 문자열을 해싱할 빈 딕셔너리 선언
    # end	= 슬라이딩 윈도우의 끝 인덱스값(right)
    # start	= 슬라이딩 윈도우의 시작 인덱스값(left)
    # maxvalue	= 현재 슬라이딩 윈도우의 최댓값
    
	dct = {}
	maxvalue = end = start = 0
    
	for index, i in enumerate(s):	# [{s[0] : 0} , {s[1]: 1} ...{i,index}]
		if i in dct and dct[i] >= start: 	# 중복 문자열을 찾음
			maxvalue = max(maxvalue, end)	# 중복 문자열 '길이'의 최댓값
  			end = index - dct[i]		# 중복 문자열 길이의 최댓값 저장(중복 문자열의 인덱스 - 현재 문자열의 인덱스)
			start = dct[i] + 1 		# 시작점 인덱스 값 1 증가
		else:
			end += 1	# 중복 문자열이 없다면 윈도우의 끝 인덱스값 1 증가
		dct[i] = index 		# 문자열을 탐색할 때마다 dct에 위치 저장(start와 비교하기 위해서)
	return max(mavalue, end)

• Window의 end가 가리키는 값이 현재 윈도우에 존재하는지 체크(중복검사)
• Window에 end가 가리키는 값이 없다면, Window에 해당 string 추가
• Window에 end가 가리키는 값이 있다면, Window에 처음 값 제거