그래프 최단 경로와 플로이드(Floyd-Warshall) 알고리즘

dropKick·2020년 6월 22일

알고리즘 자료구조 자바

자료구조와 알고리즘

목록 보기

14/17

목표

플로이드 워셜 알고리즘을 이해한다.

플로이드 워셜 알고리즘

가중치 방향 그래프 기반, 무방향도 가능
All to All, 모든 정점에 대한 최단 경로
모든 정점은 1 ~ n까지의 정수 인덱스 소유
음의 가중치 가능
Dynamic Programming 기법을 사용
근데 다이나믹 프로그래밍은 다이나믹하지도 프로그래밍도 아니다
문제를 쪼개고 풀고 그걸 다시 문제를 푸는데 이용하는데 오히려 분할 정복에 가깝다

플로이드 알고리즘의 로직

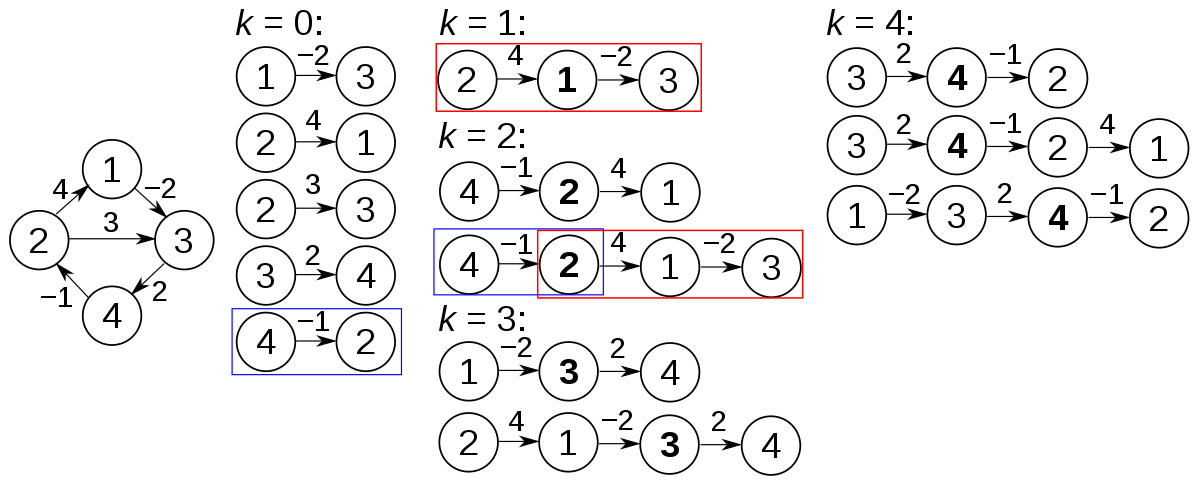
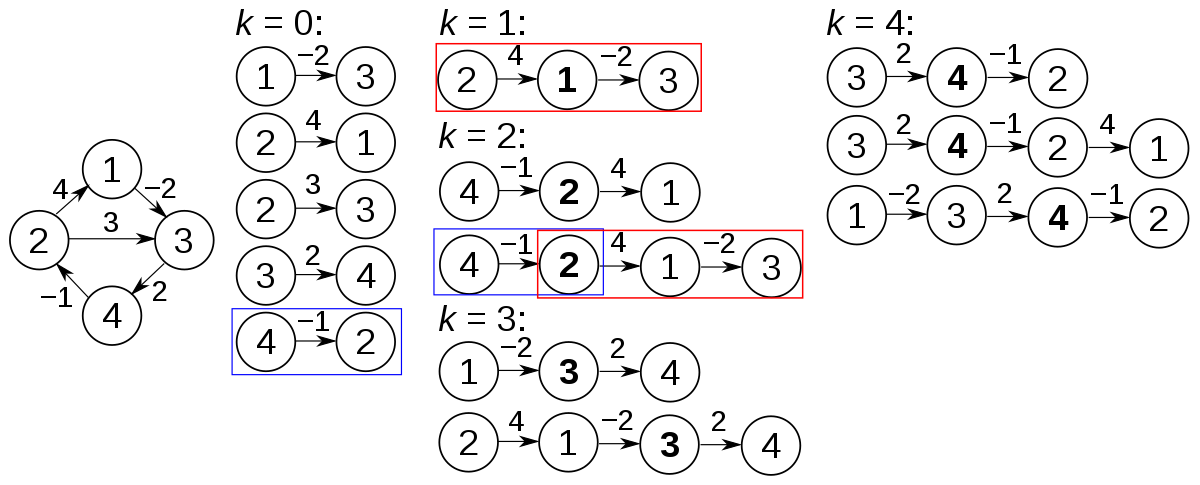
이런 그래프가 있다고 했을 때 최단 경로를 한다면 이렇게 구하자는거다
1. 모든 경로에 대한 가중치를 입력한다.
2. 이렇게 나온 가중치는 최단 경로가 아니다.
정점 3으로 가는건 2->3 보다 2->1->3이 최단경로가 된다.
3. 이제 각 정점에 대해 최단 경로를 갱신한다.
4. 갱신된 경로를 이용해 다시 경로를 갱신한다.
5. 결국 K번째 연산이 수행됐을 때 우리가 원하는 모든 정점을 거치는 최단 경로가 완성된다.

시간복잡도와 연산

단순하게 반복을 3번 써서 비교하고 대입 연산한다
K번까지 $O(n)$ , 2차원 배열 $O(n^2)$ = $O(n^3)$

플로이드 알고리즘이 어떻게 최단 경로를 구성하는가?

요컨대 우리가 알고싶은건 $k$ 까지의 연산과 $k-1[i,k]$ , $k-1[k,j]$ 를 지키지 않고 그냥 대입하는데 어떻게 최단 경로가 구성되는가인데 굉장히 간단하다.

$j$ 는 항상 $k$ 보다 크기때문에 $k$ 를 늘려가면 모든 거쳐가는 정점을 알 수 있고
그 정점에서 최소의 가중치만 가진 경로를 추출해내면 된다.
$k-1$ 인 정점의 경우 원래 경로의 구성은 마지막 정점 $j$ 의 바로 앞노드까지 이루어진다.
그렇기때문에 $k-1[i,k]$ , $k-1[k,j]$ 과 $(i,k)(k,j)$ 는 같다.

경로 추적

우리가 알고싶은 건 거리가 아닌 경로인데 이 경로를 어떻게 추적할까
기록용 배열을 따로 두고 최단 거리로부터 각 경로를 따라 이동하면 되는데
이는 $i$ 와 $j$ 가 있다면 그 사이의 모든 정점을 거치기만 한다면 경로를 추적할 수 있기때문이다.
알면서도 설명이 좀 어려운데 간단하게 설명되어 있는 링크가 있다.
바킹독 경로복원

자바 플로이드 알고리즘의 구현

public void floyd() {
        long[][] spfArr = new long[graph.length][graph.length];
        for (int i = 0; i < graph.length; i++) { // 수행 할 배열
            System.arraycopy(graph[i], 0, spfArr[i], 0, spfArr.length);
        }
        for (int i = 0; i < spfArr.length; i++) { // 자기 자신으로 가는 길은 거리 0
            spfArr[i][i] = 0;
        }
        for (int k = 0; k < spfArr.length; k++) { // 거치는 정점 K
            for (int i = 0; i < spfArr.length; i++) { // 정점 K에 대해 모든 정점 순회
                for (int j = 0; j < spfArr.length; j++) {
                    // 기존 거리와 정점을 거치는 거리 비교
                    spfArr[i][j] = Math.min(spfArr[i][j], (spfArr[i][k] + spfArr[k][j]));
                }
            }
            for (long[] i : spfArr) {
                System.out.println(Arrays.toString(i));
            }
            System.out.println();
        }
    }

출력
[0, 4, 1, 1, 2147483647]
[4, 0, 5, 5, 8]
[1, 5, 0, 2, 15]
[1, 5, 2, 0, 6]
[2147483647, 8, 15, 6, 0]

[0, 4, 1, 1, 12]
[4, 0, 5, 5, 8]
[1, 5, 0, 2, 13]
[1, 5, 2, 0, 6]
[12, 8, 13, 6, 0]

[0, 4, 1, 1, 12]
[4, 0, 5, 5, 8]
[1, 5, 0, 2, 13]
[1, 5, 2, 0, 6]
[12, 8, 13, 6, 0]

[0, 4, 1, 1, 7]
[4, 0, 5, 5, 8]
[1, 5, 0, 2, 8]
[1, 5, 2, 0, 6]
[7, 8, 8, 6, 0]

[0, 4, 1, 1, 7]
[4, 0, 5, 5, 8]
[1, 5, 0, 2, 8]
[1, 5, 2, 0, 6]
[7, 8, 8, 6, 0]