문제
BOJ18769_그리드 네트워크
(이 문제는 Node.js 로 풀면 9점짜리 서브테스크에서 메모리 초과가 발생합니다.)
코드
const filePath = process.platform === 'linux' ? '/dev/stdin' : './Javascript/input.txt';
const input = require('fs').readFileSync(filePath).toString().trim().split('\n');
const T = +input[0];
let inputIdx = 1;
for (let i = 0; i < T; i++) {
const [r, c] = input[inputIdx++].split(' ').map(Number);
const edges = [];
// 수평(행) 간선 연결
for (let i = 0; i < r; i++) {
const row = input[inputIdx++].split(' ').map(Number);
for (let j = 0; j < c - 1; j++) {
edges.push([row[j], i * c + j, i * c + j + 1]); // [cost, a, b]
}
}
// 수직(열) 간선 연결
for (let i = 0; i < r - 1; i++) {
const col = input[inputIdx++].split(' ').map(Number);
for (let j = 0; j < c; j++) {
edges.push([col[j], i * c + j, (i + 1) * c + j]); // [cost, a, b]
}
}
// 크루스칼 알고리즘 수행
edges.sort((a, b) => a[0] - b[0]);
const parents = Array(r * c).fill(0);
for (let i = 0; i < r * c; i++) {
parents[i] = i;
}
let answer = 0;
for (let [cost, a, b] of edges) {
// 사이클을 생성하지 않는다면
if (find(parents, a) !== find(parents, b)) {
union(parents, a, b);
answer += cost;
}
}
console.log(answer);
}
// 루트 노드 찾기
function find(parents, x) {
if (parents[x] !== x) parents[x] = find(parents, parents[x]);
return parents[x];
}
function union(parents, a, b) {
a = find(parents, a);
b = find(parents, b);
if (a < b) parents[b] = a;
else parents[a] = b;
}풀이
이 문제는 클루스칼 알고리즘을 구현할 줄 안다면 쉽게 풀 수 있는 문제였다.
오히려 알고리즘 구현보다 입력으로 들어오는 간선 정보를 저장해주는 과정이 더 복잡했다.
입력값 받기
입력값을 받을 때 shift() 나 splice() 를 사용하지 않고 인덱스(inputIdx)를 사용한 이유는 코드 수행 시간을 개선하기 위해서다.
shift():splice():Array[index]:
예제 입력이 아래와 같이 주어졌다고 가정해보자
1 <- T
2 3 <- r,c
1 3 <- row
3 1 <- row
2 4 2 <- col위 입력값으로 간선의 정보를 아래와 같이 저장해줄 수 있다.
const edges = [];
// 수평(행) 간선 연결
for (let i = 0; i < r; i++) {
const row = input[inputIdx++].split(' ').map(Number);
for (let j = 0; j < c - 1; j++) {
edges.push([row[j], i * c + j, i * c + j + 1]); // [cost, a, b]
}
}위 코드를 수행하면 아래와 같은 형태로 간선과 노드가 이어진다.
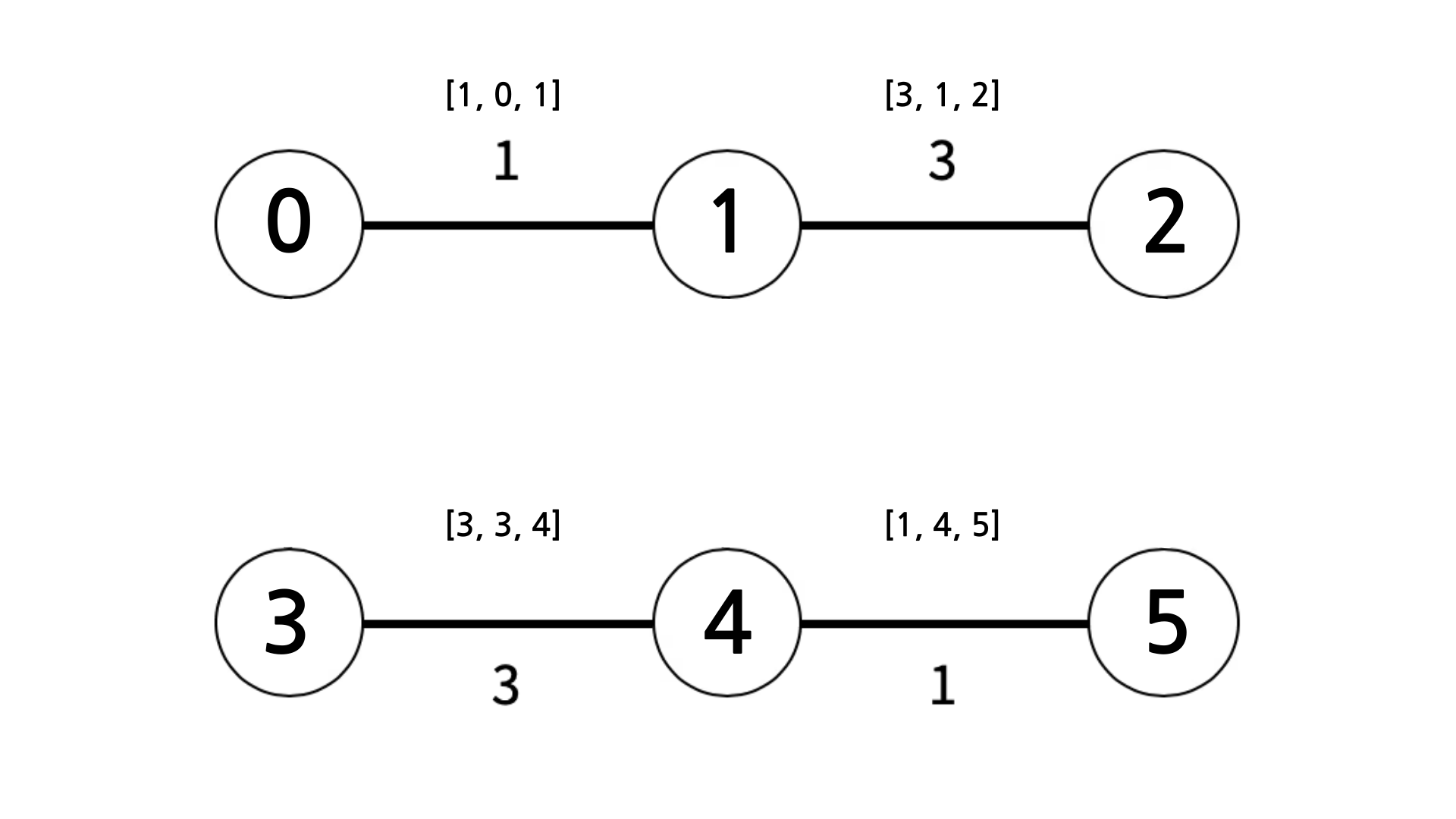
그리고 여기에 아래 코드를 추가한다.
// 수직(열) 간선 연결
for (let i = 0; i < r - 1; i++) {
const col = input[inputIdx++].split(' ').map(Number);
for (let j = 0; j < c; j++) {
edges.push([col[j], i * c + j, (i + 1) * c + j]); // [cost, a, b]
}
}그러면 아래와 같은 그래프가 완성된다.
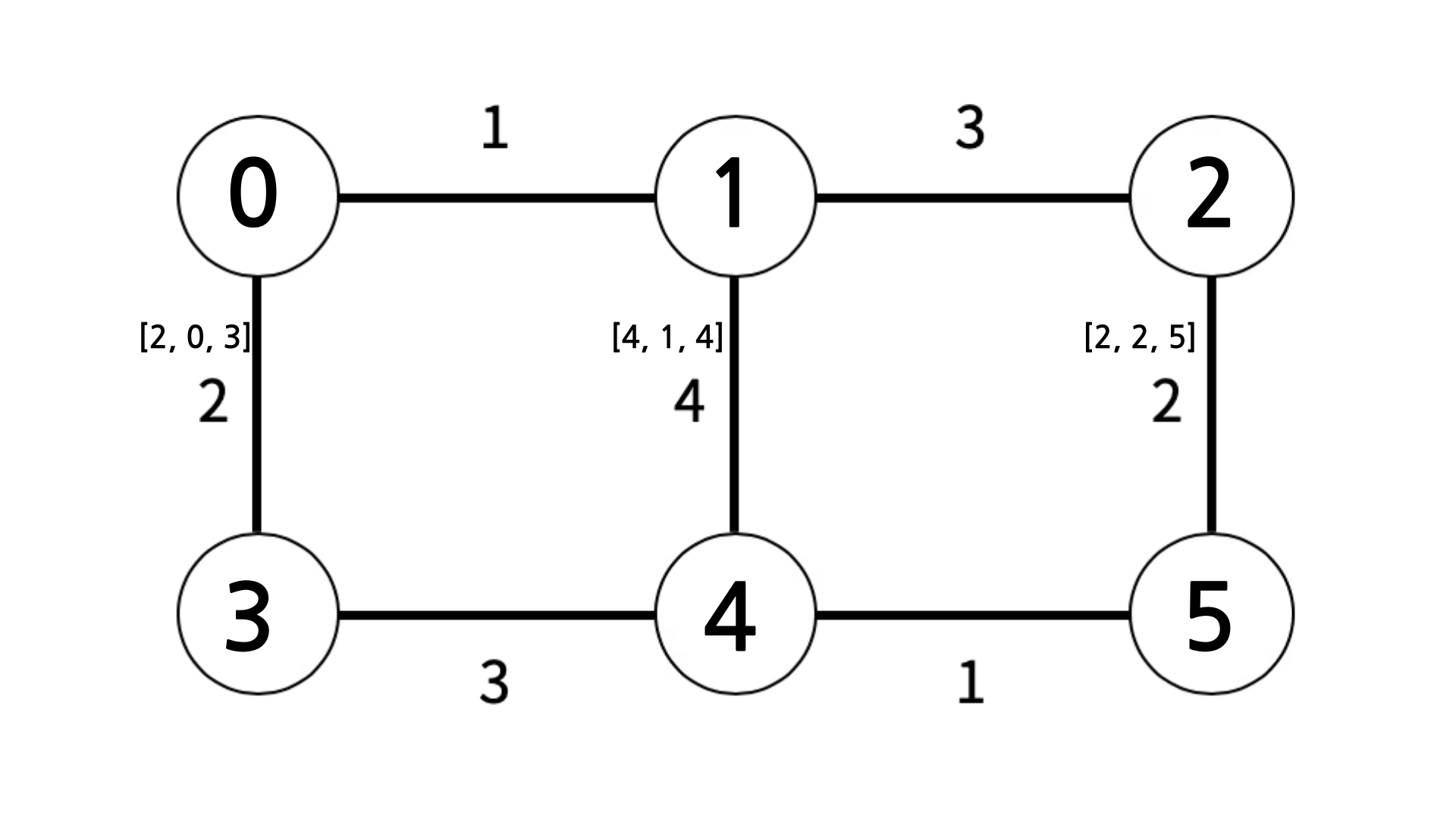
그리고 크루스칼 알고리즘으로 최소 신장 트리를 만들어서 간선의 총 비용을 출력해주면 된다.



