[백준] 4386 별자리 만들기 (Javascript)

문제

BOJ4386_별자리 만들기

풀이

모든 별들은 직/간접 적으로 이어져 있어야 하고, 최소 비용을 들여 모든 별을 이어야 하는 즉, 최소 신장 트리를 만들어야 하는 문제다.

이는 크루스칼 알고리즘(유니온 파인드)를 이용해 만들 수 있다.

다만 별 간의 거리를 알려주지 않으므로 별들 간의 거리를 구해주어여한다.

입력값으로 2차원 좌표에서의 x축 지점과, y축 지점을 알려주기 때문에 아래 공식을 이용해 두 점 사이의 거리를 구할 수 있다.

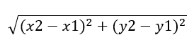
이렇게 모든 별들 간의 거리를 구해서 이를 tree에 저장한 다음 크루스칼 알고리즘을 이용해서 풀면 된다.

출력은 소숫점 둘 째 자리까지 표현해야 하므로 toFixed 메서드를 이용하자.

코드

const filePath = process.platform === 'linux' ? '/dev/stdin' : './Javascript/input.txt';
const input = require('fs').readFileSync(filePath).toString().trim().split('\n');
const n = +input[0];
const arr = input.slice(1).map((e) => e.split(' ').map(Number));
const parent = Array(n);
const tree = [];
let answer = 0;

// 두 점 사이의 거리 구하기
for (let i = 0; i < n; i++) {
    for (let j = i + 1; j < n; j++) {
        const powX = Math.pow(arr[i][0] - arr[j][0], 2);
        const powY = Math.pow(arr[i][1] - arr[j][1], 2);
        const dist = Math.sqrt(powX + powY);
        tree.push([i, j, dist]);
    }
}

// 거리 순으로 정렬
tree.sort((a, b) => a[2] - b[2]);

// 각 노드의 부모 노드 초기화
for (let i = 0; i < n; i++) {
    parent[i] = i;
}

tree.forEach(([a, b, dist]) => {
    if (find(a) !== find(b)) {
        union(a, b);
        answer += dist;
    }
});

console.log(answer.toFixed(2));

function union(a, b) {
    a = find(a);
    b = find(b);
    if (a < b) parent[b] = a;
    else parent[a] = b;
}

function find(x) {
    if (parent[x] !== x) x = find(parent[x]);
    return x;
}