[프로그래머스] 조이스틱 (Javascript)

문제

[프로그래머스] 조이스틱

문제 정의

조이스틱을 움직여서 원하는 문자열을 만들어야 한다.
처음에 문자열은 원하는 문자열의 길이만큼 'A'로 채워져있다.
예를 들어 "JAZ"를 만들어야 한다면 처음에는 "AAA"로 채워져있다.

조이스틱을 위로 움직일 경우 알파벳이 A->B->C-> ... -> Z 순으로 바뀌고, 아래로 움직일 경우 Z->Y->X-> ... -> A 순으로 바뀐다.
만약 'A'에서 아래로 움직이면 'Z'로 바뀌고, 'Z'에서 위로 움직이면 'A'로 바뀐다.

조이스틱을 좌우로 움직일 경우 커서가 왼쪽 오른쪽으로 이동하며 커서가 첫 번째 문자를 가리키고 있을 때 조이스틱을 좌로 움직이면 커서는 마지막 문자로 이동하고, 마지막 문자에서 우로 움직이면 커서는 첫 번째 문자로 이동한다.

또한 문제에서는 명시되어있지 않지만 초기에 커서는 맨 앞 문자를 가리킨다.

해결방안

풀이 1 (74.1점)

function solution(name) {
    let answer = 0;
    let str = 'A'.repeat(name.length);
    const visited = Array(name.length).fill(false);
    let curIdx = 0;

    while (str !== name) {
        let closeDist = Infinity;
        let closeIdx = curIdx;
        // 가장 가까운 인덱스 찾기
        for (let i = 0; i < name.length; i++) {
            if (name[i] !== 'A' && !visited[i]) {
                const dist = getDist(curIdx, i, name.length);
                if (dist < closeDist) {
                    closeDist = dist;
                    closeIdx = i;
                }
            }
        }
        curIdx = closeIdx; // 가장 가까운 인덱스로 커서 이동
        answer += closeDist; // 이동 횟수 누적
        visited[curIdx] = true;

        const from = str[curIdx].codePointAt() - 65;
        const to = name[curIdx].codePointAt() - 65;
        const dist = getDist(from, to, 26); // 두 알파벳 사이의 최단 거리
        answer += dist;
        str = str.slice(0, curIdx) + name[curIdx] + str.slice(curIdx + 1); // 알파벳 변경
    }

    // 거리 구하는 함수
    function getDist(from, to, n) {
        const diff = Math.abs(from - to);
        return Math.min(diff, n - diff);
    }

    return answer;
}

처음에 시도했던 접근 방법은 이렇다.

현재 인덱스(curIdx) 에서 가장 거리가 가깝고 'A'가 아닌 곳의 인덱스(closeIdx)를 구한다. 또한 이미 방문했던 곳은 다시 방문할 필요가 없기 때문에 visited를 이용해서 방문 여부를 확인해준다.

let closeDist = Infinity;
let closeIdx = curIdx;
// 가장 가까운 인덱스 찾기
for (let i = 0; i < name.length; i++) {
  if (name[i] !== 'A' && !visited[i]) {
    const dist = getDist(curIdx, i, name.length);
    if (dist < closeDist) {
      closeDist = dist;
      closeIdx = i;
    }
  }
}

getDist() 함수는 왼쪽으로 이동했을 때와 오른쪽으로 이동했을 때 중에서 더 빠른 거리를 리턴해준다.

// 거리 구하는 함수
function getDist(from, to, n) {
  const diff = Math.abs(from - to);
  return Math.min(diff, n - diff);
}

예를 들어 문자열 "ABC"가 있고 'A'에서 'C'로 이동한다고 가정해보자.
'A'의 인덱스는 0(from = 0)
'C'의 인덱스는 2(to = 2)
문자열의 길이는 3(n = 3)이 되고,
따라서 diff = 2, Math.min(2, 1) = 1 이 된다. 이는 곧바로 가면 2칸을 이동해야 되고 반대로 가면 1칸만 이동하면 된다는 것을 의미한다.

이렇게해서 가장 가까운 거리를 찾았으면 해당 인덱스로 커서를 이동시키고 이동 횟수를 answer에 누적해준다.

curIdx = closeIdx; // 가장 가까운 인덱스로 커서 이동
answer += closeDist; // 이동 횟수 누적
visited[curIdx] = true;

그리고 커서가 가리키고 있는 위치의 현재 알파벳(str[curIdx])과 만들어야 하는 알파벳(name[curIdx])까지의 최소 이동 횟수를 구한다.
이때도 getDist() 함수를 이용해줄 수 있다.

const from = str[curIdx].codePointAt() - 65;
const to = name[curIdx].codePointAt() - 65;
const dist = getDist(from, to, 26); // 두 알파벳 사이의 최단 거리
answer += dist;
str = str.slice(0, curIdx) + name[curIdx] + str.slice(curIdx + 1); // 알파벳 변경

그리고 그 횟수만큼 answer에 누적한 다음 현재 문자열인 str을 변경한다. 이 과정을 str이 name과 같아질 때까지 반복한다.

반례

"ABABAAAAABA"

correct: 10 
wrong: 11

올바른 이동은 아래와 같이 이동해야 최소 이동횟수를 구할 수 있다.
← ← ↑ → → → ↑ → → ↑

하지만 풀이1의 코드는 아래와 같이 이동한다.
→ ↑ → → ↑ ← ← ← ← ← ↑

따라서 매번 가장 가까운 거리로 커서를 옮기는 방법은 잘못됐다.

풀이 2 (통과)

function solution(name) {
    let answer = 0;
    let min = name.length - 1; // 최소 이동 횟수

    for (let i = 0; i < name.length; i++) {
        const curAlphabet = name[i].codePointAt();
        const dist = getDist(65, curAlphabet, 26);
        answer += dist;

        let nextIdx = i + 1;
        // A가 아닌곳을 찾을 때까지 nextIdx를 1씩 증가
        while (nextIdx < name.length && name[nextIdx] === 'A') nextIdx++;

        min = Math.min(
          min, 
          i * 2 + name.length - nextIdx,
          i + (name.length - nextIdx) * 2
        );
    }
    answer += min;

    // 거리 구하는 함수
    function getDist(from, to, len) {
        const diff = Math.abs(from - to);
        return Math.min(diff, len - diff);
    }

    return answer;
}

우선 이동 횟수는 최대 name.length-1 번이다. 한 문자를 방문했을 때, 그 문자를 원하는 문자로 바꿀 수 있어서 다시 방문할 필요가 없기 때문이다. 1을 빼주는 이유는 커서가 처음에 위치해 있는 곳은 이동 횟수로 치지 않기 때문이다.
따라서 min = name.length-1로 초기화 해준다.

그리고 커서는 움직이지 않고, 우선 알파벳을 바꾸는 횟수만 구해준다고 생각하자. (커서는 아직 첫 번째 알파벳을 가리키고 있다고 생각하자)

const curAlphabet = name[i].codePointAt();
const dist = getDist(65, curAlphabet, 26);
answer += dist;
...

function getDist(from, to, len) {
  const diff = Math.abs(from - to);
  return Math.min(diff, len - diff);
}

curAlphabet은 현재 인덱스의 알파벳의 아스키코드에 대한 정보를 담는다. name[i] === 'A'일 경우 curAlphabet = 65가 된다.

그리고 getDist() 함수를 사용해서 현재 알파벳과 초기 알파벳인 'A' 사이의 최소 이동 횟수를 구해주자. (getDist() 함수는 풀이 1에서 사용한 것과 동일하다.)

그리고 nextIdx 라는 변수를 만들어서 'A'가 아닌 알파벳을 만날때까지 계속해서 1씩 증가시킨다.

let nextIdx = i + 1;
// A가 아닌곳을 찾을 때까지 nextIdx 증가
while (nextIdx < name.length && name[nextIdx] === 'A') nextIdx++;

while문이 종료되면 nextIdx는 A가 아닌 문자의 인덱스를 가리킨다.
만약 주어진 문자열이 ABABAAAAABA 이고, 현재 i=0이라면, nextIdx는 1에서 멈춘다.

name = ABABAAAAABA
i = 0
nextIdx = 1

그리고 커서의 초기 위치로부터 i와 nextIdx로 가는 가장 빠른 거리를 찾는다. 현재 커서의 위치는 0(첫 번재 문자)이다.
현재 커서의 위치에서 에서 i와 nextIdx에 방문하는 방법은 세 가지가 있다.

1. 0 에서 name.length-1까지 가는 도중에 i와 nextIdx에 방문하는 방법.
   0 -> i -> nextIdx -> name.length-1

2. 0부터 i까지 갔다가 다시 뒤로 돌아 거꾸로 가서 nextIdx에 방문하는 방법
   0 -> i -> 0 -> name.length-1 -> nextIdx

3. 0에서 처음부터 거꾸로가서 nextIdx에 방문하고 다시 뒤로 돌아와서 i로 가는 방법
   0 -> name.length-1 -> nextIdx -> name.length-1 -> 0 -> i

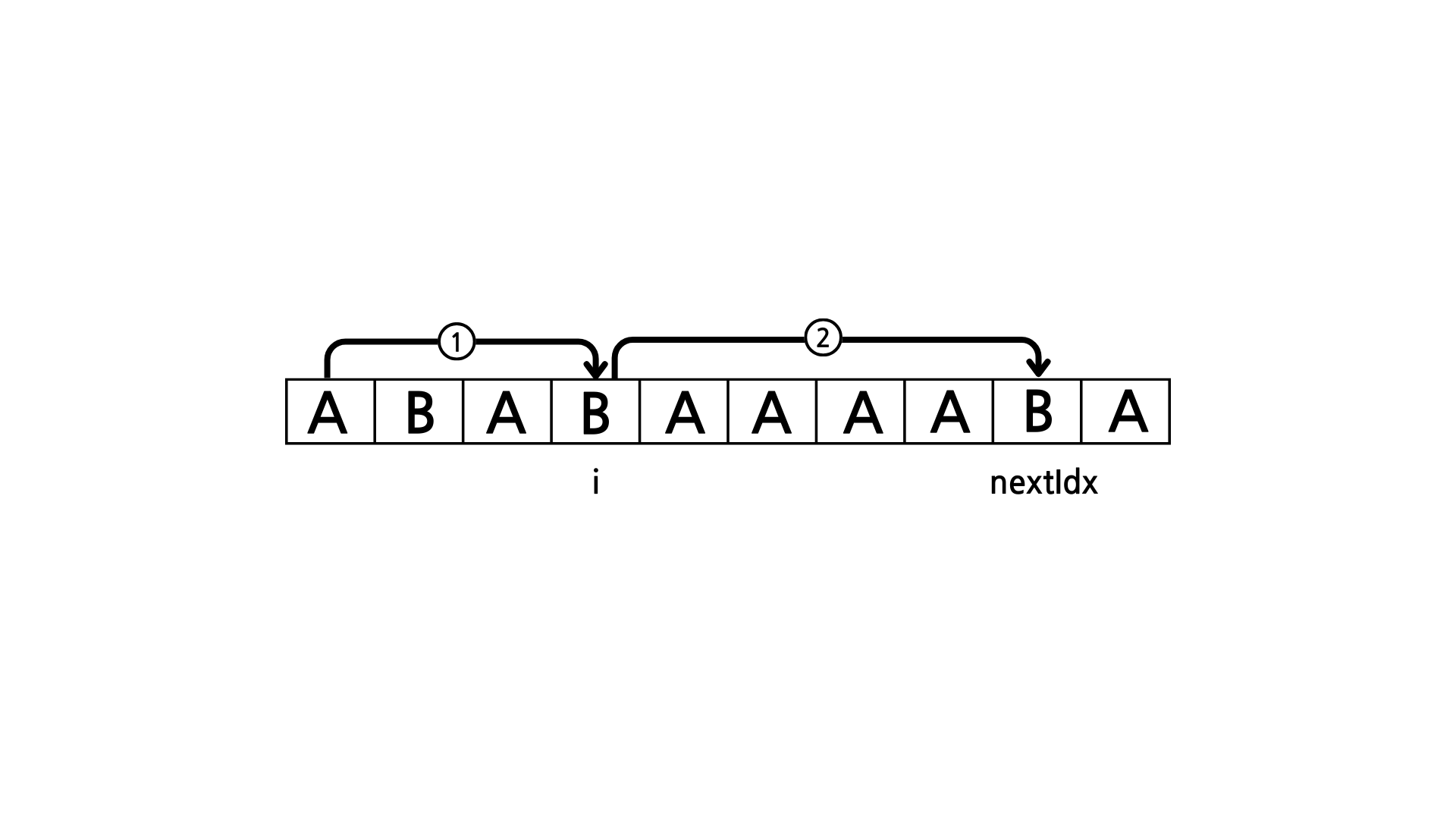
글로만 설명하면 이해가 어려우니 아래 예시를 보자.

name = ABABAAAAABA
i = 3
nextIdx = 9

현재 상태는 위와 같다고 가정했을 때 1,2,3 번은 아래와 같은 순서로 방문한다.

1번
8칸 이동

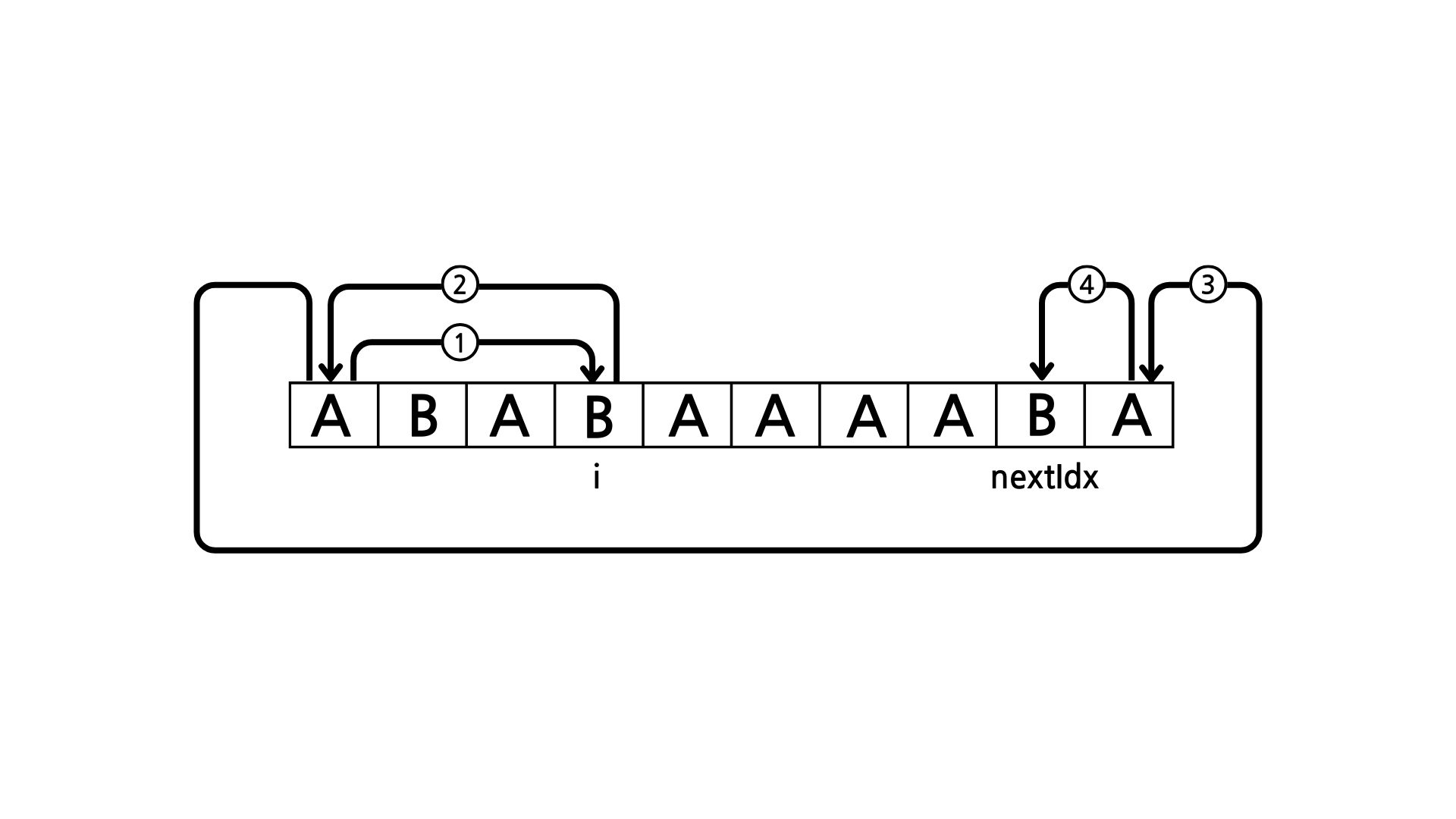
2번
8칸 이동

3번
7칸 이동

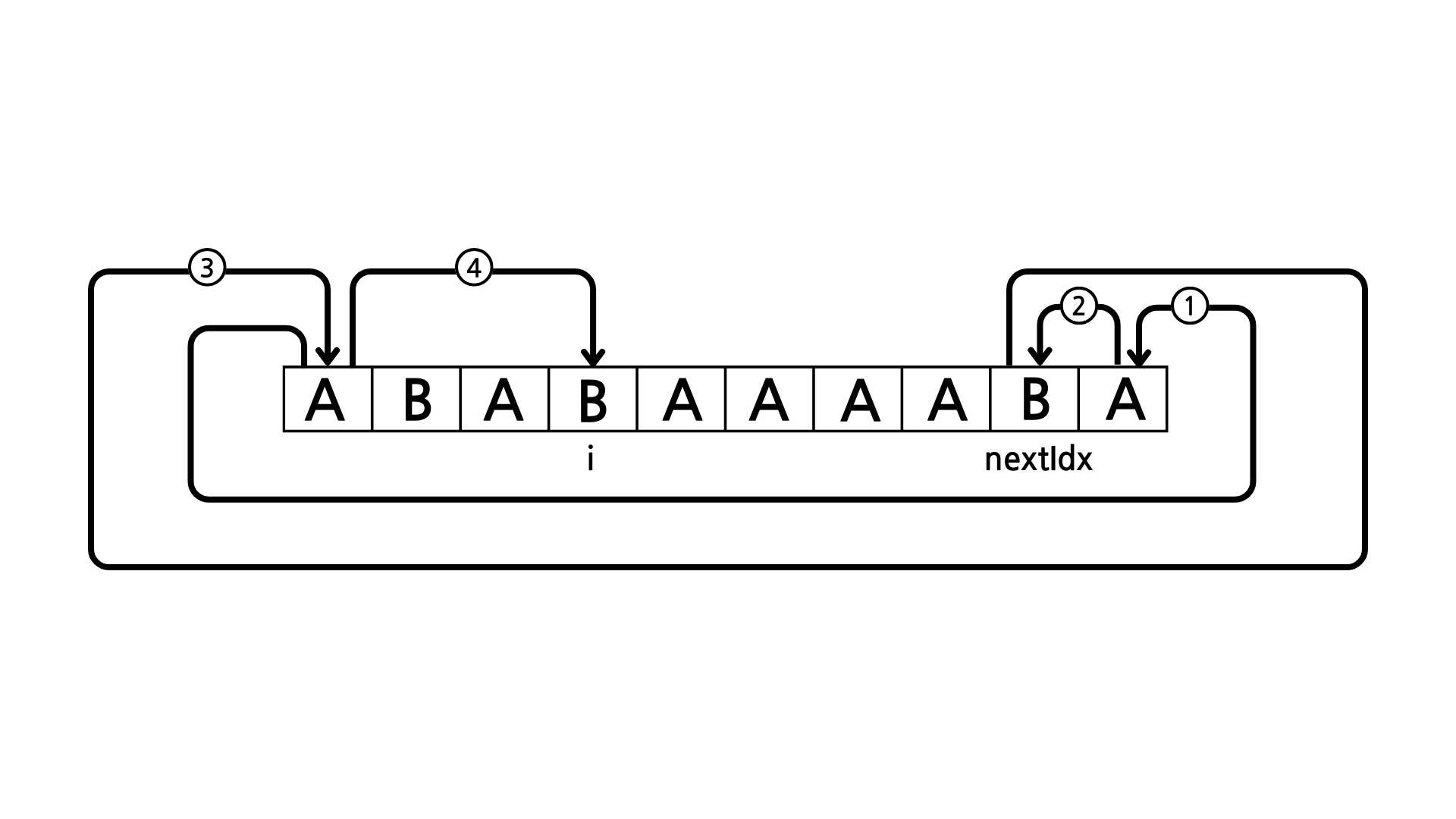
이 경우에는 3번 방법으로 가는 것이 7칸 이동으로 가장 빠른 방법이다.

각각의 방법을 구하는 식은 아래와 같다.

1번
name.length
0번부터 name.length까지 고정적으로 이동함

2번
i*2 + (name.length - nextIdx)
0부터 i까지 갔다가 i에서 0으로 다시 돌아옴 = i*2

• 0부터 nextIdx까지 거꾸로 이동함 = name.length - nextIdx

3번
i + (name.length - nextIdx) * 2
0에서 nextIdx까지 거꾸로 갔다가 다시 0으로 돌아옴 = (name.length - nextIdx) * 2

• 0부터 i까지 감 = i

이를 코드로 작성해보면 아래와 같다.

min = Math.min(
  min, // 기존 최소 거리 (초기에는 name.length)
  i * 2 + name.length - nextIdx, 
  i + (name.length - nextIdx) * 2 
); 

이렇게 하면 반복문이 종료되었을 때 최소 좌우 이동거리를 구할 수 있고, 이를 answer에 누적해주면 된다.