[BOJ 1167] 트리의 지름

트리의 지름
예제의 트리를 그리면 다음과 같다.

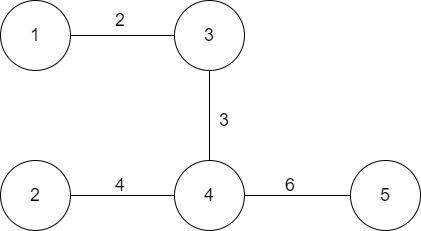
트리의 지름의 정의는 두 정점 사이의 거리 중 가장 긴 것이므로 1-3-4-5를 잇는 거리가 11로 가장 길다. 1에서 DFS/BFS를 하면 가장 큰 거리를 구할 수 있다.
그런데 어느 정점에서 탐색을 해야 최대 거리가 될 것인가? 모든 정점($V$)에 대해 DFS/BFS($O(V+E)$)를 하면 시간복잡도가 $O(V\times (V+E))$가 된다. 너무 비효율적이다.

트리의 지름의 양 끝점에서 DFS/BFS를 하면 가장 먼 거리라는 것을 이용하면 어떨까?
1. 임의의 점 $v_0$에서 가장 먼 정점 $v_1$을 찾는다. (이때, $v_1$은 트리의 지름의 양 끝 점중 하나이다.)
2. $v_1$에서 가장 먼 정점 $v_2$를 찾는다. (이때, $v_2$는 트리의 지름의 양 끝점중 하나이다.)
3. $v_1 \neq v_2$이고, $v_1$과 $v_2$가 트리의 지름의 양끝이므로 사이의 거리가 트리의 지름이 된다.

1과 2에서 DFS/BFS를 호출하므로 총 2번의 DFS/BFS가 전체 시간복잡도를 차지한다. 따라서 여전히 $O(V+E)$이다.
(정확한 증명은 아래 2개의 사이트를 참고)
https://www.quora.com/How-does-following-algorithm-for-finding-longest-path-in-tree-work
https://blog.myungwoo.kr/112

import sys

N = int(input())

# Construct Graph
G = dict()
for i in range(N):
    L = list(map(int, sys.stdin.readline().split()))
    L.pop() # remove -1
    src = L[0]
    G[src] = []
    for j in range(1, len(L), 2):
        dst = L[j]
        cost = L[j + 1]
        G[src].append([cost, dst])


def get_max_vertex(start):
    """ Using BFS """
    q = [[0, start]] # [cost, vertex]
    max_dist = 0
    max_vertex = start
    visit = set()
    visit.add(start)
    while q:
        dist = q[0][0]
        x = q[0][1]
        del q[0] # queue.pop

        # update max_dist, max_vertex
        if max_dist < dist:
           max_dist = dist
           max_vertex = x
        
        for L in G[x]:
            cost = L[0] # weight of the edge
            next = L[1] # destination fo x
            if next not in visit:
                q.append([dist + cost, next])
                visit.add(next)

    return max_vertex, max_dist

# 1번 정점은 항상 존재하므로 임의의 정점으로 삼는다.
v1, dist = get_max_vertex(1)  # v1는 1에서 가장 먼 정점
v2, dist = get_max_vertex(v1) # v2는 v1에서 가장 먼 정점
print(dist)

파이썬에서 시간초과를 벗어나기 위한 방법이다.
나는 2번 이유때문에 처음에 시간초과를 받았다.

1. input()대신에 sys.stdin.readline()을 이용한다.
2. 정점 방문 여부(visit)를 $O(1)$로 할것.
3. queue를 collections의 deque로 한다. (BFS에서)