컴퓨터로 방정식의 해는 어떻게 구하는지 알아보자.
2차방정식이라면 근의 공식을 통해 해결할 수 있지만, 3차 그 이상이라면?
$\sin{x}, \cos{x}, \tan{x}$와 같은 삼각함수가 있다면?
$e^x, \ln{x}$와 같은 지수, 로그함수가 있다면?
$f(x, y, z) = 0$과 같이 미지수가 2개 이상이라면?
이런 방정식의 근의 공식은 존재하지 않는다.
우선 식을 모두 이항하여 $f(x) = 0$로 만들고, 이 방정식의 의 해를 $\alpha$라 하자. ($f(\alpha)=0)$

크게 3가지 방법이 존재한다.

1. Newton's method (뉴턴방법)

고등학교 미적분을 공부할때 접선의 방정식을 이용하여 $\sqrt2$의 근삿값을 구하는 방법이 소개되어있다. (실제로 교육과정에 중요한 내용은 아니다.) 그리고 대학교 미적분학에도 배웠던것 같다.
$y=x^2$의 임의의 점 $x_0$에서 그은 접선의 $x$절편을 $x_1$, 그리고 $x_1$에서 그은 접선의 $x$절편을 $x_2$, ... 이렇게 나가면 $x$절편이 방정식의 근에 가까워지는 것을 이용한 방법이다.
아래 그림을 보면 어떻게 근에 가까워지는지 보여준다.

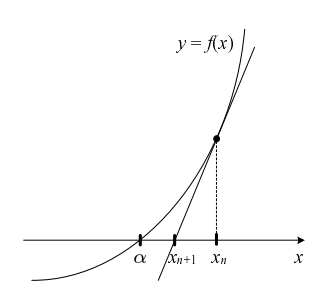
접선의 방정식은
$y = f'(x_n)(x-x_n) + f(x_n)$
이고 이 직선의 $x$ 절편을 $x_{n+1}$이라 하면
$x_{n+1}$ = $x_n-{f(x_n)\over f'(x_n)}$

따라서 다음과 같이 반복문을 구성할 수 있다.
$x_0$: initial guess
for n = 0, 1, 2, 3,...
$x_{n+1}$ = $x_n-{f(x_n)\over f'(x_n)}$

그러나 반복문을 무한히 할 수는 없으므로 적절한 순간에 중단해야한다.

1. 현재 구한 $x_n$에 대해 함수 값이 충분히 작은가?
   1.1 $|f(x_n)| < \delta$
2. 충분히 많은 회수만큼 반복문을 수행하였는가?
   2.1 $n > N_{max}$
3. 현재 구한 $x_{n+1}$이 직전에 구한 $x_n$에 비해 더 이상 의미 있는 진전을 하지 않는가?
   3.1 $|x_{n+1}-x_n| < \epsilon$

이 글에 소개된 3가지 방법 중 가장 빠른 속도로 근에 수렴한다. 그러나 단점이 존재하는데 실제 $f'(x)$를 구하는 비용이 많거나 심지어 함수 $f(x)$ 자체가 근사치로 구한 경우 도함수 자체를 구할 수 없다. 또 $f'(x)=0$이 되는 경우도 근을 구할 수 없다. 이러한 문제점 때문에 또 다른 방법이 필요하다.

2. Secant method (할선법)

접선의 기울기 $f'(x_n)$ 대신에 평균변화율 ${f(x_n) - f(x_{n-1})\over x_n - x_{n-1}}$을 이용한 방법이다.

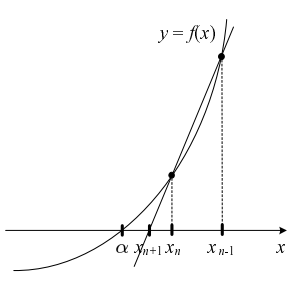
당연히, Newton method보다는 수렴속도가 느리다. 대신에 도함수를 구하지 않고 비교적 저렴한 비용으로, 그리고 도함수를 구하지 못하는 경우에도 방정식의 근의 근삿값을 구할 수 있다.
뉴턴방법과 비슷하게 반복문을 종료한다.

3. Bisection method (이분법)

(위키백과) 반드시 존재하는 폐구간을 이분한 후, 이 중 근이 존재하는 하위 폐구간을 선택하는 것을 반복하여서 근을 찾는 알고리즘이다. (그럴 가능성은 적지만) 알고리즘문제에 나온다면 이분탐색으로 근을 찾으면 된다.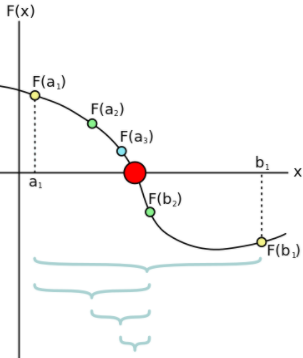
아래 pseudocode를 참고. 이 알고리즘을 수행하려면 반드시 근이 존재하는 구간 $[a, b]$이어야 한다. 구간을 잘 설정하면 수렴속도를 향상시킬 수 있다.

N ← 1
while N ≤ NMAX do // limit iterations to prevent infinite loop
    c ← (a + b)/2 // new midpoint
    if f(c) = 0 or (b – a)/2 < TOL then // solution found
        Output(c)
        Stop
    end if
    N ← N + 1 // increment step counter
    if sign(f(c)) = sign(f(a)) then a ← c else b ← c // new interval
end while

4. 문제

4.1 사다리

[BOJ 2022] 사다리

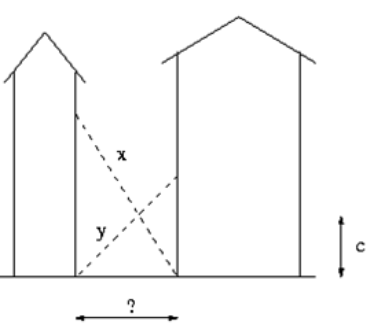
삼각형의 닮음을 이용하여 관계식을 정리하면 식을 구할 수 있다.
(두 직선의 교점을 구해도 된다.)
빌딩이 떨어진 거리를 $a$라 하면
${1}\over{\sqrt{x^2-a^2}}$$+$${1}\over{\sqrt{y^2-a^2}}$$=$${}1\over{c}$
이다. 따라서 방정식을 $f(a)=$${1}\over{\sqrt{x^2-a^2}}$$+$${1}\over{\sqrt{y^2-a^2}}$$-$${}1\over{c}$라 하고 이분법을 이용하면 답을 구할 수 있다.(그러나 예제는 맞는데 '틀렸습니다')
방정식을 작성할 때(특히 실수 연산이 있는 경우) 최대한 오차가 나지 않아야 한다. 위의 식은 분수(실수)가 많아서 오차가 많이 날 가능성이 매우 높다. 따라서 다음과 같이 (수학적으로 동일한) 식을 바꾼다.
$f(a)=$${\sqrt{x^2-a^2}+\sqrt{y^2-a^2}}\over{\sqrt{x^2-a^2}\sqrt{y^2-a^2}}$$-c$
$f(a)=0$을 만족하는 $a$가 근이다.

import math
x, y, c = map(float, input().split())

# f(a) = 0이면 x = a가 근이다
def solve(a):
    global x, y, c
    M = math.sqrt(x*x - a*a)
    N = math.sqrt(y*y - a*a)
    return (M*N)/(M+N) - c

# 반드시 근이 존재하는 구간 설정
x0 = 0
y0 = min(x, y)

val = 0

# 의미있는 진전일 때만 반복
while abs(x0 - y0) > 1e-6:
    # 방정식의 후보 근
    a = (x0 + y0) / 2.0
    val = solve(a)
    
    #print(val), 방정식이 해에 근접하는지 확인
    if val < 0:
        y0 = a
    else:
        x0 = a

# 방정식의 근 출력
print('%.3f' % round(a, 3))

4.2 Ax+Bsin(x)=C (2)

정수 A, B, C가 입력으로 주어졌을 때, 방정식 $Ax+B\sin{(x)}=C$의 근을 구하는 문제이다.
$f(x)=Ax+B\sin{(x)}-C$ 라 하면
$f'(x)=A+B\cos{(x)}$ 이므로 뉴턴법을 이용하여
$f(x)=0$ 의 해를 구할 수 있다.

import sys
#sys.stdin = open('input.txt', 'r')
sys.setrecursionlimit(int(1e5))
input = sys.stdin.readline

import math

def fx(A, B, C, x):
    return A * x + B * math.sin(x) - C

def dfx(A, B, x):
    return A + B * math.cos(x)

A, B, C = map(int, input().split())
epsilon = 1e-9

cur = 0
next = 0
while math.fabs(fx(A, B, C, cur)) > epsilon:
    next = cur - fx(A, B, C, cur) / dfx(A, B, cur)
    cur = next
print(f'{cur:.10f}')