시간 복잡도
개요
시간 복잡도란 알고리즘을 수행할 때 걸리는 시간을 기준으로 효율성을 분석하는 것입니다. 시간의 효율성이란 결국 알고리즘에서 비교와 교환 등이 일어날 때 연산자의 처리 횟수가 적다는 의미이며, 연산자의 처리 횟수가 적다는 건 시간의 복잡도가 낮다는 의미입니다.
Big-O 표기법
Big-O 표기법은 컴퓨터 과학에서 "대략"을 나타내는 공식적인 개념으로 시간 복잡도를 나타내는 표현입니다.
선형 탐색은 비교적 간단한데 찾는 값이 배열의 맨 끝에 있는 최악의 상황의 경우 이 값을 찾는데 n번의 단계를 거치면 됩니다. 이 개념은 O(n)으로 나타냅니다.
버블 정렬에서는 인접해 있는 자료와 쌍을 이루어 비교하기 때문에, n개의 자료를 갖는 배열은 n-1쌍을 비교합니다. n개의 자료가 있을 때 n-1번 비교해주면, n번째의 자료가 정렬되어 있습니다. 그 이후로 n-1개의 자료를 다시 비교하게 됩니다. 전체 비교 횟수는 (n-1) + (n-2) + ... + 1은 n(n-1)/2이며, n^2/2 - n/2로 나타낼 수 있습니다. 시간 복잡도는 가장 중요한(가장 지수가 큰) 부분만 남기고, 계수를 삭제합니다. 따라서 만약 n^2/2 - n/2의 가장 중요한 부분은 n^2/2이 되며 이것은 (1/2)n^2입니다. 계수를 제외하면 n^2이 남고 O(n^2)으로 표현합니다.
선택 정렬은 가장 작은 값(혹은 가장 큰 값)을 찾아 제자리를 찾아줍니다. n개의 자료가 있다면 첫 번째 자료와 나머지 n-1개의 자료 중 가장 작은 값의 자리를 교환해주어야 합니다. n-1개의 자료 중에서 가장 작은 값을 찾기 위해서는 n-1번의 비교가 필요합니다. 즉, 비교 횟순느 버블 정렬과 마찬가지로 (n-1) + (n-2) + ... + 1이며, 시간복잡도는 O(n^2)으로 표현합니다.
삽입 정렬은 n개의 자료가 있다면 첫 번째 자료는 정렬이 되었다고 생각하고, n-1개의 자료 중 첫번째 자료와 정렬된 자료를 비교합니다. 이 때 정렬된 자료는 1개이기 때문에 비교 횟수는 1입니다. 정렬되지 않은 부분에 1개의 자료가 남게 되면, 정렬된 자료의 수 n-1개만큼의 비교가 필요합니다. 따라서 비교 횟수는 1 + 2 + ... + (n-1)이며, 시간복잡도는 O(n^2)으로 표현합니다.
Big Ω 표기법
Big Ω 는 최선의 경우를 나타냅니다.
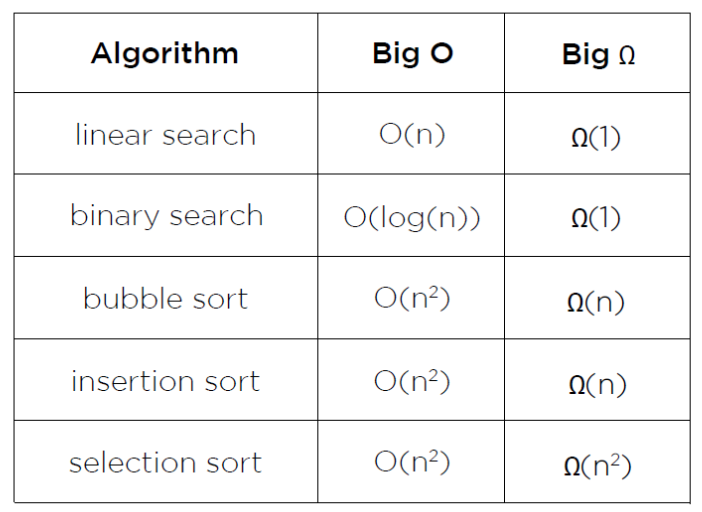
선형 탐색에서 최선의 경우는 배열의 처음에 찾고자 하는 값이 있는 상황입니다. 이는 배열의 크기와 상관없이 Ω(1)이라고 나타냅니다.
버블 정렬에서 최선의 경우 (이미 정렬된 배열)를 생각해보면 버블 정렬은 교환이 이루어지지 않더라도 배열이 정렬된 사실을 모르기 때문에 여전히 n-1번의 비교를 해줘야 합니다. 그래서 최선의 경우는 Ω(n)로 표기합니다.
선택 정렬 역시 배열이 정렬되었다는 것을 알 수 없어서 최소값을 계속 찾아주어야 하므로 Ω(n^2)로 표기합니다.
삽입 정렬은 정렬되지 않은 부분에서 정렬된 부분으로 옮겨갈 때, 정렬된 부분의 가장 큰 수와 비교하기만 하면 되기 때문에 Ω(n)로 표기합니다.

