
문제 링크
문제 분석
고속도로를 지나는 차량의 대수는 1대 이상 10,000대 이하이며 각각의 차량은
-30,000 ~ 30,000의 구간 범위를 가집니다.
효율성 테스트도 함께 이루어지는 문제이기 때문에 시간복잡도, 공간복잡도를
고려하면서 해결해야 하는 문제이며 각 단계에서 최적해를 찾는
그리디 알고리즘을 적용하는 문제입니다.
풀이 코드
import java.util.Arrays;
import java.util.Comparator;
class Solution {
public int solution(int[][] routes) {
int answer = 0;
Arrays.sort(routes, new Comparator<int[]>() {
@Override
public int compare(int[] route1, int[] route2) {
return route1[1] - route2[1];
}
});
int cam = Integer.MIN_VALUE;
for(int[] route : routes) {
if(cam < route[0]) {
// 현재 카메라의 위치가 route의 시작 지점보다 작으면
// 새로운 cam을 route의 종료 지점에 설치한다
cam = route[1];
answer++;
}
}
return answer;
}
}풀이 과정
과정을 설명하기 위해, 문제에 예시로 주어진 [[-20, 15], [-14, -5], [-18, -13], [-5, -3]] 의
풀이 과정을 단계별로 표현하겠습니다. 그림 상태가 좋지 못한 점은 죄송합니다...
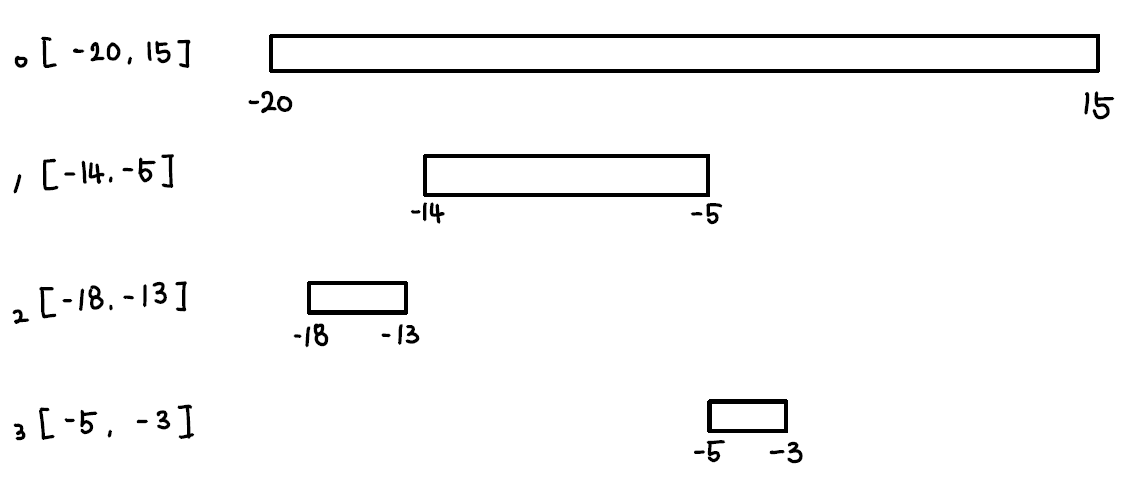
(-13, -14에서 그림에 오류가 있습니다. 죄송합니다 😳)
먼저 주어진 4개의 차량 이동 구간을 그림으로 표현하면 다음과 같습니다.
여기서 구간 종료 위치를 기준으로 오름차순 정렬합니다.
오름차순 정렬을 하는 이유
문제의 핵심은 구간에 카메라를 단 한 번만이라도 만나면 되는 것이기 때문에
종료 위치를 기준으로 오름차순 정렬을 해야 직관적으로 이 차량이 카메라를 무조건
만나야 하는 위치(=종료 위치)에 카메라를 그리디하게 배치할 수 있습니다.
오름차순 정렬
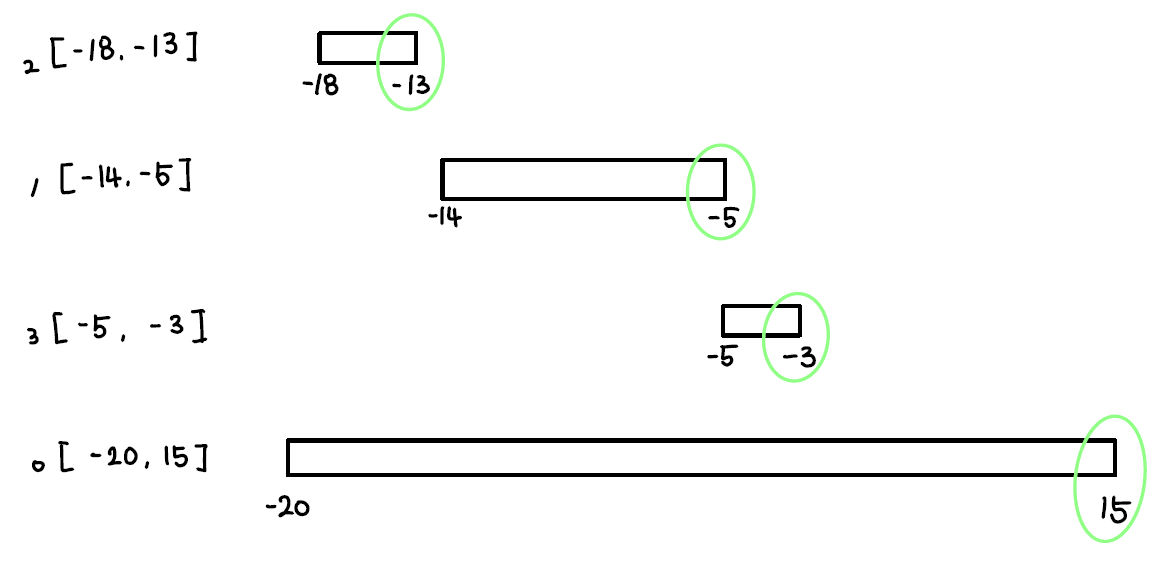
차량 이동을 오름차순 정렬을 하게 된다면 다음과 같은 순서를 가지게 됩니다
이제 우리는 도로의 가장 왼쪽 끝(문제에서는 -20, 코드에서는 MIN_VALUE)
에서부터 카메라 배치를 시작하게 됩니다.
첫 번째 카메라 배치
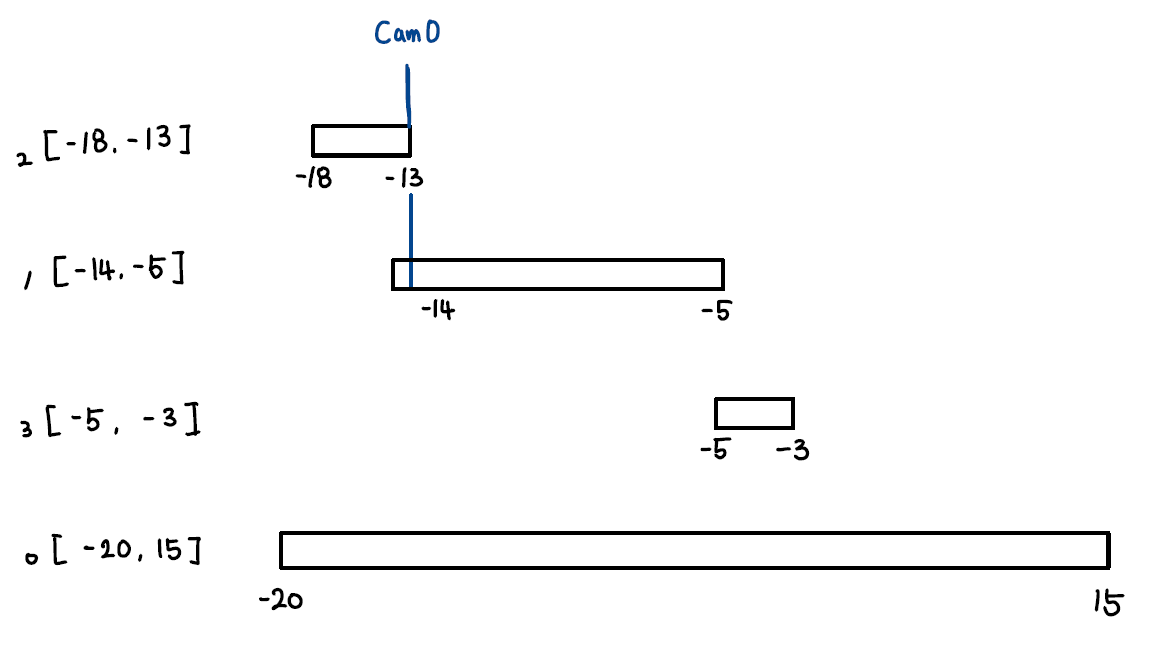
현재 카메라는 아직 설치되지 않았고, 구간 중 가장 처음으로 만나는 종료 위치는
-13입니다. 따라서 이 위치에 첫 번째 카메라를 설치합니다
그렇다면 현재 마지막 카메라 위치는 -13이 되며 이 구간은 카메라 확인이 완료되었으므로
다음 구간인 [-14, -5]를 확인합니다
두 번째 카메라 배치
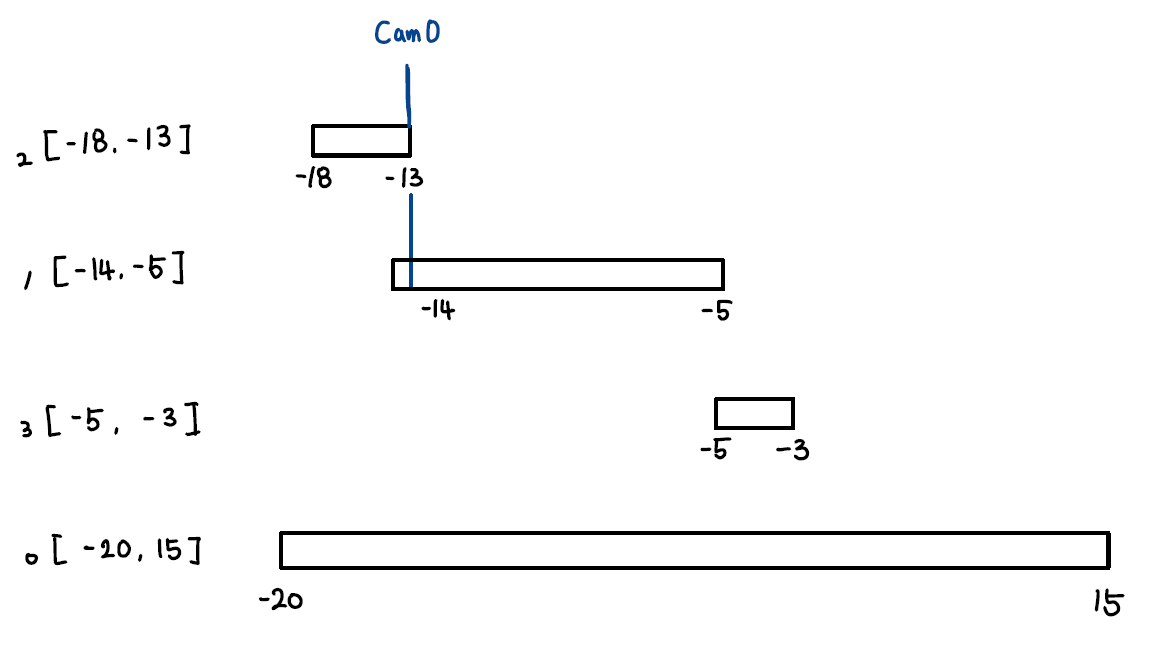
현재 카메라 위치는 -13이고, 두 번째 구간의 종료 위치는 -5입니다.
이제 이 구간의 시작 지점과 마지막 카메라의 위치를 비교합니다.
마지막 카메라 위치는 -13이었는데 이 구간의 시작 지점은 -14입니다.
따라서 이미 카메라를 한 번 만났으므로 이 구간에서는 새로 카메라를 설치할
필요가 없습니다.
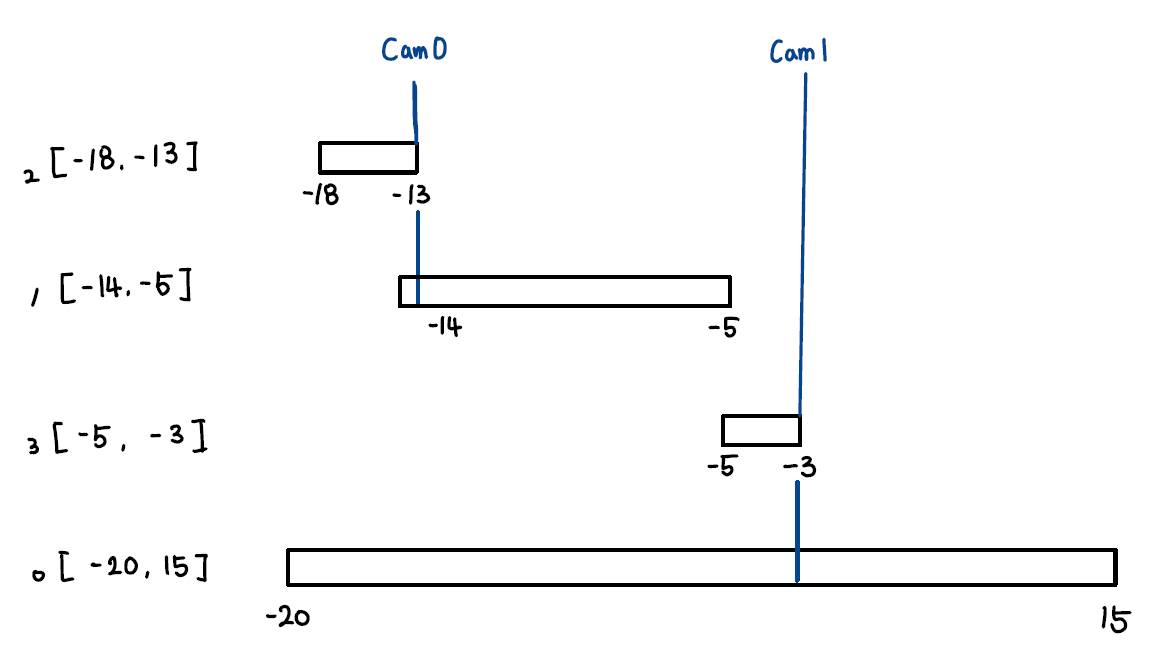
이제 다음 구간인 [-5, -3] 입니다. 아직도 카메라 위치는 -13이므로
이 구간에서 종료 지점에 새로운 카메라를 설치합니다.
이렇게 두 개의 카메라를 설치하면 다음 구간인 [-20, 15]는 마지막 위치의
-3 카메라가 있으므로 새로 설치할 필요가 없습니다.
정리
보통의 알고리즘 문제는 풀이 방법 자체를 떠올리는데 고민을 하지만
이 문제를 비롯한 그리디 문제들은 특이하게 직관적, 시각적으로는 이해가 쉬운 경우가 있지만
그 풀이들을 코드로 옮기는 과정이 어려운 경우가 많은 것 같습니다.
이 문제도 거기서 난항을 겪어 시간 내에 풀지 못해 검색을 통해 해결한 문제..
다음에 다시 한 번 풀어봐야할거같습니다 😜

문제 예시에서는 [-20, -15] 까지네요. 그림으로 엄청 자세히 설명해주셔서 잘 봤는데 잘못보신거같은... 전 첨에 풀려고 시도했을 때 정렬을 했는데 x기준으로 정렬 + y기준으로 정렬해서 그런지 틀렸다 나오더라고요. 그래서 음 뭐지 하면서 구글링했는데 글쎄 x기준 정렬은 굳이 안해도 되네요. 생각해보니 되게 단순한 원리 ㅎㅎ.. ㅠㅠ