Heap Sort

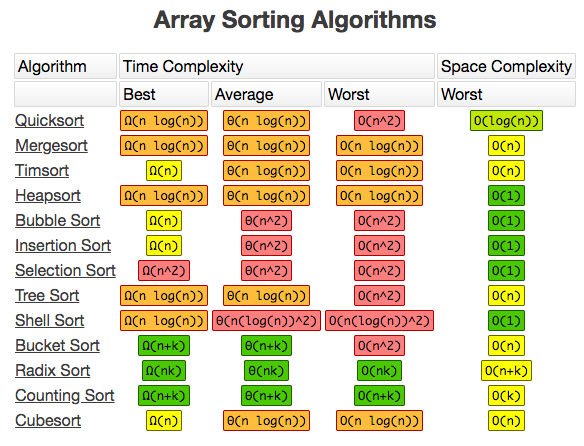
출처 : https://www.bigocheatsheet.com/

❓ Heap Sort란?

// Max Heap
void Heapify(int *arr, int N ,int i){
    int largest = i;
    int left = 2*i+1;  
    int right = 2*i+2;

    if(left < N && arr[left] > arr[largest])
        largest = left;

    if(right < N && arr[right] > arr[largest])
        largest = right;

    if(largest != i){
        swap(arr[i], arr[largest]);

        Heapify(arr, N, largest);
    }
}

void Heap_Sort(int *arr, int N){

    for(int i= N/2 -1;i>=0;i--){
        Heapify(arr, N, i);
    }

    for(int i = N-1; i>0; i--){
        swap(arr[0], arr[i]);

        Heapify(arr, i, 0);
    }
}

int main(){
    int arr[10] = {1,7,3,5,4,50,24,8,9,6};
    int N = sizeof(arr) / sizeof(arr[0]);

    Heap_Sort(arr, N);

    for(int i=0;i<10;i++){
        cout << arr[i] << " ";
    }
}

부모 노드의 수가 자식 노드의 수보다 큰 것을 이용한 정렬
1. 주어진 배열을 Max Heap으로 만들고, root노드의 수가 남은 배열 중에 가장 큰 수이므로 뽑아내기
2. 뽑아내며 망가진 Heap을 다시 Max Heap으로 만들기

Time Complexity : n(logn), n(logn), O(n(logn)) (Best, Average, Worst)
Space Complexity : O(1)

❓ Heap Sort는 언제 사용해야 할까?

이해하기 쉽고, 구현이 편하다.
시간복잡도 O(n(logn))에 공간 복잡도O(1)이므로 메모리 사용량을 최소화 하며, 대규모 데이터 일 때 좋은 성능을 유지한다.