이진탐색이란?

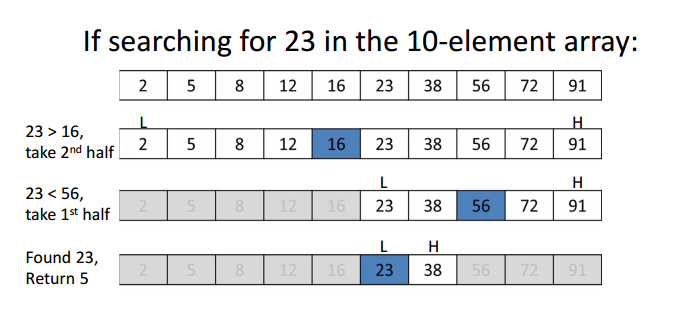
• 배열이 정렬되어있을 경우, 절반씩 줄여나가면서 탐색하는 기법

def binary_search(nums, target):
    def bs(start, end):
        if start > end:
            return -1

        mid = (start + end) // 2

        if nums[mid] < target:
            return bs(mid + 1, end)
        elif nums[mid] > target:
            return bs(start, mid - 1)
        else:
            return mid

    return bs(0, len(nums) - 1)


assert binary_search(nums=[-1, 0, 3, 5, 9, 12], target=9) == 4
assert binary_search(nums=[-1, 0, 3, 5, 9, 12], target=2) == -1

최단경로란?

그래프 이론에서 최단 경로 문제란 가장 짧은 경로에서 두 꼭짓점을 찾는 문제로서, 가중 그래프에서는 구성하는 변들의 가중치 합이 최소가 되도록 하는 경로

import heapq


def dijkstra_pq(graph, start):
    N = len(graph)
    dist = [INF] * N

    q = []
    # 튜플일 경우 0번째 요소 기준으로 최소 힙 구조.
    # 첫 번째 방문 누적 비용은 0이다.
    heapq.heappush(q, (0, start))
    dist[start] = 0

    while q:
        # 누적 비용이 가장 작은 녀석을 꺼낸다.
        acc, cur = heapq.heappop(q)

        # 이미 답이 될 가망이 없다.
        if dist[cur] < acc:
            continue

        # 인접 노드를 차례대로 살펴보며 거리를 업데이트한다.
        for adj, d in graph[cur]:
            cost = acc + d
            if cost < dist[adj]:
                dist[adj] = cost
                heapq.heappush(q, (cost, adj))

    return dist

import sys

from min_cost.dijkstra import dijkstra_naive, dijkstra_pq

with open('testcase1.txt') as f:
    sys.stdin = f
    input = sys.stdin.readline
    n, m = map(int, input().split())
    start = int(input())
    graph = [[] for _ in range(n + 1)]

    for _ in range(m):
        a, b, c = map(int, input().split())
        graph[a].append((b, c))

assert dijkstra_naive(graph, start) == [1000000000, 0, 2, 3, 1, 2, 4]
assert dijkstra_pq(graph, start) == [1000000000, 0, 2, 3, 1, 2, 4]