선택 정렬 (Selection Sort)

정의

---

• 리스트에 원소를 넣을 위치를 미리 정해두고, 어떤 원소를 넣을지 선택하는 알고리즘
• 거품 정렬(Bubble Sort)과 유사하다

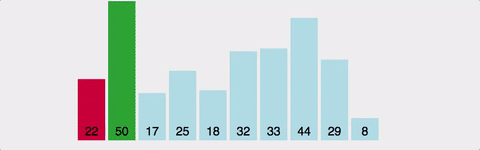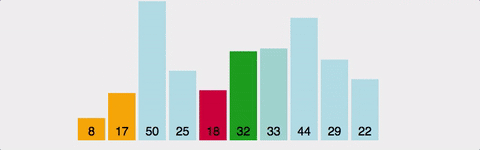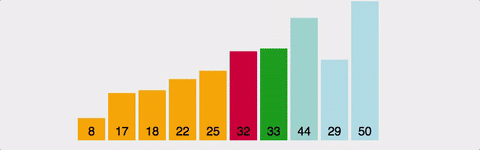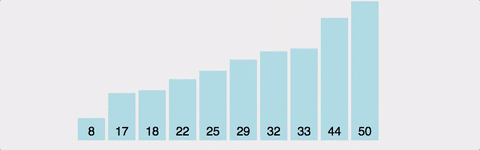
과정 (오름차순)

---

1. 주어진 리스트에서 최소값인 요소를 찾는다
2. 그 요소를 맨 앞의 요소와 교체한다
3. 맨 앞의 요소를 제외하고 같은 과정을 반복한다

코드 (JS)

---

const selectionSort = (arr) => {
  let indexMin, temp;
  for (let i = 0; i < arr.length - 1; i++) {
    indexMin = i;
    for (let j = i + 1; j < arr.length; j++) {
      if (arr[j] < arr[indexMin]) {
        indexMin = j;
      }
    }
    temp = arr[i];
    arr[i] = arr[indexMin];
    arr[indexMin] = temp;
  }
  console.log(arr);
};

시간 복잡도

---

• 비교 횟수
  최악, 평균, 최선 모두: (n-1) + (n-2) + ... + 2 + 1 = n(n-1) / 2
• 교환 횟수
  회당 한 번씩만 일어나므로 n - 1
• 따라서 T(n) = O(n^2)
• 매개변수가 정렬이 되었는지와 상관없이 무조건 비교하므로 최악, 평균, 최선 모두 동일

공간 복잡도

---

주어진 배열 안에서 교환(swap)을 통해 정렬되므로 O(n)

장점

---

• 거품 정렬과 마찬가지로 직관적이고 단순하다
• 거품 정렬처럼 비교 횟수는 많지만 교환 횟수는 적기에 교환이 많이 일어날 수 있는 자료 상태에서 효율적이다
• 제자리 정렬이다

단점

---

• 시간 복잡도가 O(n^2)로 비효율적이다
• 불안정 정렬이다

마무리

---

• 거품 정렬(Bubble Sort)과 유사하지만, 교환 횟수가 적어 좀 더 효율적이다

참조

• https://github.com/GimunLee/tech-refrigerator/blob/master/Algorithm/%EC%84%A0%ED%83%9D%20%EC%A0%95%EB%A0%AC%20(Selection%20Sort).md
• https://github.com/JaeYeopHan/Interview_Question_for_Beginner/tree/master/Algorithm
• https://jinhyy.tistory.com/9