정의
- 분할 정복(Divide and conquer)기법을 사용하는 정렬 알고리즘
- 정렬 기법 중 가장 빠르다고 해서 Quick이라는 이름이 붙여졌다
- real world 데이터에서 가장 빨라 많은 프로그래밍 언어들의 배열.sort() 메소드의 내부 구현에 사용된다
- 최악의 경우(e.g 정렬된 배열) 시간 복잡도가 O(n^2)이다
과정 (오름차순)
- 주어진 리스트에서 기준이 될 요소를 고른다. 이를 피벗(pivot)이라 한다
- 피벗을 기준으로 왼쪽은 피벗보다 작은 수가, 오른쪽은 큰 수가 오도록 정렬하여 리스트를 둘로 나눈다. 이 과정을 분할(Divide)이라 한다
- 분할을 마친 뒤 피벗은 더 이상 움직이지 않으며, 정렬 대상에서 제외된다
- 분할된 왼쪽, 오른쪽 리스트에 재귀적으로 위 과정을 반복한다(Conquer)
- 재귀 호출 1회당 최소 1개 피벗의 최종 위치가 정해지기에 재귀 호출의 종료가 보장된다
예시 (오름차순)
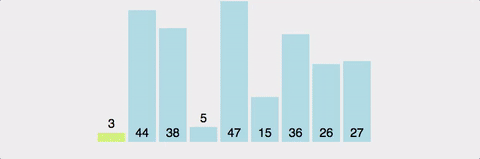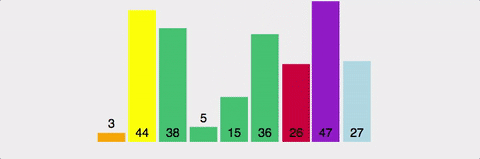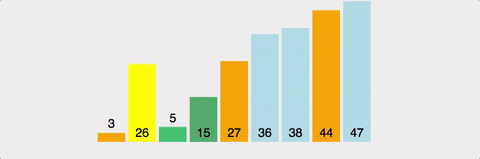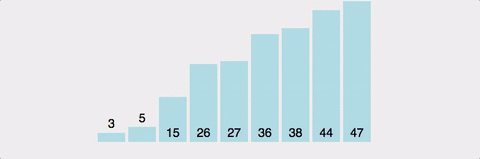
- [8, 1, 4, 2, 9, 3, 7, 6] 피벗을 고릅니다. 맨 뒤의 값인 6을 피벗으로 골랐습니다
- [8, 1, 4, 2, 9, 3, 7, 6] 6을 제외한 가장 왼쪽 값을 left, 오른쪽 값을 right로 정합니다. 이제 left를 오른쪽, right를 왼쪽으로 좁혀나가며 일련의 동작을 반복적으로 수행합니다.
left는 6보다 크면 제자리에 멈추고, 같거나 작으면 다음으로 넘어갑니다.
right는 6보다 작으면 제자리에 멈추고, 같거나 작으면 다음으로 넘어갑니다. - [8, 1, 4, 2, 9, 3, 7, 6] 따라서 8은 6보다 크니 멈추고, 7은 6보다 크니 넘어갑니다.
- [8, 1, 4, 2, 9, 3, 7, 6] 8은 6보다 크고 3은 6보다 작습니다. 이 때 둘을 교환하고 한 칸씩 좁혀 다음으로 넘어갑니다.
- [3, 1, 4, 2, 9, 8, 7, 6] 1은 6보다 작으니 넘어가고, 9는 6보다 크니 넘어갑니다.
- [3, 1, 4, 2, 9, 8, 7, 6] 4는 6보다 작으니 넘어가고, 2는 6보다 작으니 멈춥니다.
- [3, 1, 4, 2, 9, 8, 7, 6] 둘이 만났습니다. left의 2는 6보다 작으니 넘어갑니다. right의 2는 여전히 기다립니다.
- [3, 1, 4, 2, 9, 8, 7, 6] left의 9는 6보다 크니까 이제 left와 right를 교환해야 합니다. 그러나 left의 인덱스가 right보다 커졌을 때 left와 right의 교환은 이루어지지 않습니다. 대신 left와 피벗의 교환이 이루어집니다.
- [3, 1, 4, 2, 6, 8, 7, 9] 이제 왼쪽에는 6보다 작은 수, 오른쪽에는 6보다 큰 수들만 남았습니다. 여기까지가 Divide입니다.
- [3, 1, 4, 2, 6, 8, 7, 9] 아직 한 발 남았습니다.
6을 제외한 왼쪽의 [3, 1, 4, 2]와 오른쪽의 [8, 7, 9]에 퀵 정렬 함수를 재귀적으로 호출(Conquer)합니다.
이렇게 재귀로 스택을 쌓고 하나씩 쳐내다보면 정렬이 완료됩니다.
위 예시에서 왼쪽의 [3, 1, 4, 2]는 [1, 2, 4, 3]으로 한 차례 정렬된 후 [1, 2, 3, 4]로 정렬되고, 오른쪽의 [8, 7, 9]는 피벗인 9의 셀프 교환이 한 번 일어난 후 7로 피벗이 변경되어 7,8이 교환됨으로써 [7, 8, 9]로 정렬됩니다.
코드 (JS)
const partition = (array, left, right, pivotIndex) => {
let temp;
let pivot = array[pivotIndex];
while (left <= right) {
while (array[left] < pivot) {
left++;
}
while (array[right] > pivot) {
right--;
}
if (left <= right) {
temp = array[left];
array[left] = array[right];
array[right] = temp;
left++;
right--;
}
}
temp = array[left];
array[left] = pivot;
array[pivotIndex] = temp;
return left;
};
const quickSort = (array, left = 0, right = array.length - 1) => {
let pivotIndex = right;
pivotIndex = partition(array, left, pivotIndex - 1, pivotIndex);
if (left < pivotIndex - 1) {
quickSort(array, left, pivotIndex - 1);
}
if (right > pivotIndex + 1) {
quickSort(array, pivotIndex + 1, right);
}
return array;
};
시간 복잡도
- 최악 (이미 오름차순, 혹은 내림차순으로 정렬된 경우)
- 재귀 호출의 깊이(k)
- 레코드의 개수를 n이라 한다.
- 이 때, 이미 정렬된 경우라면 partition의 결과 한 쪽은 계속 비고, 한 쪽은 계속 꽉 차게 된다.
- 그래서 재귀 호출도 한 쪽만 작동하게 된다.
- 따라서 재귀 호출의 깊이는 레코드의 개수 n이 된다.
- 각 재귀 호출에서의 비교 횟수
- 대부분의 레코드를 비교해야 하기에 평균 n번 정도의 비교가 이루어진다. (교환 횟수는 비교 횟수보다 적으므로 무시할 수 있다)
- 결론
T(n) = 재귀 호출의 깊이 x 각 재귀 호출에서의 비교 횟수 = n x n
따라서 시간 복잡도는 O(n^2)
- 재귀 호출의 깊이(k)
- 최선, 평균
- 재귀 호출의 깊이(k)
- 레코드의 개수를 n이라 하고, n이 2의 거듭제곱이라 가정한다. (n = 2^k)
- n=2^3일 때 2^3 -> 2^2 -> 2^1 -> 2^0으로 줄어들어 재귀 호출의 깊이가 3임을 알 수 있다.
- 이를 일반화하면 재귀 호출의 깊이 k = log₂n임을 알 수 있다.
- 각 재귀 호출에서의 비교 횟수
- 대부분의 레코드를 비교해야 하기에 평균 n번 정도의 비교가 이루어진다.
(교환 횟수는 비교 횟수보다 적으므로 무시할 수 있다)
- 대부분의 레코드를 비교해야 하기에 평균 n번 정도의 비교가 이루어진다.
- 결론
T(n) = 재귀 호출의 깊이 x 각 재귀 호출에서의 비교 횟수 = n x log₂n
따라서 시간 복잡도는 O(nlog₂n)
- 재귀 호출의 깊이(k)
공간 복잡도
주어진 배열 안에서 교환(swap)을 통해 정렬되므로 O(n)
장점
- 불필요한 데이터 교환이 비교적 적게 일어난다
- 먼 거리의 데이터를 교환한다
- 한 번 위치가 결정된 피벗들은 추후 연산에서 제외된다
- 위와 같은 특성들로 인해서 같은 nlog₂n의 시간 복잡도를 가지는 다른 정렬 알고리즘들과 비교해도 가장 빠르다
- 제자리 정렬이다
단점
- 정렬된 리스트에서는 불균형 분할로 인해 더 많은 시간이 걸린다
- 불안정 정렬이다
마무리
- real-world 데이터에서 평균적으로 가장 빠른 정렬 알고리즘으로 빈번하게 사용되니 꼭 알아두자.